Hongaarse methode Wat bestaat, voorbeeld

Hij Hongaarse methode Het is een algoritme dat wordt gebruikt in toewijzingsproblemen wanneer u de kosten wilt minimaliseren. Dat wil zeggen, het wordt gebruikt om de minimale kosten te vinden door verschillende mensen toe te wijzen aan verschillende activiteiten op basis van de laagste kosten. Elke activiteit moet aan een andere persoon worden toegewezen.

Een probleem van toewijzing is een speciaal type lineair programmeringsprobleem, waarbij het doel is om de kosten of tijd van het voltooien van een hoeveelheid werk van verschillende mensen te minimaliseren.

Bron: Pixabay.com

Een van de belangrijke kenmerken van het toewijzingsprobleem is dat slechts één werk (of werknemer) wordt toegewezen aan een machine (of project).

Deze methode is ontwikkeld door de Hongaarse wiskundige D. Konig. Om deze reden staat het bekend als de Hongaarse methode voor toewijzingsproblemen. Het is ook bekend als Kuhn-Munkres-toewijzingsalgoritme.

Elk toewijzingsprobleem kan eenvoudig worden opgelost door deze methode toe te passen die uit twee fasen bestaat:

- Met de eerste fase zijn er reducties van rijen en kolomverminderingen.

- In de tweede fase is de oplossing op een iteratieve basis geoptimaliseerd.

[TOC]

Wat is de Hongaarse methode?

De Hongaarse methode bestaat uit vier stappen. De eerste twee stappen worden slechts eenmaal uitgevoerd, terwijl stappen 3 en 4 worden herhaald totdat ze een optimale opdracht vinden.

Het wordt beschouwd als toegangsfeit voor een vierkante matrix van orde n door n, die alleen niet -negatieve elementen moet bevatten.

Voor een bepaald probleem, als het aantal rijen in de matrix niet gelijk is aan het aantal kolommen, moet een fictieve rij of een fictieve kolom worden toegevoegd, afhankelijk van de zaak. Toewijzingskosten voor deze fictieve cellen worden altijd toegewezen als nul.

Stap 1: Trek de minima van elke rij af

Voor elke rij van de matrix wordt het element geselecteerd met de laagste waarde en aftrekkingen van elk element in die rij.

Kan u van dienst zijn: wat is het huidige troef? (Met voorbeelden)

Stap 2: Trek de minima van elke kolom af

Evenzo wordt het element met de laagste waarde voor elke kolom geselecteerd en het aftrekt van elk element in die kolom.

Stap 3: Bedek alle nullen met een minimum aantal regels

Alle nullen moeten worden bedekt met de matrix als gevolg van stap 2 met behulp van een minimum aantal horizontale en verticale lijnen, hetzij door rijen of kolommen.

Als een totale lijnen nodig zijn om alle nullen te bedekken, is er gelijk aan de grootte n per n van de matrix, er is een optimale toewijzing tussen de nullen en daarom stopt het algoritme.

Anders, als er minder lijnen nodig zijn om alle nullen in de matrix te bedekken, gaat het door met stap 4.

Stap 4: Creëer extra nullen

Het minste element van de matrix (K) wordt geselecteerd dat niet wordt behandeld door een van de lijnen die zijn gemaakt in stap 3.

De waarde van k van alle elementen die niet door lijnen vallen, wordt afgetrokken. Vervolgens wordt de waarde van K toegevoegd aan alle elementen die worden gedekt door de kruising van twee lijnen.

De elementen die door een enkele lijn vallen, blijven zoals ze zijn. Na het uitvoeren van deze stap keert u terug naar stap 3.

Optimale opdracht

Zodra het algoritme is gestopt in stap 3, wordt een set nullen gekozen zodat elke rij en elke kolom slechts één geselecteerde nul heeft.

Als er in dit selectieproces geen enkele nul in een rij of kolom is, wordt een van die nullen gekozen. De resterende nullen worden geëlimineerd in die kolom of rij, en herhalen hetzelfde voor de andere opdrachten ook.

Het kan u van dienst zijn: macrolocalisatie

Als er geen enkele toewijzing van nullen is, betekent er dat er meerdere oplossingen zijn. De kosten blijven echter hetzelfde voor de verschillende toewijzingssets.

Elke fictieve rij of kolom die is toegevoegd, wordt geëlimineerd. De in deze uiteindelijke matrix gekozen nullen komen overeen met de ideale toewijzing die vereist is in de originele matrix.

Voorbeeld

Overweeg een bedrijf waar vier activiteiten zijn (A1, A2, A3, A4) die moeten worden uitgevoerd door vier werknemers (T1, T2, T3, T4). Een activiteit per werknemer moet worden toegewezen.

De volgende matrix toont de kosten voor het toewijzen van een bepaalde werknemer aan een bepaalde activiteit. De doelstelling is om de totale kosten van de taak uit deze vier activiteiten te minimaliseren.

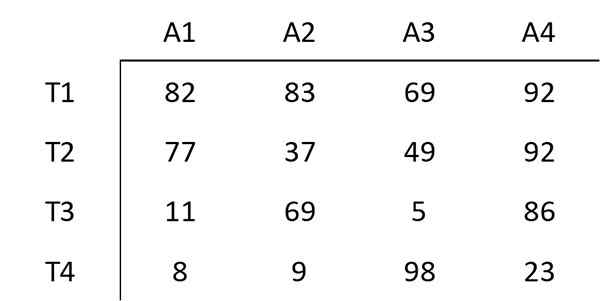
Stap 1: Trek de minima van elke rij af

Het element begint met de minimale waarde van elke rij van de andere elementen van die rij. Het kleinste element in de eerste rij is bijvoorbeeld 69. Daarom wordt 69 van elk element op de eerste rij afgetrokken. De resulterende matrix is:

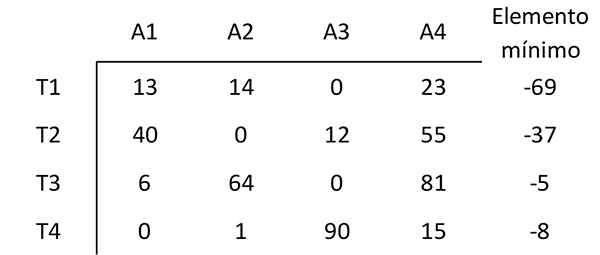
Stap 2: Trek de minima van elke kolom af

Op dezelfde manier wordt het element afgetrokken met de minimale waarde van elke kolom van de andere elementen van die kolom, waarbij de volgende matrix wordt verkregen:

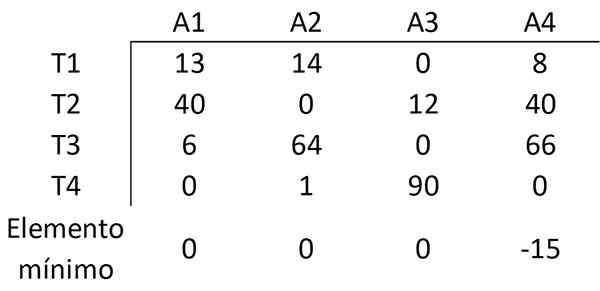
Stap 3: Bedek alle nullen met een minimum aantal regels

Nu wordt het minimale aantal lijnen (horizontaal of verticaal) bepaald dat nodig is om alle nullen in de matrix te bedekken. Alle nullen kunnen worden behandeld met 3 lijnen:

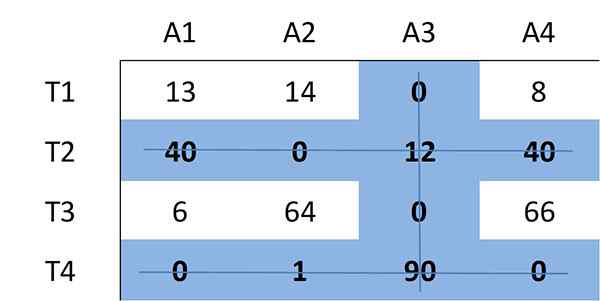
Omdat het aantal vereiste lijnen drie is en minder is dan de grootte van de matrix (n = 4), gaat het door met stap 4.

Kan u van dienst zijn: Projectbeheer: wat is, fasen, doelstellingen, voorbeelden

Stap 4: Creëer extra nullen

Het laagste element dat niet door de lijnen wordt bedekt, is geselecteerd, waarvan de waarde 6 is. Deze waarde van alle niet -bedekte elementen wordt afgetrokken en deze zelfde waarde wordt toegevoegd aan alle elementen die onder de kruising van twee lijnen vallen. Dit resulteert in de volgende matrix:

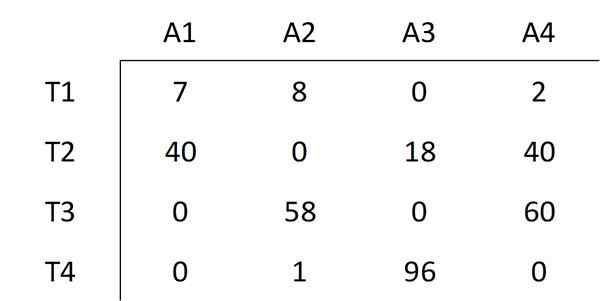
Zoals aangegeven in de Hongaarse methode, moet de stap nummer drie opnieuw worden uitgevoerd.

Stap 3 (herhaling)

Nogmaals, het minimale aantal lijnen dat nodig is om alle nullen in de matrix te bedekken, wordt bepaald. Deze keer zijn vier regels vereist:

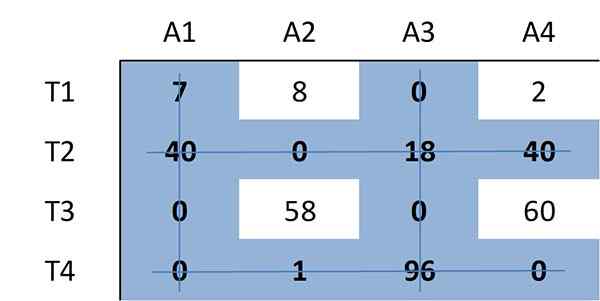
Omdat het aantal benodigde lijnen 4 is, gelijk aan de grootte van de matrix (n = 4), is er een optimale toewijzing tussen nullen in de matrix. Daarom stopt het algoritme.

Optimale opdracht

Zoals aangegeven door de methode, komt de selectie van de volgende nullen overeen met een optimale opdracht:

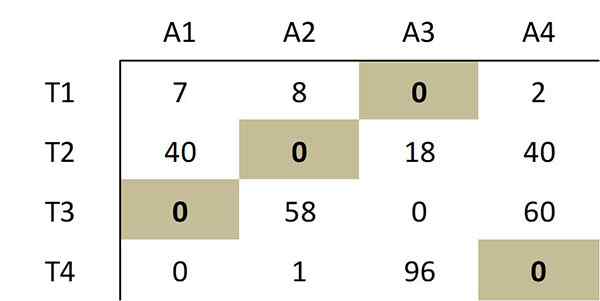
Deze selectie nullen komt overeen met de volgende optimale toewijzing in de oorspronkelijke kostenmatrix:

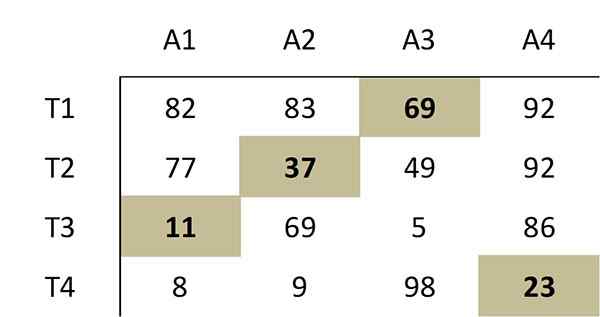
Daarom moet de werknemer 1 activiteit 3, de werknemer 2, de activiteit 2, de werknemer 3, de activiteit 1 en de werknemer 4 uitvoeren, moeten de activiteit uitwerken 4. De totale kosten van deze optimale toewijzing zijn 69+37+11+23 = 140.

Referenties

1. Hongarije algoritme (2019). Het Hongarije -algoritme. Genomen uit: Hongaarsealgorithm.com.
2. Studie (2019). Het gebruik van het Hongarije -algoritme om opdrachtproblemen op te lossen. Genomen van: Studie.com.
3. Wisdom Jobs (2018). Hongarije methode voor het oplossen van toewijzingsprobleem - Kwantitatieve technieken voor management. Uitgevoerd uit: WisdomJobs.com.
4. Geeks voor geeks (2019). Hongarije algoritme voor toewijzingsprobleem. Genomen uit: geeksforgeeks.borg.
5. Karleight Moore, Nathan Landman (2019). Hongarije maximaal matching -algoritme. Briljant. Uitgebracht van: briljant.borg.