Uniforme cirkelvormige beweging (m.C.OF.) Formules, kenmerken

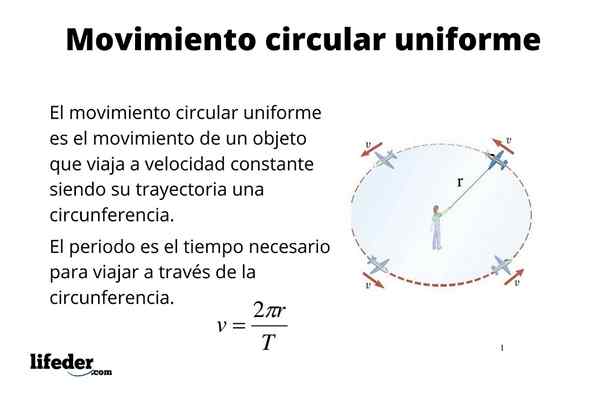
Een deeltje heeft cirkelvormige beweging uniform (M.C.OF.) Wanneer het traject ervan een omtrek is en er ook constant door reist. Talrijke objecten zoals stukken machines en motoren hebben bijvoorbeeld dit soort beweging, waaronder de harde schijven van de computers, de fenaters, bijlen en nog veel meer dingen zijn meer.

De uniforme cirkelvormige beweging is ook een goede benadering van de beweging van sommige hemelse lichamen zoals de aarde. De baan van de aarde is echt elliptisch, zoals de wetten van Kepler erop wijzen. De excentriciteit van de baan is echter klein en als een eerste benadering kan deze worden beschouwd als circulair, wat enkele berekeningen vereenvoudigt, zoals het vinden van de snelheid van de aarde wanneer deze rond de zon beweegt.

In de beschrijving van de uniforme cirkelvormige beweging worden dezelfde parameters gebruikt als in de rechtlijnige beweging, namelijk: positie, verplaatsing, tijd, snelheid en versnelling.

Versnelling? Ja, in feite wordt de uniforme cirkelvormige beweging versneld, zelfs wanneer de snelheid zijn v constant zijn. Dit komt omdat de snelheid v, Dat het een vector is en daarom is het vetgedrukt, het verandert voortdurend van richting terwijl het object of deeltje roteert. Elke verandering in v Het wordt geproduceerd door een versnelling, die zoals het zal worden gezien, is gericht op het midden van het cirkelvormige traject.

De uniforme cirkelvormige beweging is een beweging in het vlak XY, Daarom is het een twee -dimensionale beweging. Het is echter mogelijk om het comfortabeler uit te drukken door de hoek θ die het deeltje veegt, gemeten met betrekking tot de horizontale as of andere geschikte referentieas.

Zelfs als het een uitgebreid object is, vegen de deeltjes altijd dezelfde hoek, zelfs als ze verschillende coördinaten hebben (X, y).

[TOC]

Kenmerken van uniforme cirkelvormige beweging

U kunt de kenmerken van de uniforme cirkelvormige beweging als volgt samenvatten:

-Het traject is een omtrek, daarom is het een beweging in het vlak.

-De snelheid v Het is constant, maar de snelheid v Nee, omdat het voortdurend van richting en de betekenis verandert om de beurt van de mobiel te accommoderen.

-De snelheidsvector v Het is altijd tangentieel voor de omtrek en loodrecht op de radiale richting.

-Hoeksnelheid ω is constant.

-Ondanks dat het uniform is, is er een versnelling om deze veranderingen in de snelheidsrichting te verklaren. Deze versnelling is centripetale versnelling.

-Centripetale versnelling en snelheid staan ​​loodrecht op elkaar.

-Het is een periodieke of repetitieve beweging, daarom worden de grootte -periode en frequentie voor hem gedefinieerd.

Uniforme cirkelvormige bewegingsformules

In dit schema is er een P -deeltjes -spin v getrokken.

Kan u dienen: het magnetische veld van de aarde: oorsprong, kenmerken, functie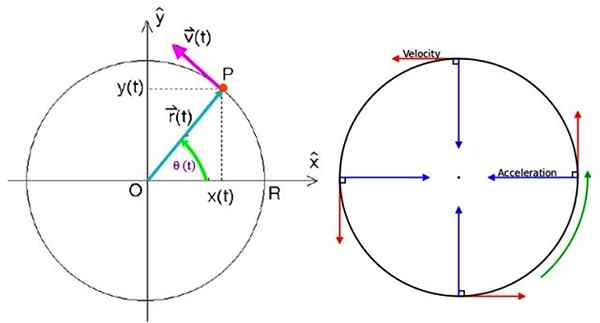 Uniforme circulaire bewegingsparameters. Bron: f. Zapata/Wikimedia Commons.

Om de positievector op te geven, is dit noodzakelijk.

Positievector

Het wordt aangeduid als r (t) en wordt gericht van de oorsprong tot het punt P waar het deeltje zich bevindt. In een moment gegeven T, in Cartesiaanse coördinaten, is het geschreven als:

R (t) = x (t) Je + en (t) J

Waar Je En J Ze zijn de loodrechte eenheidsvectoren in de aanwijzingen X En En respectievelijk. Van de grafiek wordt waargenomen dat de vectormodule R (t) Altijd oké R, De straal van de omtrek. Als θ de hoek is die zich vormt R Met de horizontale as is de positie ook gelijk aan:

R (t) = [rcos θ(T)] Je +[RSEN θ(T)] J

De hoek die zich vormt R (T) Met de horizontale as is het een centrale hoek en de waarde ervan is:

θ = s/r

Waar s de omtrekboog is afgelegd en de radio is. Zei hoek θ Het is een tijdfunctie, dus je kunt schrijven θ = θ (T), telefoongesprek hoekige positie.

Omdat de snelheid constant is, beschrijft het deeltje gelijke hoeken in gelijke tijden en in analogie met de uniforme rechtlijnige beweging, wordt geschreven:

θ = θ (t) = θ_of + ωt

Hier θ_of Het is de initiële hoek gemeten in radialen met betrekking tot de referentieas, het kan 0 of elke waarde zijn en ω is de hoeksnelheid.

Hoeksnelheid en lineaire snelheid

Hoeksnelheid is de eerste afgeleid van de hoekpositie en wordt aangeduid als ω. De waarde ervan is constant voor de uniforme cirkelvormige beweging, omdat gelijke hoeken in gelijke tijden schermen. Met andere woorden:

Hoeksnelheid komt in eenheden van radialen/s. Van zijn kant wordt de lineaire snelheid berekend door:

Lineaire snelheid is de module of grootte van de lineaire snelheid, die verandert naarmate het deeltje draait na het traject. De snelheidsrichting is dus het tangentiële adres van de omtrek.

De eenheden van de lineaire snelheid in de uniforme cirkelvormige beweging zijn hetzelfde als voor lineaire bewegingen: m/s (in het internationale systeem SI), km/u, cm/s en andere.

Centripetale versnelling

In de volgende figuur is er een deeltje dat beweegt in een schema van de omtrek met constante snelheid. Dit betekent dat de snelheidsvector altijd dezelfde module heeft, maar van richting verandert om de omtrek tegemoet te komen.

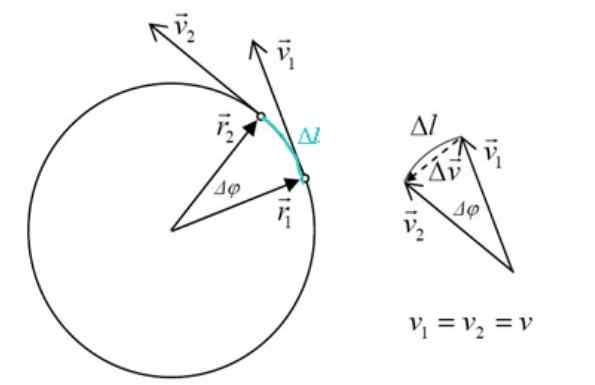Snelheid en versnelling in de uniforme cirkelvormige beweging. Bron: f. Zapata.

Elke verandering in snelheidsresultaten in een versnelling, wat per definitie is:

Kan u van dienst zijn: de 31 soorten kracht in de natuurkunde en hun kenmerken

In het bovenstaande beeld is de aftrekking tussen de vectoren v₂ En v₁, waarvan het resultaat δ isv, vector evenredig met versnelling. Zoals u kunt zien, wijst altijd naar het midden van de omtrek en daarom wordt het centripetale versnelling of radiale versnelling genoemd.

De driehoek gevormd door v₂, v₁ en δv Het is vergelijkbaar met de driehoek van de zijkanten R₂, R₁ en δl, Zijnde Δφ de centrale hoek. De magnitudes van R₂ En R₁ Ze zijn hetzelfde, dus:

R₂ = r₁ = r

Dan zijn beide driehoeken deze relaties voor de hoek:

Δφ = Δr / r; Δφ = ΔV / v

Vet is niet nodig, omdat de maat van de hoek afhangt van de grootte van deze vectoren. Equalisatie van de bovenstaande uitdrukkingen Hieruit volgt dat:

 Dus:

Deel aan beide zijden door AT, om de grootte van de versnelling te verkrijgen:

Maar Δr / Δt is de grootte van de snelheid, genoemd v, daarom:

Eindelijk is de centripetale versnelling:

Periode en frequentie

Omdat de circulaire beweging repetitief is, wordt de periode gedefinieerd T van hetzelfde als de tijd die de mobiel nodig heeft om een ​​complete beurt te nemen. Aangezien de lengte van de straal van straal R 2πr is, is de hoek geveegd in radianen wanneer het volledig draaien 2π radialen is en tijd t kost, is de hoeksnelheid:

Ω = 2π / t

T = 2π / ω

De periode van uniforme cirkelvormige beweging wordt gemeten in seconden in het internationale systeem.

Van zijn kant, de frequentie F Het is het aantal beurten per tijdseenheid en is de wederzijdse of omgekeerde van de periode:

F = n /t = 1 /t

De frequentie -eenheid in het internationale systeem is s^-1.

Uniforme circulaire bewegingsvoorbeelden

Veel objecten roteren om verschillende effecten te produceren: wielen, schijven en turbines. Zodra de besturingssnelheid is bereikt, wordt de rotatie meestal met constante snelheid uitgevoerd. De cirkelvormige beweging is zo gebruikelijk in het dagelijks leven dat je er bijna nooit aan denkt, dus hier zijn enkele nauwe voorbeelden die het heel goed illustreren:

De beweging van de aarde

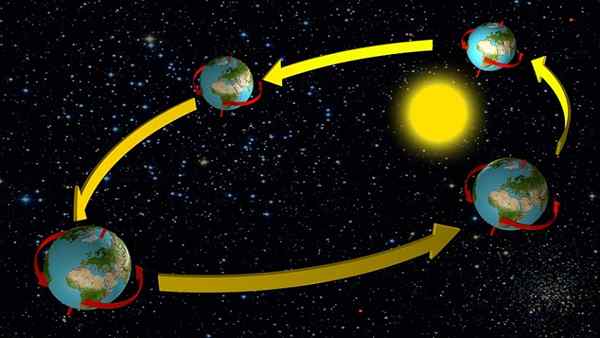
Aarde en andere planeten van het zonnestelsel bewegen in elliptische trajecten van kleine excentriciteit, behalve Mercurius, wat betekent dat in de eerste benadering kan worden aangenomen dat zijn beweging uniform circulair is.

Dit heeft een goed idee van de snelheid van vertaling rond de zon, omdat in het geval van de aarde de bewegingsperiode bekend is: een jaar of 365 dagen.

Deeltjes aan de rand van een album

De deeltjes die draaien aan de rand van een oude toadiscos of de rage van een ventilator, volgen een uniforme cirkelvormige beweging, zodra het apparaat zijn reproductiesnelheid bereikt.

Kan u van dienst zijn: Dirac Jordan Atomic Model: kenmerken en postulaten

Hubble Space Telescope

Hubble Space Telescope draait rond de aarde met ongeveer 7550 m/s.

Centrifugators

De wasmachines voeren een gecentrifugeerd proces uit om kleding te persen, die bestaat uit het roteren van de high speed container drum. De drogers draaien ook een tijdje met uniforme cirkelvormige beweging.

Centrifugatie wordt ook gebruikt in laboratoria om bijvoorbeeld verbindingen te scheiden, en scheiden zo de bestanddelen ervan door verschil in dichtheden. Wanneer er sprake is van centrifugeren, is er een cirkelvormige beweging die uniform is, althans voor een tijdje.

Tuinbuien

Veel tuinbuien draaien voortdurend naar het land om in een paar water te geven.

Sport

In de hamerlancering bijvoorbeeld, een Olympische discipline, draait de atleet een metalen bal met een stalen kabel die aan de handvat is bevestigd. Het doel is om de bal zo ver mogelijk te sturen, maar zonder een bepaald gebied te verlaten.

Oefening opgelost

Een deeltje beweegt in een straalcirkel van 2 m met een constante snelheid v = 8 m/s, in de tegenovergestelde richting van de klok. Aanvankelijk was het deeltje in R = +2 J M. Berekenen:

a) hoeksnelheid ω

b) zijn hoekpositie θ (t)

c) De periode van beweging

d) Centripetale versnelling.

e) Positie van het deeltje na het passeren van t = π/4 s

Oplossing voor

Uit de formule v = rΩ Het volgt dat:

Ω = v/r = (8 m/s)/2m = 4Rad ∙ s s^-1

Oplossing B

Als u als referentieas naar de positieve X -as neemt, bevindt het deeltje zich aanvankelijk op 90º = π/2 radialen met betrekking tot de genoemde as, omdat de verklaring zegt dat de beginpositie +2 is J m, dat wil zeggen, het deeltje is in y = 2m wanneer de beweging begint te volgen.

θ = θ (t) = θ_of + ωt = π/2 + 4t

Oplossing C

T = 2π / ω = 2π / 4 s = 0.5 π s

Oplossing D

A = V² / R = (8 m/ s)² / 2 m = 32 m/ s²

Oplossing e

θ (t) = π/2 + 4t → θ (π/4) = π/2 + 4 ∙ (π/4) = 3π/2 radialen

Dit betekent dat het deeltje na die tijd in positie Y = -2m staat J. Het is logisch omdat t = π/4 s de helft van de periode is, daarom heeft het deeltje een hoek van 180º in een anti -gehoorelijke zin gereden sinds de initiële positie en moet recht in de tegenovergestelde positie zijn.

Referenties

1. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Deel 1. Kinematica. Uitgegeven door Douglas Figueroa (USB).
2. Giambattista, een. 2010. Natuurkunde. 2e. ED. McGraw Hill.
3. Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14e. ED. Deel 1. Pearson.
4. Serway, r., Jewett, J. (2008). Natuurkunde voor wetenschap en engineering. Deel 1. 7e. ED. Cengage leren.
5. Zapata, f. Cirkelvormige beweging. Hersteld van: Francesphysics.Blogspot.com.