Torsiemoment

We leggen uit wat de tijd is van torsie, de kenmerken, formules, eenheden, toepassingen en oefeningen om op te lossen

Wat is de tijd van torsie?

Hij Torsiemoment, koppel of moment van kracht is het vermogen van een kracht om een ​​beurt te veroorzaken. Etymologisch wordt het koppel genoemd als een afleiding van het Engelse woord Koppel, van het Latijn Torquere (twist).

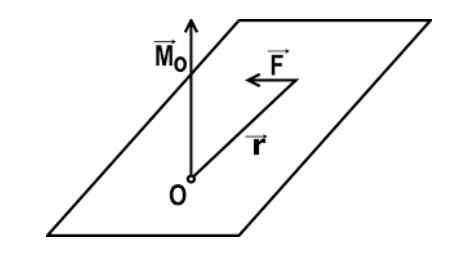
De tijd van torsie (ten opzichte van een bepaald punt) is de fysieke grootte die het gevolg is van het uitvoeren van het vectorproduct tussen de positievectoren van het punt waarop de kracht wordt uitgeoefend en die van de uitgeoefende kracht (in de aangegeven volgorde). Dit moment hangt af van drie hoofdelementen.

De eerste van deze elementen is de grootte van de uitgeoefende kracht, de tweede is de afstand tussen het punt waar het van toepassing is en het punt ten opzichte van het lichaam roteert (ook wel de hendelarm genoemd), en het derde element is de hoektoepassing van zei kracht.

Grotere kracht, grotere beurt wordt veroorzaakt. Hetzelfde geldt voor de hendelarm: hoe groter de afstand tussen het punt waarop de kracht en het punt worden uitgeoefend ten opzichte van die van de beurt, hoe groter dit zal zijn.

Logischerwijs is de tijd van torsie van bijzonder belang in de bouw en de industrie, evenals aanwezig in talloze thuistoepassingen, zoals wanneer een noot wordt geperst met een Engelse sleutel.

Formules

De wiskundige uitdrukking van het moment van torsie van een kracht ten opzichte van een punt of wordt gegeven door: m = r x f

In deze uitdrukking is r de vector die het punt van O verenigt met de punt P van de toepassing van de kracht, en F is de vector van de uitgeoefende kracht.

Kan u van dienst zijn: elektrodynamica

De eenheden van de maatregel van het moment zijn N ∙ M, wat, hoewel dimensionaal equivalent aan juli (J), een andere betekenis heeft en niet in de war moet worden.

Daarom neemt de koppelmomentmodule de waarde aan die wordt gegeven door de volgende uitdrukking:

M = r ∙ f ∙ Sen α

In deze uitdrukking is α de hoek tussen de sterkte vector en de vector R of hendelarm. De tijd van torsie wordt als positief beschouwd als het lichaam in de tegenovergestelde richting van de kloknaalden draait; Integendeel, het is negatief als het in een schema verandert.

Eenheden

De meeteenheid van de torsie is het product van een krachteenheid door een afstandseenheid. In het bijzonder wordt in het internationale systeem van eenheden de Newton Metro gebruikt waarvan het symbool is n • m is.

Op het dimensionale niveau lijkt de Newton Metro mogelijk gelijkwaardig aan juli; In geen enkel geval mag juli worden gebruikt om momenten uit te drukken. Juli is een eenheid om werken of energieën te meten die, vanuit een conceptueel oogpunt, heel anders zijn dan torsiemomenten.

Evenzo presenteert het moment van torsie een vectorkarakter, dat zowel werk als schaalsenergie is.

Torsiemomentkenmerken

Uit het gezien volgt het dat het moment van torsie van een kracht ten opzichte van een punt het vermogen van een kracht of set krachten vertegenwoordigt om de rotatie van het lichaam rond een as te wijzigen die door het punt gaat.

Daarom genereert het moment van torsie een hoekige versnelling op het lichaam en is het een grootte van een vectorpersonage (dus wordt het gedefinieerd uit een module, een richting en een gevoel) die aanwezig is in de mechanismen die zijn onderworpen aan torsie of flexie.

Het kan u van dienst zijn: Vy Canis Majoris: Discovery, Kenmerken, Structuur, Training en Evolutie

De tijd van torsie zal nietig zijn als de sterkte vector en vector R dezelfde richting hebben, omdat in dat geval de waarde van sen α nietig zal zijn.

Resulterend koppel

Gegeven een bepaald lichaam waarop een serie krachten werkt, als de toegepaste krachten in hetzelfde vlak werken, het moment van torsie dat het gevolg is van de toepassing van al deze krachten; Het is de som van de torsiemomenten als gevolg van elke kracht. Daarom is het vervuld dat:

M_T = ∑ m = m₁ + M_{2 +} M₃ +..

Het is natuurlijk noodzakelijk om rekening te houden met het criterium van tekenen voor torsiemomenten, zoals hierboven uitgelegd.

Toepassingen

Het koppel is aanwezig in toepassingen zo elke dag als het knijpen van een moer met een Engelse sleutel, of het openen of sluiten van een tik of een deur.

Uw toepassingen gaan echter veel verder; De tijd van torsie wordt ook gevonden in de assen van de machines of in het resultaat van de inspanningen waaraan de stralen worden onderworpen. Daarom zijn de toepassingen in de industrie en mechanica veel en gevarieerd.

Opgeloste oefeningen

Hieronder staan ​​een paar oefeningen om het begrip van het bovenstaande te vergemakkelijken.

Oefening 1

Gegeven de volgende figuur waarin de afstanden tussen punt O en punten A en B respectievelijk 10 cm en 20 cm zijn:

a) Bereken de waarde van de koppelmodule ten opzichte van het punt of als een kracht van 20 n wordt toegepast op punt A.

b) Bereken wat de waarde van de kracht moet zijn die in B wordt toegepast om dezelfde tijd van torsie te bereiken die in de vorige sectie werd verkregen.

Kan u van dienst zijn: continuïteitsvergelijking

Oplossing

Ten eerste moeten gegevens naar internationale systeemeenheden slagen.

R_NAAR = 0,1 m

R_B = 0,2 m

a) Om het torsiemoment te berekenen, gebruiken we de volgende formule:

M = r ∙ f ∙ Sen α = 0,1 ∙ 20 ∙ 1 = 2 n ∙ m m

b) Om de gevraagde kracht te bepalen, ga je op een vergelijkbare manier verder:

M = r ∙ f ∙ Sen α = 0,2 ∙ f ∙ 1 = 2 n ∙ m m

Het opruimen van het is verkregen dat:

F = 10 n

Oefening 2

Een vrouw voert een kracht van 20 n uit aan het einde van een Engelse sleutel van 30 cm lang. Als de hoek van de kracht met de sleutel van de sleutel 30 ° is, wat is dan de tijd van draai in de moer?

Oplossing

De volgende formule wordt toegepast en werkt:

M = r ∙ f ∙ Sen α = 0,3 ∙ 20 ∙ 0,5 = 3 n ∙ m m