Bohr Atomic Model

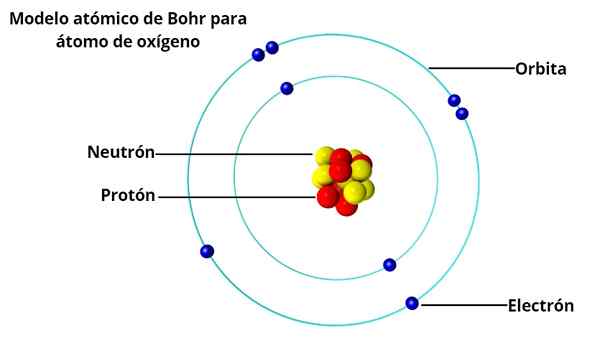
Hij Bohr Atomic Model Het is de opvatting van de Deense fysicus Niels Bohr (1885-1962) over de structuur van het atoom, gepubliceerd in 1913. In het Bohr -atoom bezetten elektronen rond de kern alleen bepaalde toegestane banen, dankzij een beperking genaamd kwantificering.

Voor Bohr, het beeld van het atoom als een miniatuur zonnestelsel, met elektronen door rond de kern rond te draaien, was het niet volledig consistent met het feit dat elektrische ladingen, wanneer ze worden versneld, stralen energie uit.

Zo'n atoom zou niet stabiel zijn, omdat het zou eindigen om vroeg of laat in te storten omdat de elektronen spiraalvormig naar de kern zouden neerslaan. En tegen die tijd, 50 jaar geleden de karakteristieke lichtpatronen die waterstof en andere gassen uitzenden tijdens het verwarmen.

Het patroon of het spectrum bestaat uit een reeks heldere lijnen van bepaalde zeer specifieke golflengten. En het waterstofatoom stort niet in door licht uit te zenden.

Om uit te leggen waarom het atoom stabiel is ondanks dat het in staat is elektromagnetische energie te kunnen uitstralen, stelde Bohr voor dat het hoekmomentum alleen bepaalde waarden kon aannemen, en dus ook de energie. Dit is wat wordt begrepen door kwantisatie.

Het aanvaarden dat de energie werd gekwantiseerd, zou het elektron de nodige stabiliteit hebben om niet naar de kern te rennen die de atoom vernietigt.

En het atoom straalt alleen lichte energie uit wanneer het elektron overgangen van de ene baan naar de andere maakt, altijd in discrete hoeveelheden. Op deze manier wordt de aanwezigheid van emissiepatronen in waterstof uitgelegd.

Bohr samengesteld op deze manier een visie van het atoom dat bekende concepten van klassieke mechanica integreerde met de nieuw ontdekte, zoals de constante van Planck, het foton, het elektron, de atomaire kern (Rutherford was een mentor van Bohr) en de bovengenoemde spectra van het probleem.

[TOC]

Hoofdkenmerken van het Bohr -model

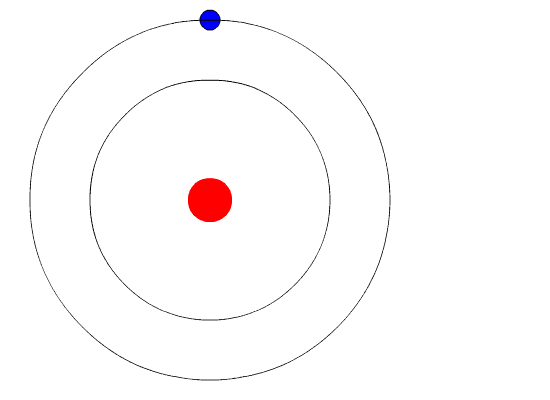Bohr's Atom. De animatie vertegenwoordigt het elektron wanneer het van een hoger niveau van energie naar een andere energie gaat, waardoor een licht van licht (een foton) uitzendt. Bron: Wikimedia Commons.

Het atoommodel van Bohr veronderstelt dat het elektron in een cirkelvormige baan rond de kern beweegt door de werking van de elektrostatische aantrekkingskracht van Coulomb en stelt voor dat het hoekmomentum van het elektron wordt gekwantiseerd.

Kan u van dienst zijn: Balancing Vector: berekening, voorbeelden, oefeningen

Laten we eens kijken hoe beide concepten in wiskundige vorm kunnen worden geïntegreerd:

Laat L de grootte van het hoekmomentum, m de massa van het elektron en de snelheid van het elektron en R de straal van de baan. Om L te berekenen, hebben we:

L = m⋅r⋅V

Bohr stelde voor dat l gelijk was aan hele veelvouden van de constante h/2π, waarbij h de Planck constant, Korte tijd geleden geïntroduceerd door de natuurkundige Max Planck (1858-1947) bij het oplossen van het energieprobleem dat wordt uitgestoten door een zwart lichaam, een theoretisch object dat al het invallende licht absorbeert.

De waarde ervan is h = 6.626 × 10⁻³⁴ J ・ s, terwijl het bij H/2π wordt aangeduid als H, Dat leest  "H Bar".

Daarom blijft de hoekmomentum L:

m⋅r⋅v = nH, Met n = 1,2, 3 ..

En uit deze toestand worden de radio's van de banen toegestaan ​​voor het elektron afgeleid, zoals we dan zullen zien.

Berekening van de elektronen orbit straal

In wat volgt zullen we de eenvoudigste atomen aannemen: waterstof, die bestaat uit een enkel proton en een elektron, zowel met een magnitude -belasting als.

De centripetale kracht die het elektron in zijn cirkelvormige baan houdt, wordt geleverd door elektrostatische aantrekkingskracht, waarvan de grootte F is:

F = ke²/R²

Waarbij k de elektrostatische constante van de Coulomb en R-wet is, de elektronen-eiwitafstand. Wetende dat in een cirkelvormige beweging de centripetale versnelling_C Het wordt gegeven door reden tussen het kwadraat van snelheid en afstand R:

naar_C = V² / R

Volgens de tweede wet van Newton is Net Force het product van Mass M door versnelling:

MV²/r = ke²/R²

Vereenvoudiging van radio R wordt verkregen:

M⋅V²R = ke²

Door deze uitdrukking te combineren met dat van het hoekmomentum hebben we een systeem van vergelijkingen, gegeven door:

Het kan u van dienst zijn: fysiek traject: kenmerken, typen, voorbeelden en oefeningen

1) MV²R = ke²

2) r = n H/MV

Het idee is om het systeem op te lossen en de straal van de toegestane baan te bepalen. Een beetje elementaire algebra leidt tot het antwoord:

R = (nH))² / K⋅M⋅E²

Met n = 1, 2, 3, 4, 5 ..

Voor n = 1 hebben we het minste van de radio's, genoemd Bohr radio a_of Met een waarde van 0,529 × 10⁻¹⁰ M. De radio's van de andere banen worden uitgedrukt in termen van naar_of.

Op deze manier introduceert Bohr het belangrijkste kwantumnummer N, erop wijzend dat de toegestane radio's gebaseerd zijn op de planck -constante, de elektrostatische constante en de massa en belasting van het elektron.

Bohr Atomic Model postuleert

Deense fysicus Niels Bohr (1885-1962).

Bohr combineert vakkundig Newtoniaanse mechanica met de nieuwe ontdekkingen die continu hadden gegeven in de tweede helft van de 19e eeuw en het begin van de 20e eeuw. Onder hen het revolutionaire concept van "hoeveel", waarvan Planck zelf beweerde niet erg overtuigd te zijn.

Door zijn theorie zou Bohr de reeks van het waterstofspectrum naar tevredenheid kunnen verklaren en energieemissies kunnen voorspellen in de rang van de ultraviolet en infrarood, die nog niet was waargenomen.

We kunnen uw postulaten als volgt samenvatten:

Elektronen beschrijven cirkelvormige trajecten

Het elektron draait om de kern in stabiele cirkelvormige baan, met uniforme cirkelvormige beweging. De beweging is te wijten aan de elektrostatische aantrekkingskracht die de kern erop uitoefent.

Het hoekmomentum is gekwantiseerd

Het hoekmomentum van het elektron wordt gekwantiseerd volgens de uitdrukking:

L = mvr = nH

Waarbij n een geheel getal is: n = 1, 2, 3, 4 ..., die leidt tot het elektron kan alleen in bepaalde gedefinieerde banen zijn, waarvan de radio's zijn:

R = (n H))² / k m e²

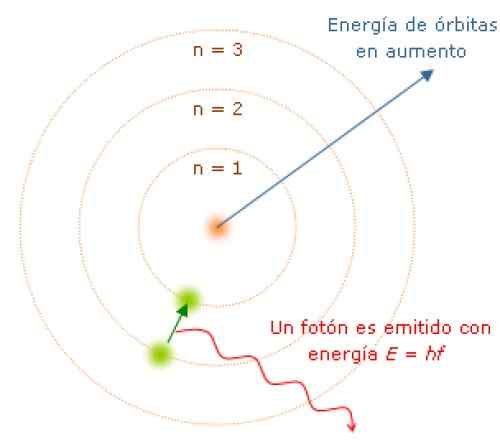
Elektronen die fotonen uitzenden of absorberen wanneer ze van de ene energietoestand naar de andere gaan

Bij het overgaan van de ene energietoestand naar de andere, absorbeert of stoot het elektron in afzonderlijke hoeveelheden die fotonen worden genoemd. Bron: Wikimedia Commons.

Omdat het hoekmomentum wordt gekwantiseerd, energie en ook. Het kan worden aangetoond dat E wordt gegeven door:

Kan u van dienst zijn: verticale opname: formules, vergelijkingen, voorbeelden

En het vervangen van alle constanten wordt een verkorte vorm verkregen:

Het volt -elektron of EV, is een andere eenheid voor energie, veel gebruikt in atomaire fysica. Het negatieve teken in energie zorgt voor de stabiliteit van de baan, wat aangeeft dat werk moet worden verricht om het elektron van deze positie te scheiden.

Terwijl het elektron zich in zijn baan bevindt, absorbeert of stoten geen licht uit. Maar wanneer het van een baan van grotere energie naar een lagere.

De frequentie F van het uitgezonden licht hangt af van het verschil tussen de energieniveaus van de banen:

E = hf = e_voorletter - e_laatste

Beperkingen

Het Bohr -model heeft bepaalde beperkingen:

-Het is alleen met succes van toepassing op het waterstofatoom. Pogingen om het toe te passen op meer complexe atomen werkten niet.

-Het reageert niet waarom sommige banen stabiel zijn en anderen niet. Het feit dat de energie in het atoom werd gekwantiseerd, werkte heel goed, maar het model gaf geen reden, en dat was iets dat ongemak voor wetenschappers veroorzaakte.

-Een andere belangrijke beperking is dat het niet de extra lijnen verklaarde die door atomen zijn uitgegeven in aanwezigheid van elektromagnetische velden (Zeeman -effect en grimmig effect). Of waarom sommige spectrumlijnen intenser waren dan andere.

-Het Bohr -model houdt geen rekening met relativistische effecten, wat nodig is.

-Het neemt vanzelfsprekend aan dat het mogelijk is om precies de positie en snelheid van het elektron te kennen, maar wat echt wordt berekend is de kans dat het elektron een bepaalde positie inneemt.

Ondanks zijn beperkingen had het model destijds groot succes, niet alleen voor het integreren van nieuwe ontdekkingen met reeds bekende elementen, maar omdat het nieuwe vragen toonde, waardoor duidelijk werd dat het pad naar een bevredigende verklaring van het atoom was in de kwantummechanica.

Interessante artikelen

Schrödinger atomair model.

Broglie Atomic Model.

Chadwick Atomic Model.

Heisenberg Atomic Model.

Perrin Atomic Model.

Thomson Atomic Model.

Dalton Atomic Model.

Dirac Jordan Atomic Model.

Democritus Atomic Model.

Leucipo -atoommodel.

Sommend Atomic Model.

Huidig ​​atoommodel.