Minste vierkanten

Wat is de methode van minimale vierkanten?

De methode van Minste vierkanten Het is een van de belangrijkste toepassingen bij de benadering van functies. Het idee is om een ​​curve te vinden zodat, gezien een reeks nette paren, deze functie beter wordt benaderd voor de gegevens. De functie kan een lijn zijn, een kwadratische curve, een kubieke, enz.

Het idee van de methode is om de som van vierkanten van de verschillen in de ordinaten (component Y) te minimaliseren, tussen de punten die worden gegenereerd door de gekozen functie en de punten die tot de gegevensset behoren.

Minimale vierkante methode

Voordat we de methode geven, moeten we eerst duidelijk zijn over wat "het beter is naderen". Stel dat een lijn wordt gevraagd y = b+mx dat is degene die het beste een set n punten vertegenwoordigt, namelijk (x1, y1), (x2, y2) ..., (xn, yn).

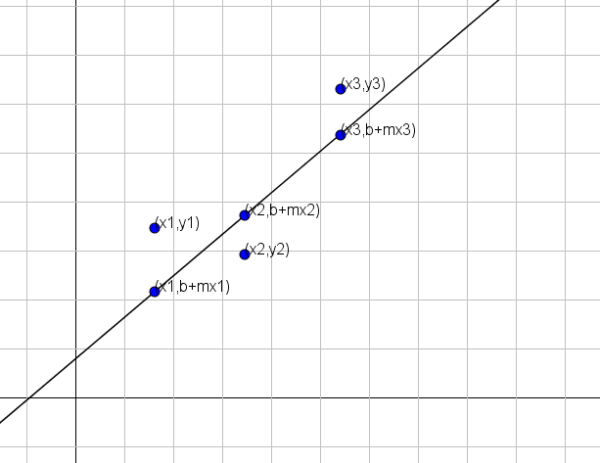
Zoals getoond in de vorige figuur, als de variabelen x en y gerelateerd waren door de lijn y = b+mx, dan zou voor x = x1 de overeenkomstige waarde van y b+mx1 zijn. Deze waarde verschilt echter van de werkelijke waarde van y, wat y = y1 is.

Vergeet niet dat in het vlak de afstand tussen twee punten wordt gegeven door de volgende formule:

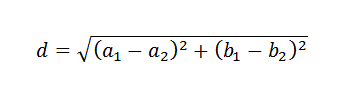
Met dit in gedachten, om te bepalen hoe de lijn Y = B+MX te kiezen die de gegeven gegevens het beste benadert, klinkt het logisch om als criteria te gebruiken de selectie van de lijn die de som van de vierkanten van de afstanden tussen de punten minimaliseert en de lijn.

Aangezien de afstand tussen de punten (x1, y1) en (x1, b+mx1) y1- (b+mx1) is, wordt ons probleem gereduceerd tot het vinden van getallen m en b zodat de volgende som minimaal is:

Kan u van dienst zijn: groene stelling, demonstratie, toepassingen en oefeningen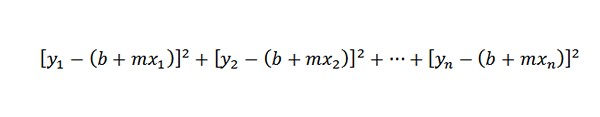

De lijn die aan deze voorwaarde voldoet, staat bekend als de "benadering van de lijn van minimale vierkanten tot de punten (x1, y1), (x2, y2), ..., (xn, yn)".

Zodra het probleem is verkregen, blijft het alleen een methode kiezen om de aanpak te vinden door minimale vierkanten. Als de punten (x1, y1), (x2, y2), ..., (xn, yn) allemaal op de lijn y = mx+b staan, zouden we colineal moeten zijn en:

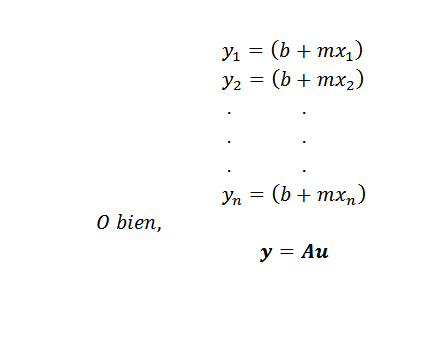
In deze uitdrukking:

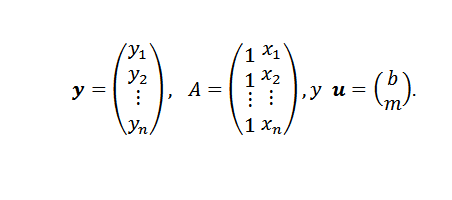
Ten slotte, als de punten niet colineaal zijn, dan kan y-au = 0 en het probleem zich vertalen in het vinden van een vector of zodanig dat de Euclidische standaard minimaal is.

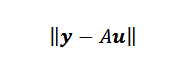
Het vinden van de minimaliserende vector of is niet zo moeilijk als je zou kunnen denken. As is een NX2 en U -matrix is ​​een 2 × 1 -matrix, we hebben dat de Au -vector een vector is in r^N en behoort tot het beeld van A, dat is een subruimte van R^N Met een dimensie niet meer dan twee.

We gaan ervan uit dat n = 3 om te laten zien wat de procedure is die moet worden gevolgd. Als n = 3 is het beeld van A een vlak of een lijn die door de oorsprong gaat.

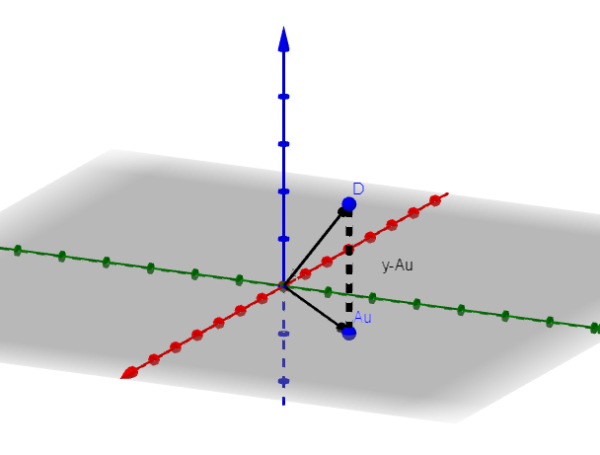
Laat V de minimaliserende vector. In de figuur zien we dat y-au wordt geminimaliseerd wanneer het orthogonaal is voor het beeld van een. Dat wil zeggen, als V de minimaliserende vector is, dan gebeurt het dat:

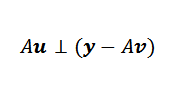
Dan kunnen we het bovenstaande op deze manier uitdrukken:

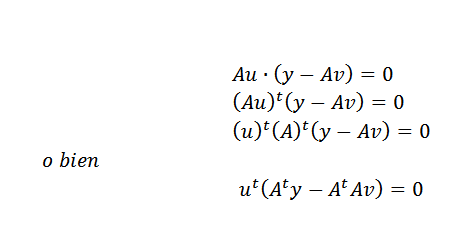
Dit kan alleen gebeuren als:

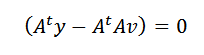
Ten slotte moeten we:

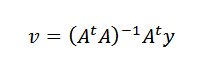
Het is sindsdien mogelijk om dit te doen^TA is omkeerbaar wanneer de n wijst als gegevens niet colineal zijn.

Nu, als we in plaats van naar een lijn te zoeken, we een gelijkenis willen vinden (wiens uitdrukking van de vorm y = a+bx+cx zou zijn²) Dat het een betere benadering van de gegevenspunten was, zou de procedure hieronder worden beschreven.

Kan u van dienst zijn: hele nummers

Als de gegevenspunten in die gelijkenis zouden zijn, zou dit moeten:

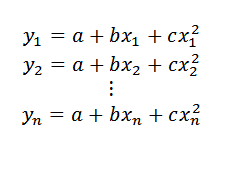
Dan:

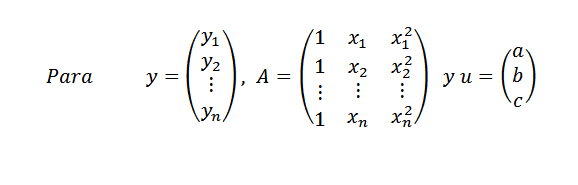
Evenzo kunnen we y = au schrijven. Als alle punten niet in de gelijkenis staan, hebben we dat Y-au anders is van nul voor elke vector U en ons probleem is opnieuw: zoek een vector u in r3 zodat de norm || y-au || zo veel mogelijk zijn.

Door de vorige procedure te herhalen, kunnen we de gewenste vector bereiken is:

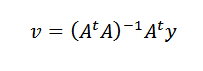
Opgeloste oefeningen

Oefening 1

Zoek de lijn die het beste past bij de punten (1.4), (-2.5), (3, -1) en (4.1).

Oplossing

We moeten:

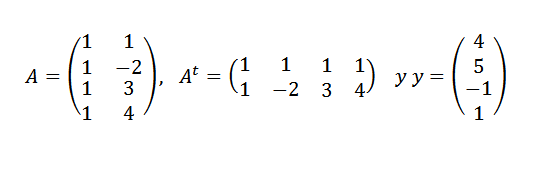
Dan:

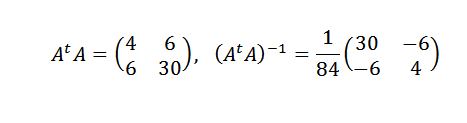
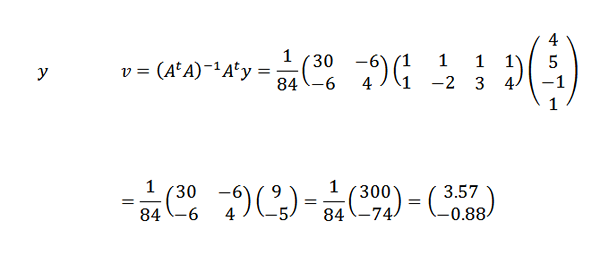
Daarom concluderen we dat de lijn die het beste bij de punten past, wordt gegeven door:

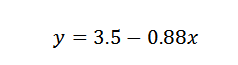
Oefening 2

Stel dat een object wordt gevallen van een hoogte van 200 m. Tijdens het vallen worden de volgende maatregelen genomen:

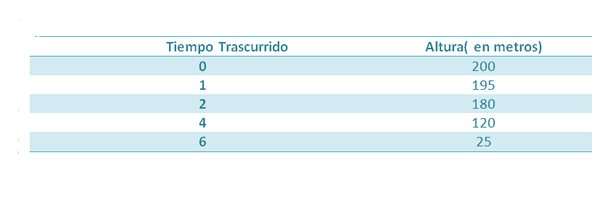
We weten dat de hoogte van dit object, na een tijd is verstreken, wordt gegeven door:

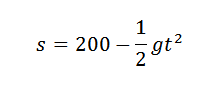
Als we de waarde van G willen verkrijgen, kunnen we zoeken naar een gelijkenis die een betere benadering is van de vijf punten die in de tabel worden gegeven, en dus zouden we de coëfficiënt hebben die vergezelt² Het zal een redelijke benadering zijn van (-1/2) G als de metingen exact zijn.

We moeten:

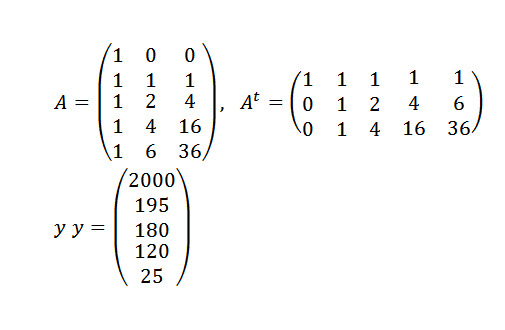
En dan:

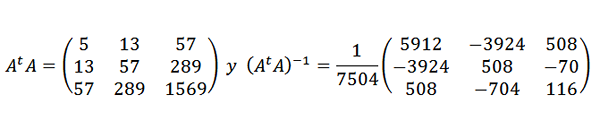
Dus de gegevenspunten worden aangepast door de volgende kwadratische expressie:

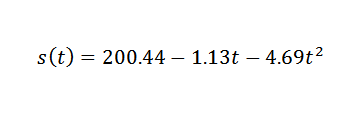
Dus je moet:

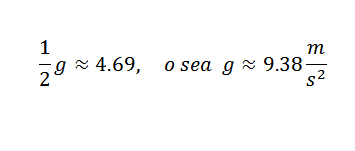
Dit is een waarde die redelijk dicht bij de juiste ligt, wat g = 9,81 m/s is². Om een ​​meer accurate G van G te verkrijgen, zou het nodig zijn om te beginnen met meer precieze observaties.

Waar is de minimale vierkante methode voor?

In de problemen die zich voordoen in natuurlijke of sociale wetenschappen is het handig om de relaties tussen verschillende variabelen te schrijven door een wiskundige uitdrukking.

Kan u van dienst zijn: proportionele variatie

We kunnen bijvoorbeeld in economie de kosten (c), inkomsten (i) en winst (u) verhouden via een eenvoudige formule:

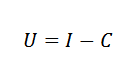
In de natuurkunde kunnen we de versnelling veroorzaken die wordt veroorzaakt door de zwaartekracht, de tijd waarin een object is gevallen en de hoogte van het object bij wet:

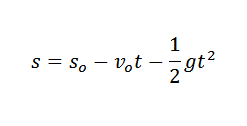
In de vorige uitdrukking s_of Het is de eerste hoogte van het object en v_of Is uw initiële snelheid.

Het vinden van dergelijke formules is echter geen eenvoudige taak; Het komt meestal overeen met de professional die dienst heeft om met veel gegevens te werken en herhaaldelijk verschillende experimenten uit te voeren (om te controleren of de verkregen resultaten constant zijn) om relaties tussen de verschillende gegevens te vinden.

Een gebruikelijke manier om dit te bereiken is om de gegevens die in een vlak zijn verkregen als punten weer te geven en een continue functie te zoeken die deze punten optimaal benadert.

Een van de manieren om de functie te vinden die de gegeven gegevens "beter benadert", is volgens de methode van de vierkante minima.

Bovendien, zoals we ook in de oefening zagen, kunnen we dankzij deze methode vrij nauwe benaderingen voor fysieke constanten bereiken.