Geschatte meting van amorfe cijfers Voorbeeld en lichaamsbeweging

De Benaderen Van de amorfe figuren bestaat uit een reeks methoden die worden gebruikt om het gebied of perimeter van geometrische figuren te bepalen die geen driehoeken, vierkanten, cirkels, enz. Zijn. Sommige kunnen worden uitgebreid naar drie -dimensionale cijfers.

In principe bestaat de meting uit regelmatig reticuleren, zoals rechthoeken, vierkanten of trapezoïden, die ongeveer het oppervlak bedekken. De nauwkeurigheid van de benadering van het gebied verkregen door deze methoden neemt toe met de finesse of dichtheid van het reticulate.

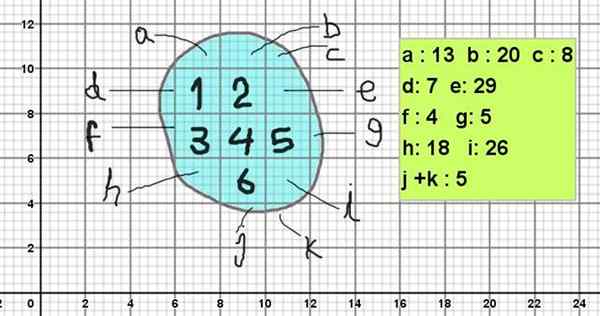
Figuur 1. Stenen in de vorm van amorfe figuren. Bron: PxFuel.

Figuren 1 en 2 tonen verschillende amorfe figuren. Om het gebied te berekenen, een reticulaire, samengesteld uit 2 x 2 vierkanten, die op hun beurt zijn onderverdeeld in twintig -vijf vierkanten van 2/5 x 2/5.

Het toevoegen van de gebieden van de hoofdvierkanten en de secundaire vierkanten wordt het geschatte gebied van de amorfe figuur verkregen.

Figuur 2. Een reticulair om het gebied van een van de amorfe figuren op een geschatte manier te berekenen. Bron: f. Zapata

[TOC]

Gebied onder een curve

Het is vaak nodig om het gebied te berekenen onder een curve tussen twee limietwaarden. In dit geval kunnen rechthoekige strepen in plaats van een vierkant reticulair worden getraceerd over het gebied onder de genoemde curve.

De som van alle rechthoekige strepen wordt genoemd Riemann's som of som. Figuur 3 toont een partitie van het interval [a, b] waarop u ongeveer het gebied onder de curve wilt bepalen.

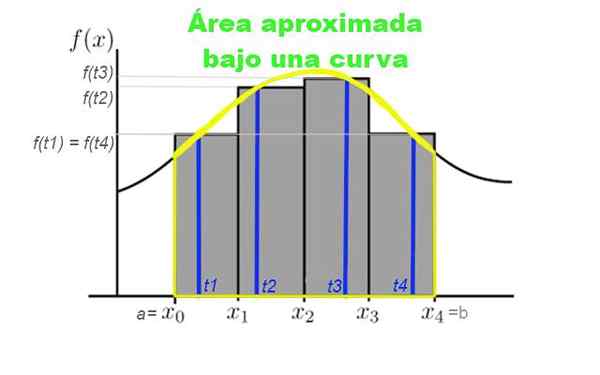figuur 3. Partitie van het interval [A, B] in vier subintervallen, die meestal uit dezelfde breedte zijn genomen. De hoogte van de rechthoeken wordt bepaald door de waarde van de curve voor een TK die tot de subintervallen hoort. Bron: f. Zapata.

Stel dat u het gebied wilt berekenen onder de curve gegeven door de functie y = f (x), waarbij x behoort tot het interval [a, b] waarbinnen u het gebied wilt berekenen. Hiervoor wordt een verdeling van N -elementen binnen dit interval gemaakt:

Kan u van dienst zijn: 60 delers

Partition = x0 = a, x1, x2, ..., xn = b.

Vervolgens wordt het geschatte gebied onder de curve gegeven door y = f (x) in het interval [a, b] bereikt door de volgende som:

S = ∑_{K = 1}^N F (T_k) (X_k - X_K-1))

Waar T_k is tussen x_K-1 en x_k: X_K-1 ≤ t_k ≤ x_k .

Figuur 3 toont de som van riemann van de curve y = f (x) in het interval [x0, x4]. In dit geval werd een partitie van vier subintervallen gemaakt en de som vertegenwoordigt het totale oppervlakte van de grijze rechthoeken. 

Deze som vertegenwoordigt een benadering van het gebied onder de curve f tussen de abscissas x = x0 en x = x4.

De benadering van het gebied onder de curve verbetert in de mate dat het nummer N van partities is groter en is meestal precies het gebied onder de curve wanneer het nummer N partities neigt naar oneindig. 

In het geval dat de curve wordt weergegeven door een analytische functie, de waarden f (t_k) Ze worden berekend om de genoemde functie in de waarden T te evalueren_k. Maar als de curve geen analytische uitdrukking heeft, blijven de volgende mogelijkheden bestaan:

1. Benader de curve door een functie, bijvoorbeeld een polynoom.
2. Neem de Cartesiaanse coördinaten van de punten waar de curve wordt onderschept met de lijnen x = t_k.

Regelmatige intervallen

Afhankelijk van de keuze van de TK -waarde in het interval [x_k, X_K-1], de som kan de exacte waarde van het gebied van het gebied onder de curve van de functie y = f (x) overschatten of onderschatten. Het meest raadzame is om het TK -punt te nemen waar het ontbrekende gebied ongeveer gelijk is aan het resterende gebied, hoewel het niet altijd mogelijk is om een ​​dergelijke keuze te maken.  

Kan u van dienst zijn: multiplicatief inverse: uitleg, voorbeelden, opgeloste oefeningen

Neem Tk aan het einde

Het meest praktische is dan om regelmatige intervallen van brede Δx = (b - a)/n te gebruiken, waarbij a en b de minimale en maximale waarden van de abscis zijn, terwijl n het aantal onderverdelingen is.

In dat geval nadert het gebied onder de curve door:

Gebied = f (a+Δx)+f (a+2Δx)+…+f [a+(n-1] Δx+f (b)*Δx

In de vorige uitdrukking werd Tk aan de rechterkant van de subinterval genomen.

Neem TK aan de linkerkant

Een andere praktische mogelijkheid is om de TK -waarde aan de linkerkant te nemen, in welk geval de som die het gebied benadert, wordt uitgedrukt als:

Gebied = [f (a)+f (a+Δx)+…+f (a+(n-1) Δx)*Δx

TK als centrale waarde

In het geval dat Tk wordt gekozen als de centrale waarde van de reguliere subinterval van Ax -breedte, is de som die het gebied onder de curve benadert:

Gebied = [f (a+Δx/2)+f (a+3Δx/2)+…+f (b- Δx/2)]*Δx

Elk van deze uitdrukkingen heeft de neiging om de exacte waarde te hebben voor zover het aantal onderverdelingen willekeurig groot is, dat wil zeggen dat Δx de neiging heeft op nul, maar in dit geval is het aantal voorwaarden van de som enorm groot met de daaruit voortvloeiende rekenkosten. 

Voorbeeld

Figuur 2 toont een amorfe figuur, waarvan de contour vergelijkbaar is met de stenen van afbeelding 1. Om het gebied te berekenen, wordt het op een reticulate geplaatst met hoofdvierkanten van 2 x 2 eenheden voor het vierkant (ze kunnen bijvoorbeeld 2 cm² zijn).

En omdat elk vierkant wordt onderverdeeld in 5 x 5 onderverdelingen, heeft elke onderverdeling een oppervlakte van 0,4 x 0,4 vierkante eenheden (0,16 cm²).

De figuur in de figuur zou als volgt worden berekend:

Kan u van dienst zijn: gemeenschappelijke factorisatie: voorbeelden en oefeningen

Gebied = 6 x 2 cm² + (13 + 20 + 8 + 7 + 29 + 4 + 5 + 18 + 26 + 5) x 0,16 cm²

Het is te zeggen:

Gebied = 12 cm² + 135 x 0,16 cm² = 33,6 cm².

Oefening opgelost

Bereken ongeveer het gebied onder de curve gegeven door de functie f (x) = x² Weddenschap a = -2 tot b = +2. Schrijf hiervoor de som voor n reguliere partities van het interval [a, b] en neem vervolgens de wiskundige limiet voor het geval dat het aantal partities de neiging heeft om oneindig te zijn. 

Oplossing

Ten eerste wordt het partitie -interval gedefinieerd als 

Δx = (b - a)/n. 

Dan is de som voor het recht dat overeenkomt met de functie f (x) als volgt:

A = -2 en b =+2 worden vervangen zodat het interval of de stap Δx = 4/n is. In dit geval de som voor de functie f (x) = x² is:

 Het vierkante binomiale is ontwikkeld: 

[-2 +(4i/n)]² = 4 - 16 i /n + (4 /n)² Je²

En dan wordt het in de som vervangen:

Het scheiden van de samenvatting en het nemen van de constante hoeveelheden als een gemeenschappelijke factor van elke som wordt verkregen:

 De eerste van de som, de tweede is:

En de derde is:

Vervangen in de uitdrukking van de som die je hebt:

S (f, n) = 16 - 64 (n+1)/2n+64 (n+1) (2n+1)/6n²

Bij het kiezen van een grote waarde voor N heb je een goede benadering van het gebied onder de curve. In dit geval is het echter mogelijk om de exacte waarde te bereiken die de wiskundige limiet neemt wanneer N de neiging heeft oneindig te zijn:

Gebied = lim_{N-> ∞}[16 - 64 (n+1)/2n+64 (n+1) (2n+1)/6n²]

Gebied = 16 - (64/2)+ (64/3) = 16/3 = 5.333.

Referenties

1. Casteleiro, J. M. 2002. Uitgebreide berekening (geïllustreerde editie). Madrid: ESIC -redactie.
2. Larson, r. 2010. Berekening van een variabele. 9NA. Editie. McGraw Hill.
3. Purcell, E. 2007. Berekening met analytische geometrie. 9NA. Editie. Pearson Education.
4. Unicaans. Geschiedenis van het concept van integrale. Hersteld van: repository.Unicaans.is
5. UIS. Riemann Sums. Hersteld van: wiskunde.UIS.Edu.co
6. Wikipedia. Gebied. Hersteld van: is.Wikipedia.com