Discrete wiskunde

Wat zijn discrete wiskunde?

De discrete wiskunde komen overeen met een wiskundegebied dat verantwoordelijk is voor het bestuderen van de reeks natuurlijke getallen; dat wil zeggen, de set eindige en oneindige boekhoudnummers waar de elementen afzonderlijk kunnen worden geteld, één voor één.

Deze sets staan ​​bekend als discrete sets; Een voorbeeld van deze sets zijn hele getallen, grafieken of logische uitdrukkingen, en worden toegepast op verschillende gebieden van de wetenschap, voornamelijk in informatica of computergebruik.

Beschrijving

In discrete wiskunde zijn de processen te kweken, ze zijn gebaseerd op de volledige nummers. Dit betekent dat decimale getallen niet worden gebruikt en daarom wordt de benadering of limieten, zoals in andere gebieden, ook niet gebruikt. Een onbekende kan bijvoorbeeld gelijk zijn aan 5 of 6, maar nooit 4,99 of 5.9.

Aan de andere kant zullen de variabelen in de grafische weergave discreet zijn en worden ze gegeven vanuit een eindige set punten, die één voor één worden geteld, zoals waargenomen in de afbeelding:

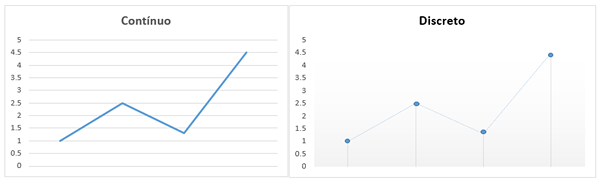
Discrete wiskunde is geboren vanwege de noodzaak om een ​​exacte studie te verkrijgen die kan worden gecombineerd en bewezen, om dit op verschillende gebieden toe te passen.

Wat zijn discrete wiskunde voor?

Discrete wiskunde wordt op meerdere gebieden gebruikt. Onder de belangrijkste zijn de volgende:

Combinatorisch

Studie eindige sets waar de elementen kunnen worden besteld of gecombineerd en teruggeroepen.

Discrete distributietheorie

Studie -gebeurtenissen die plaatsvinden in ruimtes waar monsters boekhouding kunnen zijn, waarbij continue distributies worden gebruikt om discrete distributies te benaderen, of tegengesteld.

Informatietheorie

Het verwijst naar het coderen van informatie, gebruikt voor het ontwerp en de overdracht en opslag van gegevens, zoals vergelijkbare signalen.

Kan u van dienst zijn: Trachtenberg -methode: wat is het, voorbeelden

Reken-

Door discrete wiskunde worden problemen opgelost met behulp van algoritmen, evenals wat kan worden berekend en de tijd die nodig is om het te doen (complexiteit).

Het belang van discrete wiskunde op dit gebied is de afgelopen decennia toegenomen, vooral voor de ontwikkeling van programmeren en Software.

Cryptografie

Het is gebaseerd op discrete wiskunde om veiligheidsstructuren of coderingsmethoden te creëren. Een voorbeeld van deze applicatie zijn wachtwoorden, het verzenden van afzonderlijke bits die informatie bevatten.

Door de studie kunnen de eigenschappen van hele getallen en priemgetallen (theorie van getallen) worden gemaakt of vernietigd.

Logica

Discrete structuren worden gebruikt, die meestal een eindige set vormen, om stellingen aan te tonen of bijvoorbeeld software te verifiëren.

Graph -theorie

Het maakt de oplossing van logische problemen mogelijk, met behulp van knooppunten en lijnen die een type grafiek vormen, zoals weergegeven in de volgende afbeelding:

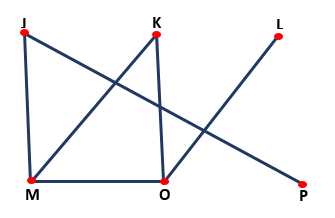Algebra

Het is een gebied dat nauw verbonden is met discrete wiskunde omdat algebraïsche uitdrukkingen discreet zijn. Via deze elektronische circuits worden verwerkers, programmering (Boolean Algebra) en databases (relationele algebra) ontwikkeld (relationele algebra).

Geometrie

Bestudeer de combinatorische eigenschappen van geometrische objecten, zoals vlakke coating. Aan de andere kant maakt computationele geometrie het mogelijk om geometrische problemen te ontwikkelen door algoritmen toe te passen.

Set Theory

In discrete wiskunde zijn de sets (eindig en oneindig gevoelloos) het belangrijkste doelstelling. De ingestelde theorie werd gepubliceerd door George Cantor, die aantoonde dat alle oneindige sets dezelfde grootte hebben.

Een set is een groep elementen (cijfers, dingen, dieren en mensen, onder andere) die goed zijn gedefinieerd; dat wil zeggen, er is een relatie volgens welke elk element tot een set behoort en wordt bijvoorbeeld een ∈ A uitgedrukt.

Kan u van dienst zijn: eigenschappen van gelijkheid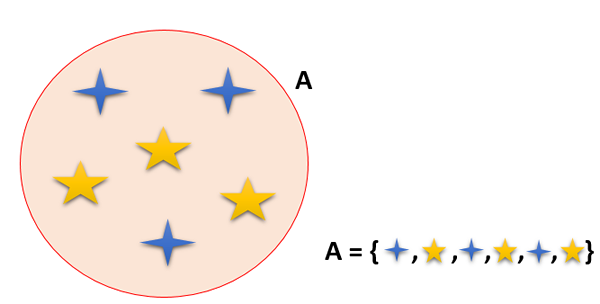

In de wiskunde zijn er verschillende sets die bepaalde cijfers groeperen volgens hun kenmerken. Zo hebben ze bijvoorbeeld:

- Set van natuurlijke getallen n = 0, 1, 2, 3, 4, 5, 6, ... +∞.

- Set van hele getallen e = -∞…, -3, -2, -1, 0, 1, 2, 3,… +∞.

- Subset van rationele getallen q* = -∞…, - ¼, - ½, 0, ¼, ½,… ∞.

- Set reële getallen r = -∞…, -½, -1, 0, ½, 1,… ∞.

De sets worden genoemd met alfabetbrieven, in hoofdletters; Terwijl de elementen in kleine letters worden genoemd, in de sleutels () en gescheiden door komma's (,). Ze zijn over het algemeen weergegeven in diagrammen zoals Venn en Caroll, evenals computationeel.

Met basisoperaties zoals Union, kruising, complement, verschil en Cartesiaans product, worden de sets en hun elementen beheerd, op basis van de beledingsrelatie.

Er zijn verschillende soorten sets, de meest bestudeerde in discrete wiskunde zijn de volgende:

Eindige set

Het is er een met een eindig aantal elementen en dat komt overeen met een natuurlijk aantal. Dus bijvoorbeeld, a = 1, 2, 3,4 is een eindige set met 4 elementen.

Oneindige boekhoudset

Het is er een waarin er een correspondentie is tussen de elementen van een set en de natuurlijke getallen; dat wil zeggen, vanuit een element kunnen alle elementen van een set achtereenvolgens worden vermeld.

Op deze manier komt elk element overeen met elk element van de set natuurlijke getallen. Bijvoorbeeld:

De gehele gehele getallen z = … -2, -1, 0, 1, 2 ... kan worden vermeld als z = 0, 1, -1, 2, -2 .... Op deze manier is het mogelijk om een ​​één -tot -één correspondentie te maken tussen de elementen van Z en de natuurlijke getallen, zoals te zien is in de volgende afbeelding:

Kan u van dienst zijn: berekening van benaderingen met behulp van differentiëlen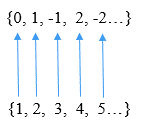

Discretisering

Het is een methode die wordt gebruikt om continue problemen (modellen en vergelijkingen) op te lossen die moeten worden omgezet in afzonderlijke problemen, waarbij de oplossing bekend is met de benadering van de oplossing van het continue probleem.

Anders gezien probeert de discretisatie een eindig bedrag van een oneindige reeks punten te krijgen; Op deze manier wordt een continue eenheid omgezet in individuele eenheden.

Over het algemeen wordt deze methode gebruikt in de numerieke analyse, zoals in de oplossing van een differentiaalvergelijking, via een functie die wordt weergegeven door een eindige hoeveelheid gegevens in het domein, zelfs wanneer dit continu is.

Een ander voorbeeld van de discretisatie is het gebruik ervan om een ​​analoog naar digitaal signaal te converteren, wanneer continue signaaleenheden worden omgezet in individuele eenheden (ze zijn discretiseerd) en vervolgens gecodeerd en gekwantificeerd om digitaal signaal te verkrijgen.

Referenties

1. Grimaldi, r. P. (1997). Discrete en combinatorische wiskunde. Redactionele addison Wesley IberoAmericana.
2. Ferrando, V. Gregori. (negentienvijfennegentig). Discrete wiskunde. Galm.
3. Jech, T. (2011). Set Theory. Stanford Encyclopedia of Philosophy.
4. José Francisco Villalpando Becerra, een. G. (2014). Discrete wiskunde: applicaties en oefeningen. Patria -redactiegroep.
5. Landau, r. (2005). Berekenen, tot eerste cursus wetenschappelijk.
6. Merayo, f. G. (2005). Discrete wiskunde. Thomson redactioneel.
7. Rosen, K. H. (2003). Discrete wiskunde en zijn toepassingen. McGraw-Hill redactioneel.
8. Schneider, D. G. (negentienvijfennegentig). Een logische benadering van discrete wiskunde.