Blokken algebra -elementen, voorbeelden, oefeningen opgelost

Hij Blok algebra Het verwijst naar de reeks bewerkingen die via blokken worden uitgevoerd. Deze en sommige meer elementen dienen om schematisch een systeem te vertegenwoordigen en uw reactie op een specifieke invoer eenvoudig te visualiseren.

Over het algemeen bevat een systeem verschillende elektrische, elektronische en elektromechanische elementen, en elk van hen, met hun respectieve functie en positie in het systeem, evenals de manier waarop ze gerelateerd zijn, is gechematiseerd door functionele blokken.

Figuur 1.

In de bovenstaande figuur is er een zeer eenvoudig systeem, dat bestaat uit een ingangssignaal X (s), dat het blok binnenkomt met de overdrachtsfunctie G (s) die het wijzigt en de uitgang Y (s) produceert.

Het is handig om de signalen en hun reis door het systeem te vertegenwoordigen door pijlen die binnenkomen en elk blok verlaten. Meestal wordt de signaalstroom van links naar rechts gericht.

Het voordeel van dit soort schema's is de visuele hulp die het biedt om het systeem te begrijpen, hoewel het geen fysieke weergave van hetzelfde vormt. In feite is het blokdiagram niet uniek, omdat volgens het standpunt zelfs verschillende diagrammen van hetzelfde systeem kunnen worden getrokken.

Het kan ook gebeuren dat hetzelfde diagram wordt gebruikt voor verschillende systemen die niet noodzakelijkerwijs gerelateerd zijn aan elkaar, op voorwaarde dat het gedrag goed beschrijft. Er zijn verschillende systemen waarvan de reactie in veel aspecten vergelijkbaar is, bijvoorbeeld een LC-circuit (inductor-kanaal) en een massa-resortsysteem.

[TOC]

Wat is een blokdiagram?

De systemen zijn meestal ingewikkelder dan die van figuur 1, maar de blokalgebra biedt een reeks eenvoudige regels om het systeemschema te manipuleren en te verminderen tot de eenvoudigste versie.

Zoals in het begin wordt uitgelegd, gebruikt het diagram blokken, pijlen en cirkels om de relatie tussen elke systeemcomponent en de stroom van de signalen die erdoorheen lopen te vestigen.

Blockalgebra maakt het mogelijk om twee of meer signalen te vergelijken door som, aftrekking en vermenigvuldiging ervan, en de bijdrage te analyseren die elke component aan het systeem levert.

Dankzij dit is het mogelijk om het hele systeem te verminderen tot een enkel ingangssignaal, een unieke overdrachtsfunctie die de systeemactie en de bijbehorende uitgang volledig beschrijft.

Het kan u dienen: Astroclypics: geschiedenis, welke studies, takken

Blokdiagramelementen

De elementen van het blokdiagram zijn de volgende:

Het signaal

De signalen zijn zeer gevarieerd, het is bijvoorbeeld gebruikelijk dat het een elektrische stroom of een spanning is, maar het kan helder, geluid en meer zijn. Het belangrijkste is dat het informatie bevat over een bepaald systeem.

Het signaal wordt aangeduid met een hoofdletter als het een functie van de variabele is S van de Laplace -transformatie: x (s) (zie figuur 1) of met kleine letters als deze op de tijd is gebaseerd T, Als x (t).

In het blokdiagram wordt het ingangssignaal weergegeven door een pijl die naar het blok is gericht, terwijl het uitgangssignaal, aangeduid als y (s) of (t), wordt aangegeven met een uitgaande pijl.

Zowel het invoer- als het uitgangssignaal zijn uniek en het adres waarin de informatie stroomt wordt bepaald door de richting van de pijl. En algebra is hetzelfde voor een van de twee variabelen.

Het blok

Het blok wordt weergegeven door een vierkant of een rechthoek (zie figuur 1) en kan worden gebruikt om bewerkingen uit te voeren of de overdrachtsfunctie te implementeren, die meestal wordt aangegeven met de hoofdletter G. Deze functie is een wiskundig model waarmee de door het systeem aangeboden reactie wordt beschreven vóór een instapsignaal.

De overdrachtsfunctie kan in termen van tijd worden uitgedrukt T zoals g (t) of de variabele S zoals g (s).

Wanneer het ingangssignaal X (s) naar het blok aankomt, wordt het vermenigvuldigd met de overdrachtsfunctie en wordt het getransformeerd in het uitgangssignaal y (s). Wiskundig wordt het als volgt uitgedrukt:

En (s) = x (s).G (s)

Evenzo is de overdrachtsfunctie de verhouding tussen de Laplace -transformatie van het uitgangssignaal en de Laplace -transformatie van het ingangssignaal, op voorwaarde dat de beginvoorwaarden van het systeem nul zijn:

G (s) = y (s) / x (s)

Sompunt

De som of zomer wordt gesymboliseerd door een cirkel met een kruis binnenin. Het wordt gebruikt om, door bedragen en aftrekking, twee of meer signalen te combineren. Aan het einde van de pijl die het signaal symboliseert, wordt een teken + direct geplaatst als dat signaal wordt toegevoegd of een teken - indien afgetrokken.

In de volgende figuur is er een voorbeeld van hoe de zomer werkt: u hebt het ingangssignaal X, waaraan signalen A en B worden toegevoegd, waardoor de exit wordt verkregen en, die algebraïsch is gelijk aan:

Kan u van dienst zijn: verticale opname: formules, vergelijkingen, voorbeelden

Y = x+a+b

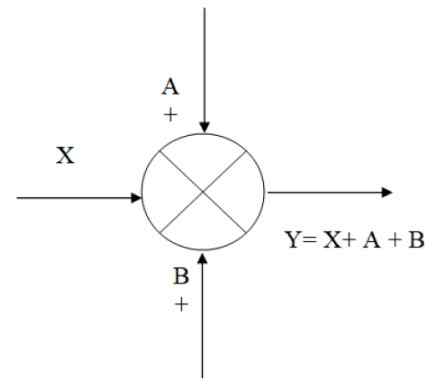Figuur 2. Voorbeeld van een handhaving. Bron: f. Zapata.

Vertakkingspunt

Het wordt ook genoemd Bifurcatiepunt. Daarin wordt het signaal dat uit een blok komt verdeeld over andere blokken of naar een pluim. Het wordt weergegeven door een punt dat op de pijl van het signaal wordt geplaatst en er komt een andere pijl uit die het signaal omleidt naar een ander deel.

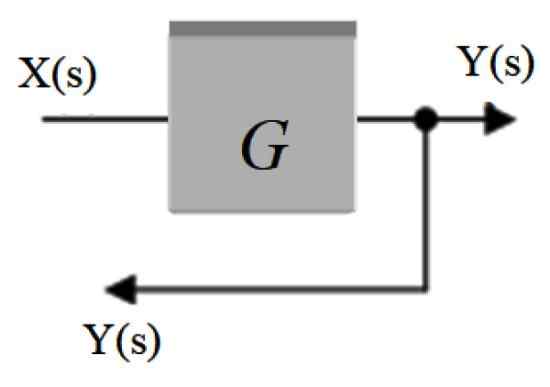figuur 3. Vertakkingspunt. Bron: f. Zapata.

Voorbeelden van blokken van de blokalgebra

Zoals eerder uitgelegd, is het idee om het systeem uit te drukken via het blokdiagram en het te verminderen om de overdrachtsfunctie te vinden die het beschrijft. Hierna volgen de regels van de blokalgebra om de diagrammen te vereenvoudigen:

Cascade -blokken

Wanneer u een signaal heeft dat achtereenvolgens door de G -blokken gaat₁, G₂, G₃..., het wordt gereduceerd tot een uniek blok waarvan de overdrachtsfunctie het product is van G₁, G₂, G₃..

In het volgende voorbeeld voert signaal X (s) het eerste blok in en de uitgang ervan is:

EN₁(s) = x (s).G₁(S)

Figuur 4. Twee blokken in waterval. Bron: f. Zapata.

Op zijn beurt en₁(s) Voer het G -blok in₂(s), wiens vertrek is:

EN₂(s) = x (s).G₁(S). G₂(S)

De procedure is geldig voor N Cascade -blokken:

EN_N (s) = x (s). G₁(S).G₂(S) ... g_N(S)

Blokken parallel

In het linker diagram is het X (S) -signaal Bifurca om de G -blokken in te voeren₁(S) en g₂(S):

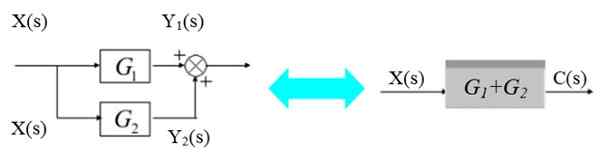Figuur 5. Twee blokken parallel. Bron: f. Zapata.

De respectieve uitgangssignalen zijn:

EN₁(s) = x (s).G₁(S)

EN₂(s) = x (s).G₂(S)

Deze signalen worden toegevoegd om te verkrijgen:

C (s) = y₁(s) +₂(s) = x (s).[G₁(s) + g₂(S)]

Zoals weergegeven in het juiste diagram.

Verplaats een vrijer naar links

Een zomer kan als volgt links van het blok bewegen:

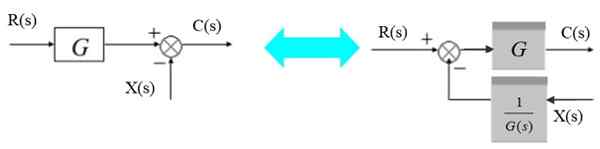Figuur 6. Verplaats de addor links van het blok. Bron: f. Zapata.

Links is het uitgangssignaal:

C (s) = r (s). G (s) - x (s)

Gelijk aan rechts:

C (s) = [r (s) - x (s)/g (s)]].G (s)

Verplaats een recht naar rechts

De zomer kan als volgt rechts van het blok gaan:

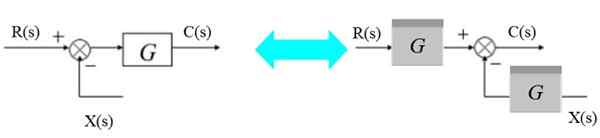Figuur 7. Verplaats een plot rechts van het blok. Bron: f. Zapata.

Links heb je: [r (s) - x (s)].G (s) = c (s)

Kan u van dienst zijn: Archimedes Principe: formule, demonstratie, toepassingen

En aan de rechterkant:

R (s). G (s) - x (s).G (s) = c (s)

Verplaats een bifurcatiepunt van links naar rechts

Om het bifurcatiepunt van links naar rechts van het blok te verplaatsen, is het voldoende om op te merken dat de uitgang C (s) naar rechts product x (s) is.G (s). Omdat je weer X (S) wilt worden, wordt het vermenigvuldigd met het omgekeerde van G (S).

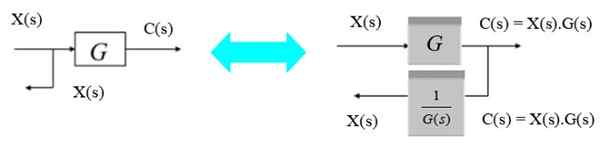Figuur 8. Verplaats een filiaalpunt van links naar rechts. Bron: f. Zapata.

Verplaats een bifurcatiepunt van rechts naar links

Als alternatief kan het bifurcatiepunt als volgt van rechts naar links gaan:

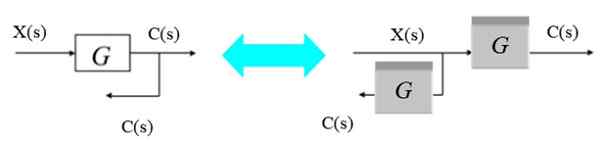Figuur 9. Verplaats een filiaalpunt van rechts naar links. Bron: f. Zapata.

Omdat de uitvoer van de bifurcatie C (s) wil verkrijgen, wordt een nieuw blok G (s) eenvoudig afgewisseld op een bifurcatiepunt aan de linkerkant van het oorspronkelijke blok.

Systeem met feedback

In het volgende systeem wordt het uitgangssignaal C (s) voeders door de onderdanige aan de linkerkant:

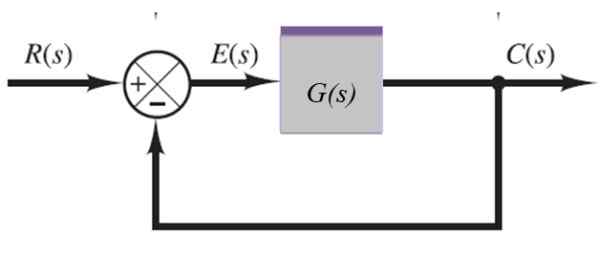Figuur 10. Systeem met feedback. Bron: f. Zapata.

C (s) = e (s).G (s)

Maar:

E (s) = r (s) -c (s)

Het vervangen van deze uitdrukking in de vorige vergelijking is: c (s) = [r (s) -c (s)]].G (s), waaruit C (s) kan worden gewist:

C (s) + c (s).G (s) = r (s).G (s) → C (s). [1 + g (s)] = r (s).G (s)

C (s) = r (s).G (s) / [1 + g (s)]

Of anders:

C (s) / r (s) = g (s) / [1 + g (s)]]

Grafisch, na vereenvoudiging is het:

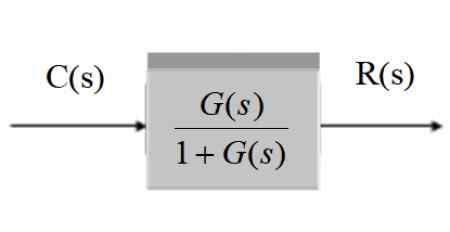Figuur 11. Vereenvoudiging van een systeem met feedback. Bron: f. Zapata.

Systeem met feedback en transducer

De transducer bestaat uit de overdrachtsfunctie h (s):

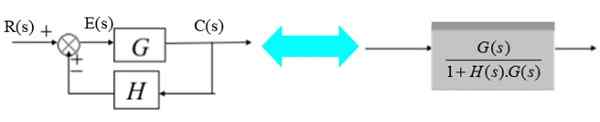Figuur 12. Systeem met feedback en transducer. Bron: f. Zapata.

In het juiste diagram is het uitgangssignaal C (s):

C (s) = e (s). G (s) met e (s) = r (s) - c (s).H (s)

Dus:

C (s) = [r (s) - c (s). H (s)]. G (s)

C (s) [1+ H (s).G (s)] = r (s).G (s)

Daarom kunnen C (s) worden opgeruimd door:

C (s) = g (s).R (s) / [1+ H (s).G (s)]

En de overdrachtsfunctie zal zijn:

G (s) / [1+ H (s).G (s)]

Zoals weergegeven in het vereenvoudigde rechter diagram.

Opgeloste oefeningen

Oefening 1

Zoek de overdrachtsfunctie van het volgende systeem:

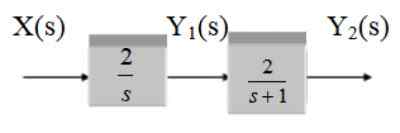Figuur 13. Twee bloksysteem in waterval. Bron: f. Zapata.

Oplossing

Het zijn twee cascadeblokken, daarom is de overdrachtsfunctie het product van de functies G₁ en g₂.

Je moet:

G₁ = 2/s

G₂ = 2 /(S+1)

Daarom is de gezochte overdrachtsfunctie:

G (s) = 4 / [s (s+1)]

Oefening 2

Verminder het volgende systeem:

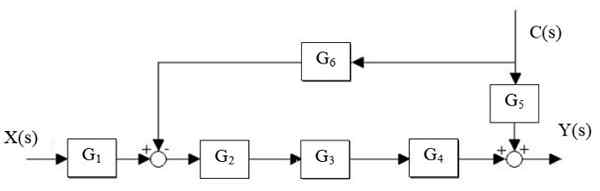Figuur 14. Vereenvoudiging van een systeem. Bron: f. Zapata.

Oplossing

Eerst wordt de G -cascade verminderd₂, G₃ en g_4, En de parallelle G is gescheiden₅ en g₆:

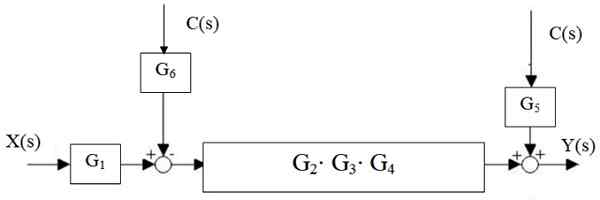Figuur 15. Centrale watervalreductie. Bron: f. Zapata.

Vervolgens de aanbidder links van het G -blok₂ ⋅g₃ ⋅ g₄ Hij gaat naar rechts:

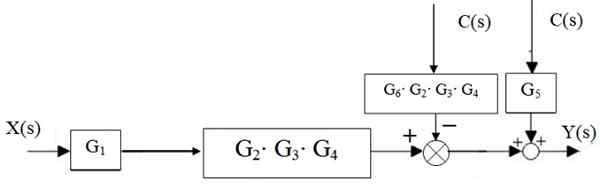Figuur 16. Overdracht van de adminator. Bron: f. Zapata.

De zomers van rechts worden gereduceerd tot één, evenals de cascadeblokken:

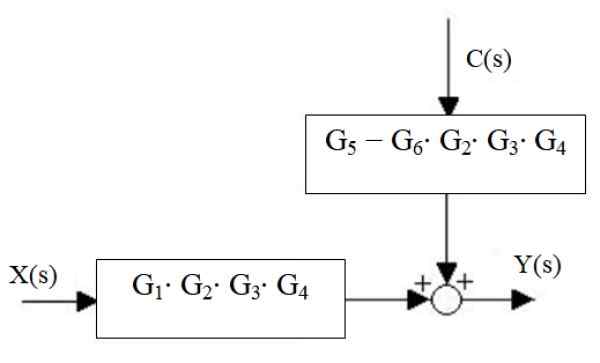Figuur 17. Vermindering van de nieuwe waterval en de zomers van rechts. Bron: f. Zapata.

Ten slotte is de systeemuitgang:

En (s) = x (s) ⋅G₁⋅ g₂ ⋅g₃ ⋅ g₄ + C (s) ⋅ [g₅ - G₆ ⋅ g₂ ⋅g₃ ⋅ g₄]

Referenties

1. Alaydi, J. Systeemblokdiagramregeling. Hersteld van: site.Iugaza.Edu.$.
2. Bolton, W. 2006. Regeltechniek. 2e. Editie. Alfa omega.
3. Cwalinsky, J. Inleiding tot System Block Algebra. Hersteld van: cedengineering.com.
4. DademuchConnection. Blokken diagram. Hersteld van: Dademuch.com.
5. Ogata, K. 2010. Modern Control Engineering. 5e. Editie. Pearson.