Wiskunde

Sandwich Law -uitleg en oefeningen

Sandwich Law -uitleg en oefeningen

De Sandwich Law of tortilla is een methode die het mogelijk maakt om met breuken te werken; In het bijzonder kunt u breuken verdelen. Met andere woorden, via deze wet kunt u divisies rationele getallen maken. De wet van Sandwich is een nuttig en eenvoudig hulpmiddel om te onthouden.

Dit artikel zal alleen worden beschouwd als het geval van de verdeling van rationele getallen die niet beide hele getallen zijn. Deze rationele getallen staan ​​ook bekend als fractionele of gebroken cijfers.

Uitleg

Stel dat u twee fractionele nummers A/B ÷ C/D moet verdelen. De sandwichwet bestaat uit het uiten van deze divisie als volgt:

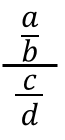
Deze wet stelt vast dat het resultaat wordt verkregen door het aantal aan de bovenkant (in dit geval het nummer "A") te vermenigvuldigen door het lagere end nummer (in dit geval "D"), en deze vermenigvuldiging te delen tussen het product van de product Gemiddelde cijfers (in dit geval, "B" en "C"). De vorige verdeling is dus gelijk aan × D/B × C.

Het kan worden waargenomen in de manier om de vorige verdeling uit te drukken dat de middellange lijn langer is dan die van fractionele getallen. Het wordt ook op prijs gesteld dat het vergelijkbaar is met een sandwich, omdat de tapas de fractionele nummers zijn die u wilt verdelen.

Deze divisietechniek staat ook bekend als de dubbele C, omdat een grote "C" kan worden gebruikt om het product van extreme nummers en een kleinere "C" te identificeren om het product van de mediumnummers te identificeren:

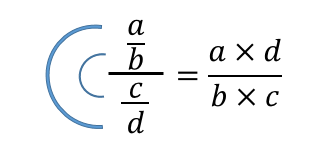
Illustratie

Fractionele of rationele getallen zijn getallen van de M/N -vorm, waarbij "M" en "N" hele getallen zijn. De multiplicatieve omgekeerde van een rationeel nummer M/N bestaat uit een ander rationeel nummer dat, door het te vermenigvuldigen met M/N, resulteert in nummer één (1).

Kan u van dienst zijn: frequentieverdeling: hoe u een tabel kunt maken, bijvoorbeeld, oefening

Deze multiplicatieve inverse wordt aangegeven door (M/N)-1 En het is gelijk aan N/M, omdat M/N × N/M = M × N/N × M = 1. Door notatie moet je ook (m/n)-1= 1/(m/n).

De wiskundige rechtvaardiging van de sandwichwet, evenals andere bestaande technieken om breuken te verdelen, ligt in het feit dat door twee rationele getallen A/B en C/D op de achtergrond te delen, de vermenigvuldiging van A/B is voor de multiplicatieve inverse van C/D. Dit is:

A/B ÷ C/D = A/B × 1/(C/D) = A/B × (C/D)-1= A/B × D/C = A × D/B × C, zoals eerder verkregen.

Om niet meer te werken, is iets waarmee rekening moet worden gehouden voordat de wet van de sandwich wordt gebruikt dat beide breuken zo vereenvoudigd mogelijk zijn, omdat er gevallen zijn waarin het niet nodig is om de wet te gebruiken.

Bijvoorbeeld 8/2 ÷ 16/4 = 4 ÷ 4 = 1. De wet van de sandwich had kunnen worden gebruikt, waardoor hetzelfde resultaat werd verkregen na vereenvoudiging.

Een ander belangrijk ding om te overwegen is dat deze wet ook kan worden gebruikt wanneer een fractioneel getal vereist is door een geheel getal. In dit geval moet een 1 onder het gehele gehele getal worden geplaatst en de wet van de sandwich gebruiken zoals voorheen. Dit komt omdat elk hele nummer K vervult dat k = k/1.

Opdrachten

Hieronder is een reeks divisies waarin de wet van het sandwich wordt gebruikt:

  • 2 ÷ (7/3) = (2/1) ÷ (7/3) = (2 × 3)/(1 × 7) = 6/7.
  • 2/4 ÷ 5/6 = 1/2 ÷ 5/6 = 1 × 6/2 × 5 = 6/10 = 3/5.

In dit geval werden breuken 2/4 en 6/10 vereenvoudigd, die tussen 2 omhoog en omlaag werden gedeeld. Dit is een klassieke methode om breuken te vereenvoudigen die bestaan ​​uit het vinden van de gemeenschappelijke divisors van de teller en de noemer (indien aanwezig) en zowel tussen de gemeenschappelijke deler te delen totdat een onherleidbare fractie is verkregen (waarin er geen gemeenschappelijke scheidaars zijn).

  • (xy+y)/z ÷ (x+1)/z2= (xy+y) z2/z (x+1) = (x+1) yz2/z (x+1) = yz.
Kan u van dienst zijn: evenredigheidsrelaties: concept, voorbeelden en oefeningen

Referenties

  1. Almaguer, g. (2002). Wiskunde 1. Redactionele limusa.
  2. Álvarez, J., Jácome, J., López, J., Cruz, E. D., & Tetumo, J. (2007). Basic Mathematics, Support Elements. Univ. J. Autonoom van Tabasco.
  3. Bails, b. (1839). Principes van rekenkunde. Gedrukt door Ignacio vervuld.
  4. Barker, l. (2011). Lichte teksten voor wiskunde: nummer en bewerkingen. Leraar creëerde materialen.
  5. Barrios, a. NAAR. (2001). Wiskunde 2e. Redactionele progreso.
  6. Eguiluz, m. L. (2000). Fracties: een hoofdpijn? Nieuwe boeken.