Hooke -wetgeving formules, voorbeelden, aanvragen, oefeningen

De Hooke's wet wijst erop dat de vervorming door een elastisch object recht evenredig is met de uitgeoefende kracht erop. De evenredigheidsconstante hangt af van de aard van het object, de geometrie en het materiaal waarmee het wordt vervaardigd.

Alle materialen hebben in meer of mindere mate elastische eigenschappen, dus ze voldoen aan de wet van Hooke wanneer ze terugkeren naar hun oorspronkelijke dimensies, zodra de kracht ophoudt. Elastische bronnen en tandvlees zijn goede voorbeelden van objecten die voldoen aan de wet van Hooke, maar dat geldt ook voor de stalen cabillas die deel uitmaken van een brug.

Figuur 1. Hooke's wet in het voorjaar

Als voorbeeld een veer of dok nemen, om het uitgerekt of gecomprimeerd te houden, is het noodzakelijk om een ​​kracht aan te brengen waarvan de grootte f is. Volgens de wet van Hooke zal de lente een X -vervorming ervaren:

F ∝ x

De evenredigheidsconstante, die, als een veer, wordt genoemd Veerstijfheid, Het wordt daarom aangeduid als k,:

F = K⋅x

In de eenheden van het internationale systeem komt de Force in Newton (N) en de vervorming in meters (M). Daarom heeft de veerconstante N/M -eenheden. De veerconstante vertegenwoordigt de kracht die moet worden uitgeoefend om deze in 1 m lang te vervormen.

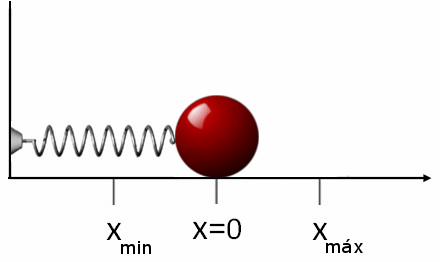Figuur 2. Wanneer de veer wordt uitgerekt, is de kracht die op het object wordt uitgeoefend tegenovergestelde. Hetzelfde gebeurt als de veer krimpt, in dit geval drijft het het object in de tegenovergestelde zin. Bron: Wikimedia Commons.

Als het na het uitrekken of comprimeren van de veer wordt vrijgegeven, zal deze in de tegenovergestelde richting gaan naar de uitgeoefende kracht. Dit betekent dat als we het uitrekken, het wordt gecomprimeerd en vice versa is. Dat is de reden waarom kracht f_R Dat De lente -oefeningen is:

F_R = -k⋅x

Het negatieve teken geeft aan wat er wordt gezegd: dat de kracht zich verzet tegen verplaatsing, dus deze kracht staat bekend als Herstelkracht.

[TOC]

Formule en vergelijkingen

De relatie tussen kracht en verplaatsing in een lente werd ontdekt door Robert Hooke (1635-1703), een opmerkelijke Engelse natuurkundige en bekend om zijn rivaliteit met Isaac Newton. Hooke was een veelzijdige wetenschapper die met succes op verschillende gebieden van de wetenschap heeft gebracht: mechanica, biologie, astronomie en architectuur.

figuur 3. De Engelse natuurkundige Robert Hooke, die geen portretten van die tijd kent. Dit is een wederopbouw van de kunstenaar Rita Gerer in 2004 door beschrijvingen achtergelaten door degenen die de wetenschapper ontmoetten. Bron: Wikimedia Commons. Rita Greer / Fal.

Hooke realiseerde zich dat als de kracht die op een pier wordt uitgeoefend niet erg groot is, het dok evenredig is om te dwingen, en eenmaal deze kracht verdwijnt, heeft de veer weer zijn natuurlijke lengte.

Kan u van dienst zijn: de magnetosfeer van de aarde: kenmerken, structuur, gassen

Op deze manier heeft de wet van Hooke grafisch de vorm van een rechte lijn, waarvan de helling de veerconstante is. De volgende afbeelding toont de kracht die op de veer wordt uitgeoefend om het uit te rekken - of te comprimeren - afhankelijk van de X -positie. Merk op dat de kracht niet afhankelijk is van de natuurlijke lengte van de veer, maar van zijn verplaatsing.

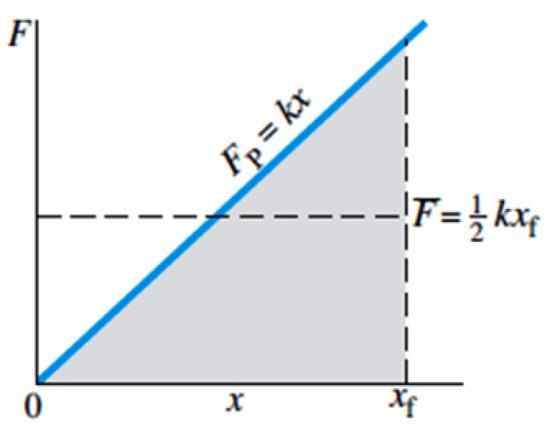Figuur 4. Magnitude F van de noodzakelijke kracht om een ​​veer te strekken of te comprimeren, afhankelijk van de X -vervorming. Bron: Giancoli, D. Fysica met toepassingen.

De gemiddelde kracht wordt aangegeven in de grafiek door F met balk en is gelijk aan ½ kx_F, waar x_F is de uiteindelijke positie van de lente.

Zowel de kracht die in de lente wordt uitgeoefend, en de kracht die hij uitoefent op een object dat aan hem is vastgebonden, zijn variabele krachten. Hoe meer u wilt strekken of comprimeren tot de veer, hoe meer kracht u moet toepassen om het te kunnen bereiken.

Werk gedaan om een ​​veer te strekken of te comprimeren

Wanneer een kracht wordt uitgeoefend die de veer vervormt, wordt een werk dat in het voorjaar is opgeslagen, dat later kan worden gebruikt.

Mechanisch werk wordt gedefinieerd als het gebied onder de grafiek van kracht F afhankelijk van positie X. Om het werk te berekenen W dat een variabele kracht f (x) maakt bij het verplaatsen van een object van positie x₁ Om x te positioneren₂ De gedefinieerde integrale moet worden berekend:

In het geval van het werk dat nodig is om een ​​veer uit zijn evenwichtspositie te brengen om X te positioneren_F Het is heel eenvoudig, omdat het te berekenen gebied is dat van de grijze gearceerde driehoek van figuur 4, waarvan de formule bekend is:

Driehoeksgebied = ½ basis. hoogte

Daarom is het benodigde werk:

W = ½ x_F . (KX_F) = ½ K (x_F))²

En als u het benodigde werk wilt berekenen om naar de veer te brengen vanuit positie X naar positie X_F, Het zou gelijkwaardig zijn aan het berekenen van het gebied van de bekraste trapeze in figuur 5:

W = ½ K (x_F))² - ½ K x²

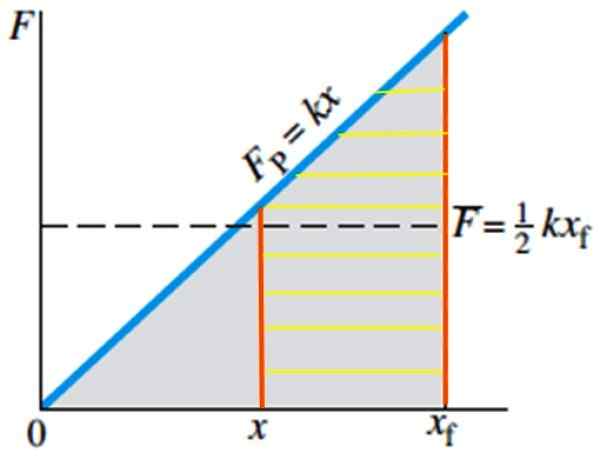Figuur 5. Het werk dat wordt gedaan om de veer te strekken van positie X naar de XF -positie die equivalent is aan het Rayada -gebied. Bron: Giancoli, D. Fysica met toepassingen.

Voorbeelden van veren

Volgens de toepassing waarvoor ze zijn bedoeld, kunnen de veren cilindrisch, conisch, spiraalvormig zijn, met een cirkelvormige dwarsdoorsnede (de meest voorkomende) van vierkante of rechthoekige sectie.

Kan u van dienst zijn: elektrische geleiders

Een veelgebruikte classificatie is afhankelijk van het soort inspanning waaraan ze zullen worden onderworpen: er zijn torsie, flexie, compressie en extensieveren. De laatste worden veelvuldig gebruikt en er werken ook voor spanning en compressie.

Compressieveer

Een voorbeeld van compressieveer is wat wordt gebruikt in het speelgoed dat wordt genoemd Pogo of Saltoín Palo. Deze bronnen slaan een behoorlijk potentiële energie op wanneer ze geleidelijk worden gecomprimeerd en vrijgegeven terwijl ze terugkeren naar de evenwichtspositie. Op deze manier zijn de rebounds niet te abrupt.

Figuur 6. Pogo- of Saltoín -stick is gebaseerd op een compressieveer. Bron: Wikimedia Commons.

Extensie en torsieveren

De veer voor SPRAMPS is het type verlengingsveren en worden vervaardigd met goed gerichte bochten, met twee haken aan de uiteinden. Ze zijn in staat om voldoende potentiële energie te behouden, die ze later vrijgeven wanneer iemand oprijst en begint te springen op het canvas, dat ook hun eigen elastische reactie heeft, zoals alle materialen.

Torsieveren zijn heel gebruikelijk, omdat ze dienen om kledingklemmen te maken. In plaats van haken aan de uiteinden, buigen ze zich in de hoek, om de krachten te weerstaan ​​die de neiging hebben om torsie uit te oefenen.

Figuur 7. De veren maken deel uit van ontelbare mechanismen, zoals deze kledingpincet. Bron: PxFuel.

Materialen voor productieveren

De meest geschikte materialen om veren te maken, zijn die met een Ultieme weerstand (Eindweerstand), dat wil zeggen, ze ondersteunen een grote inspanning voordat ze breken. Het is ook handig dat het materiaal een hoog kruippunt heeft, zodat het zijn elastische kwaliteiten niet verliest met kleine inspanningen.

Industrieel gebruiksveren worden vervaardigd met legeringen die staal met hoge koolstof-, koper-, nikkel- en bronzengehalte omvatten.

Hook's Law -aanvragen

Aangezien de veren de deugd hebben om potentiële energie op te slaan wanneer ze zich uitrekken of comprimeren, kunnen ze werk doen door dingen zoals mechanismen te verplaatsen.

Op deze manier hebben de veren veel toepassingen, van kleine en dagelijkse objecten, via auto's tot machines van allerlei soorten. De bronnen dienen om:

-Schoktrillingen.

-Fabricage intrekbare mechanismen: pen, hangende pincet, haarhaken.

-Maak veer- of dynamometers

En ze maken ook deel uit van het mechanisme van:

Kan u van dienst zijn: gesloten elektrisch circuit

-Horloges.

-Trampolines.

-Sloten.

-Speelgoed.

-Wapens.

-Naaldmeters, bijvoorbeeld de galvanometer, gebruikt om stromen, spanningen en weerstanden te meten.

Opgeloste oefeningen

- Oefening 1

Een kracht van grootte 5 wordt uitgeoefend.0 n bij een veer, met een lengte van 3 stretch.5 cm vanaf de natuurlijke lengte.

a) hoeveel wordt uitgerekt wanneer de uitgeoefende kracht 7 n is?

b) Vind het werk dat wordt gedaan door de uitgeoefende kracht om zich uit te strekken tot lente 3.5 cm vanaf de natuurlijke lengte.

Oplossing voor

Weten dat de veer stretch 3 is.5 cm door de toepassing van 5.0 n We kunnen uw constante berekenen:

K = f / x = 5.0 N / 3.5 cm = 1.43 N / cm.

Wanneer een 7 N -kracht wordt uitgeoefend, wordt het volgende stuk verkregen:

x = f / k = 7.0 N / 1.43 N/M = 4.9 cm

Oplossing B

Het benodigde werk om een ​​veer te vervormen wordt gegeven door:

W = ½ kx² = 0.5 x 1.43 N / cm X (3.5 cm)² = 8.76 n . cm = 8.76 n . 1 x10 ^-2 M = 0.0876 J.

- Oefening 2

Een veer van verachtelijk deeg en 10 cm lang hangt aan een ondersteuning. Als een massa van 2 kg wordt opgehangen, wordt de veer uitgerekt tot het bereikt van 15 cm. Berekenen:

a) de veerconstante

b) De veergrootte wanneer een massa van 3 kg wordt opgeschort.

Oplossing voor

De veerstrek is x = 15 - 10 cm = 5 cm

Aangezien het systeem in statisch evenwicht is, wordt de kracht uitgeoefend door de veer wanneer het uitrekken verticaal omhoog wordt gericht, om het gewicht te compenseren, dat naar beneden wordt gericht, dan:

F_R = W → kx = mg

K = 2 x 9.8 n / 5 x10 ^-2 M = 392 N/M

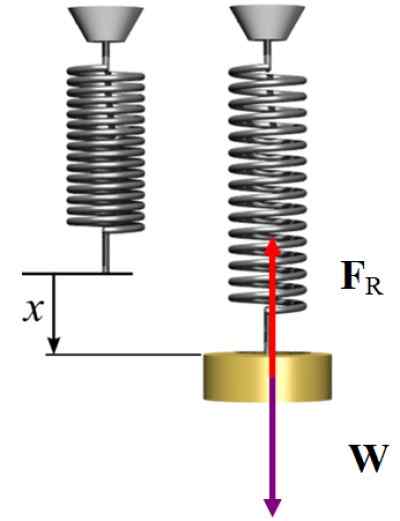Gratis lichaamsdiagram voor de oefening opgelost 2. Bron: Wikimedia Commons/F. Zapata.

Oplossing B

Wanneer een gewicht van 3 kg wordt opgehangen, is de nieuwe kracht W = 3 x 9.8 n = 29.4 n

In dit geval is het stuk:

x = mg /k = 29. 4 N / 392 N / M = 0.075 m = 7.5 cm

Referenties

1. Bauer, W. 2011. Fysica voor engineering en wetenschappen. Deel 1. MC Graw Hill.
2. Creatief mechanismen blog. Vier verschillende soorten bronnen. Hersteld van: creativemechanismen.com.
3. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Deel 2. Dynamisch. Uitgegeven door Douglas Figueroa (USB).
4. Giancoli, D.  2006. Fysica: principes met toepassingen. 6e. ED. Prentice Hall.
5. Ridder, r.  2017. Fysica voor wetenschappers en engineering: een strategiebenadering.  Pearson.