Darcy Law

We leggen uit wat de wet van Darcy, zijn vergelijkingen, toepassingen, beperkingen is en stellen een oefening voor om op te lossen

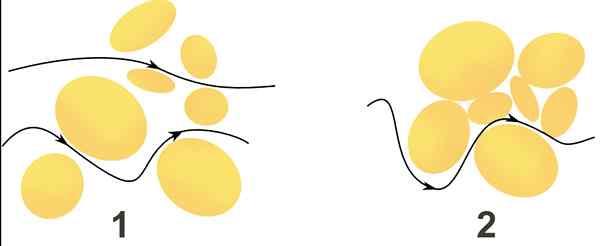
Waterstroom door twee poreuze media wordt aangegeven door zwarte pijlen. In medium 1 beweegt de stroom sneller dan in het middelste 2, omdat de snelheid afhangt van de grootte van de tussenruimten en het gemak van communicatie daartussen. Bron: Wikimedia Commons.

Wat is de wet van Darcy?

De Darcy Law Het is een wiskundige relatie die van toepassing is op de stroom van vloeistoffen in permeabele of poreuze media, bijvoorbeeld het water dat zich in het zand afvoert.

Naarmate de vloeistof door het poreuze vooruitgaat, varieert de hydrostatische druk, met name groter op de punten die het dichtst bij de bron ligt en lager is op de punten die het dichtst bij de afwatering ligt. Op deze manier verschijnt het concept van hydraulische gradiënt, een fysieke hoeveelheid die zal worden aangegeven met de letter i.

Aan de andere kant wordt het poreuze medium gekenmerkt door een hoeveelheid die wordt genoemd Hydraulische geleidbaarheid K. Er is duidelijk een verband tussen de porositeit, bepaald door K, de hydraulische gradiënt I en de stroom per eenheid van dwarsdoorsnede Q Q.

De relatie tussen hen werd ontdekt door de Franse hydraulische ingenieur Henry Darcy (1803-1858), die de leiding had over de watervoorziening van zijn geboortestad: Dijon.

Darcy's wet werd gepresenteerd in 1856, in een grondig werk waarin de fysieke hoeveelheden die bij de wet betrokken zijn gedetailleerd zijn, de experimenten uitgevoerd en heel in het bijzonder een apparaat genaamd permeter.

Darcy Law -vergelijkingen

Darcy's wet toont de relatie tussen verschillende fysieke hoeveelheden die de stroom door een poreus medium beschrijven. Het geeft aan dat de waterstroom Q die door een bepaald poreus middel beweegt, is recht evenredig met de doorboord van de dwarsdoorsnede en de hydraulische gradiënt Je:

Q ∝ a ∙ i

Kan u van dienst zijn: uniforme rechtlijnige beweging: kenmerken, formules, oefeningen

De evenredigheidsconstante is de permeabiliteit K van de poreuze omgeving, ook wel genoemd Hydraulische geleidbaarheid. Op deze manier wordt de wet van Darcy gepresenteerd als:

Q = k ∙ a ∙ i

Differentiële vorm van de wet van Darcy

Darcy's vergelijking kan worden uitgedrukt als een differentiaal verband tussen de stroomsnelheid op elk punt en de lokale hydraulische gradiënt:

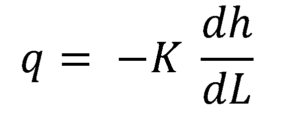
Aangezien de hydraulische gradiënt een negatieve hoeveelheid is wanneer berekend in de richting van de stroom, is het dan nodig om te vermenigvuldigen met het negatieve van de hydraulische geleidbaarheid om de gemiddelde debiet Q te verkrijgen, in elke dwarsdoorsnede.

Dan worden de grootten die aanwezig zijn in de wet van Darcy in meer detail geanalyseerd.

Stroming, hydraulische gradiënt en permeabiliteit

1.- Flow Q

De stroom wordt gedefinieerd als het volume water dat door een bepaald gebied van dwarsdoorsnede circuleert naar de richting van de stroom, per tijdseenheid:

Q = ΔV / Δt

In het internationale systeem van SI -eenheden wordt de stroom gemeten in kubieke meter per seconde, maar deze wordt vaak uitgedrukt in liters per minuut of liters per seconde.

De stroom per eenheid Q -gebied is vaak vereist, wat de verhouding is tussen de Q -stroom en de dwarsdoorsnede:

Q = q / a

In de SI wordt Q uitgedrukt in m/s, daarom vertegenwoordigt Q de gemiddelde snelheid van de vloeistof in de dwarsdoorsnede van de pijp.

Het is belangrijk op te merken dat, hoewel de stroom Q hetzelfde is in alle secties van de pijp, de stroom per eenheid van gebied Q of eenvoudigweg het debiet hoger is in de smalste en kleinere secties in de bredere secties.

2.- Hydraulische gradiënt i

Wanneer een vloeistof circuleert langs een poreus medium, neemt de hydrostatische druk af in dezelfde richting van de stroom.

Kan u van dienst zijn: ton: transformaties, gelijkwaardigheid en oefeningen opgelost

Het is bekend dat de hydrostatische druk, op een bepaald punt in de pijp, evenredig is met de hoogte H die een open buisdrukmeter op die plaats markeert. De evenredigheidsconstante is het product van vloeistofdichtheid als gevolg van zwaartekrachtversnelling.

Op deze manier wordt de hydraulische gradiënt I gedefinieerd als de verhouding tussen het hoogteverschil ΔH van de kolommen van twee manometers en AL, de laatste is de afstand die de manometers scheidt (zie de onderstaande figuur):

I = ΔH / Δl

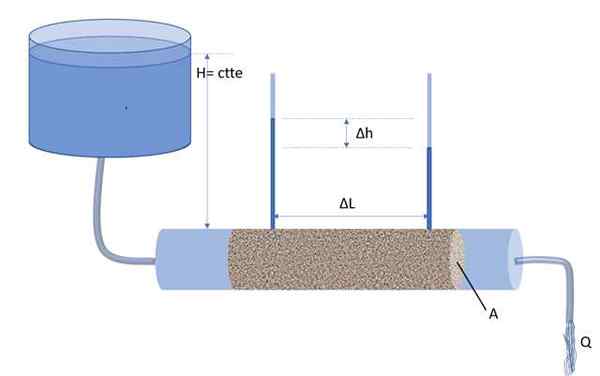De permemeter, een apparaat uitgevonden door Henry Darcy om de waterstroom door een poreus medium te kwantificeren. Bron: f. Zapata.

Dit is de gemiddelde hydraulische gradiënt in het gedeelte van lange AL, een dimensieloze hoeveelheid en ook negatief.

Als u de hydraulische gradiënt op elk punt in de pijp wilt vinden, wordt de limiet genomen voor AL die neigt naar nul, wat resulteert in de afgeleide van de hydraulische gradiëntfunctie ten opzichte van de positie L, langs de stroom:

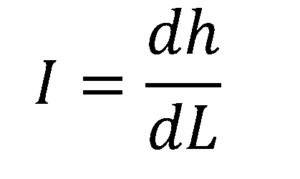
3.- Permeabiliteit k

De permeabiliteit van een poreuze gemiddelde of hydraulische geleidbaarheid is de verhouding tussen de stroom Q en het product van de dwarsdoorsnede NAAR Voor de hydraulische gradiënt Je:

K = q / a ∙ i

Hydraulische geleidbaarheid heeft snelheidseenheden, meters boven zichzelf.

Een eenheid voor k is gedefinieerd, genaamd Darcy, Ter ere van Henry Darcy en als volgt gedefinieerd:

A Darcy Het is de permeabiliteit van een vloeistofmilliliter, met een viscositeit van een centipoise, die langs een centimeter beweegt in een differentiële druk van een atmosfeer, door een dwarsdoorsnede van een vierkante centimeter.

Darcy Law -aanvragen

De belangrijkste toepassing van de wet van Darcy is om de waterstroom langs een watervoerende laag te voorspellen, voordat ze putten boren.

Kan u van dienst zijn: dimensionale analyse

Ook wordt de wet van Darcy regelmatig gebruikt in agrarische en hydrologische engineering. Het kan ook worden gebruikt in de olie -industrie om de stroom van gas en olie in poreuze media te beschrijven. In dat geval kan K echter variëren, afhankelijk van de stroom van gas of olie en kan het mogelijk niet alleen en exclusief afhangen van het permeabele substraat.

Beperkingen

De wet van Darcy gaat ervan uit dat de hydraulische geleidbaarheid K een hoeveelheid van het medium is, wat in veel gevallen waar is. Soms hangt K echter af van de dynamische viscositeit van de vloeistof, die op zijn beurt kan afhangen van de stroomsnelheid en temperatuurgradiënten.

Darcy's veronderstelling is aannemelijk bij het overwegen van ondergronds water, waar viscositeit praktisch constant is, omdat de waarde ervan bijna niet wordt beïnvloed met het oog op de weinige temperatuurverschillen in de aquifer.

In gevallen van oliestroom door poreuze middelen kan de Darcy -vergelijking niet worden toegepast zoals hier gepresenteerd, maar bepaalde wijzigingen worden opgenomen die verder gaan dan het doel van dit artikel.

Oefening opgelost

Bepaal de hydraulische geleidbaarheid van een strandzand, door een laboratoriumpermemeter te gebruiken.

Stel dat de permeterbuis een diameter van 20 cm heeft en dat de afstand tussen de twee manometers 50 cm is. Het is ook bekend dat water stroomt met een snelheid van 300 kubieke decimeters per minuut en het niveauverschil tussen de twee manometers is 25 cm.

Oplossing

De stroom die 300 kubieke decimeters per minuut is, maar in eenheden van het internationale systeem uiten, zou het zo zijn:

Q = 300 x 10^-3 M³ / 60 s = 5 x 10^-3 M³ / S

De dwarsdoorsnede A wordt berekend door:

A = π ∙ r² = π ∙ (10 cm)² = π ∙ (0,1 m)² = 0,314 m²

Hydraulische gradiënt I is een quotiënt tussen het manometrische hoogteverschil en de scheiding van de manometers:

I = 25 cm / 50 cm = 0,5

Volgens de definitie van hydraulische geleidbaarheid k hierboven gegeven:

K = q / a ∙ i = (5 x 10^-3 M³ / s) / (0,314 m² ∙ 0,5) = 3.185 x 10^-2 m/s ≈ 2 m/min.