Homologe kanten

We leggen uit wat de homologe kanten zijn, met voorbeelden en oefeningen opgelost

Wat zijn homologe kanten?

De homologe kanten In twee vlakke geometrische figuren zijn die die met elkaar overeenkomen, waarbij de gelijkenis behouden. De rechterhand van een persoon is bijvoorbeeld homoloog met de rechterhand van een ander.

In vlakke geometrie zijn er niet alleen homologe kanten, maar ook hoekpunten en homologe hoeken. Om het te zien, overweeg de volgende figuur, die bestaat uit twee identieke driehoeken ABC en a'b'c ':

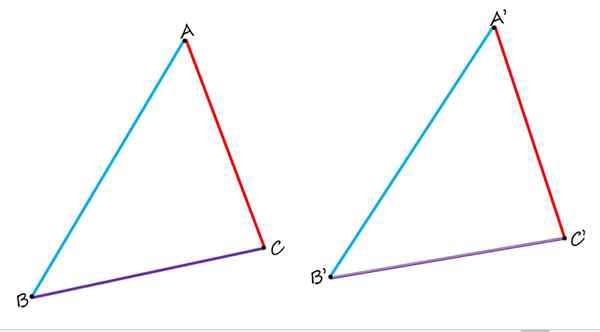
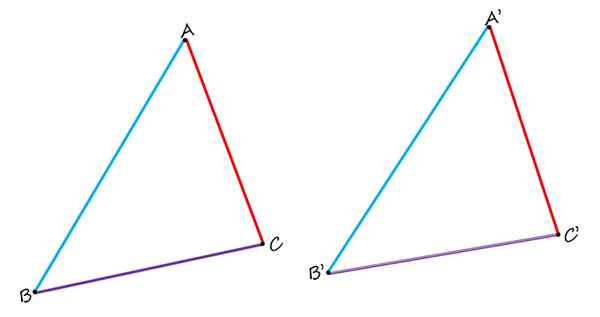In de twee identieke driehoeken zijn de AB en A'B 'homoloog, evenals zijden BC en B'c' en AC en A'C '. Bron: f. Zapata.

Bij het vergelijken ervan wordt duidelijk waargenomen dat de zijkanten ab en a'b 'in blauw homoloog zijn, omdat ze een vergelijkbare positie innemen in elke driehoek. De zijden BC en B'c 'in Purple zijn ook homoloog. En ten slotte is de rode AC -kant homoloog aan de zijkant a'c '.

Uitleg

Uit het bovengenoemde volgt hieruit dat de homologe kanten die zijn die dezelfde relatieve positie innemen in figuren op dezelfde manier. In het vorige beeld werden twee identieke driehoeken gebruikt om het idee te tonen, maar dit kan gemakkelijk andere platte geometrische figuren generaliseren, gevormd door opeenvolgende zijden die sluiten.

Deze cijfers worden genoemd polygonen. Driehoeken en vierhoeken zijn bijvoorbeeld polygonen van respectievelijk 3 en 4 zijden.

Het concept van homologe kanten is belangrijk omdat het mogelijk maakt om criteria van gelijkenis tussen polygonen te definiëren, zoals binnenkort zal worden gezien. De vergelijkbare cijfers hebben exact dezelfde vorm en houden een identieke verhouding tussen hun zijden, zelfs als ze niet dezelfde grootte hebben.

En hoewel tot nu toe alleen naar vlakke cijfers werd verwezen, zijn er ook vergelijkbare cijfers in drie dimensies. Ze worden gemakkelijk waargenomen in schappen van de supermarkt, wanneer hetzelfde product in identieke containers wordt verkocht, maar met een andere grootte.

Kan u van dienst zijn: wiskundige logica

Andere woorden die door elkaar worden gebruikt in geometrie om te verwijzen naar homologe zijden in geometrische figuren zijn: overeenkomstige zijden, respectieve zijden en equivalente zijden.

Homologe hoekpunten en hoeken

Net als bij de zijkanten worden ook homologe hoekpunten gedefinieerd, die paren van homologe kanten verenigen. Vertices A en 'uit de vorige figuur zijn bijvoorbeeld homoloog. Evenzo zijn de paren van hoekpunten B en B 'en C en C' homoloog.

Ten slotte nemen homologe hoeken dezelfde relatieve positie in in de figuren. De hoekpunten van homologe hoeken zijn op hun beurt homoloog.

Om het idee te illustreren, neemt u de hoek tussen de blauwe en paarse zijden van de linker driehoek, die kan worden aangeduid als ∠abc. Deze hoek heeft zijn tegenhanger onder de hoek ∠a'b'c ', van de driehoek aan de rechterkant.

Het hoekpunt van deze hoek is B, zoals eerder aangegeven, een tegenhanger is met B ', en de andere twee paren van homologe hoeken van de getoonde driehoeken zijn:

• ∠bca en ∠b'c'a '
• ∠cab en ∠c'a'b '

Gelijkenis van polygonen

Voor twee polygonen die vergelijkbaar zijn, moeten aan de volgende voorwaarden worden voldaan:

• Alle paren homologe hoeken hebben dezelfde maatregel
• Zijn paren van homologe kanten zijn evenredig.

De twee voorwaarden moeten tegelijkertijd worden voldaan om gelijkenis te garanderen. Er wordt onmiddellijk waargenomen waarom.

In de volgende figuur zijn er twee vierhoekige vierzalen die duidelijk niet vergelijkbaar zijn. Het is te wijten aan het feit dat de eerste status van wekelijks wordt vervuld, maar de tweede niet:

Twee vierhoekige vierkanten die niet vergelijkbaar zijn, hoewel hun homologe hoeken gelijke maatregelen hebben. Bron: f. Zapata.

Terwijl in de figuren hun paren homologe hoeken dezelfde maat hebben, omdat ze allemaal rechte hoeken zijn (ze meten 90º), zijn de cijfers niet vergelijkbaar, omdat hun paren geen evenredig zijn.

Kan u van dienst zijn: injectieve functie: waar het uit bestaat, waarvoor is het en voorbeelden

Aan de andere kant hebben deze twee vierhoekige zijden met gelijke mate homologe kanten, maar de homologe hoeken meet niet hetzelfde. Daarom zijn cijfers duidelijk niet vergelijkbaar.

Twee vierhoekige vierzijdige zijden van dezelfde maat, maar met verschillende interne hoeken, daarom zijn het geen vergelijkbare figuren. Bron: f. Zapata.

Gelijkenis reden

Als twee cijfers vergelijkbaar zijn, is het quotiënt tussen de homologe zijden hetzelfde en wordt het genoemd gelijkenis reden.

De zijkanten van een van de figuren zoals A, B, C, D ... en de overeenkomstige figuur aangeven als A ', B', C ', D

Perimeters en gebieden van soortgelijke cijfers

De gelijkenisverhouding maakt het mogelijk om relaties tussen de perimeters, gebieden en volumes van twee vergelijkbare figuren te verkrijgen.

Perimeter reden voor twee vergelijkbare cijfers

De perimeter P van een polygoon wordt gedefinieerd als de som van al zijn zijden. Als je een figuur hebt waarvan de zijkanten A ', B', C ', D' ... zijn ..., is de perimeter P ':

P '= a' + b ' + c' + d '.. .

Als een andere polygoon vergelijkbaar is met dit, en zijn zijden A, B, C, D ..., is het vervuld dat:

En daarom:

A = r ∙ a '

U kunt hetzelfde bevestigen voor de andere kanten van deze figuur. Dus de omtrek P wordt uitgedrukt als:

P = A + B + C + D .. . = R ∙ A ' + R ∙ B' + R ∙ C ' + R ∙ D' +…

Omdat "R" een gemeenschappelijke factor is voor alle verslaafden, is de relatie tussen P en P ':

P = r ∙ p '

Dit betekent dat de reden voor de perimeters tussen twee vergelijkbare polygonen gelijk is aan de reden voor gelijkenis.

Reden voor gebieden van twee vergelijkbare cijfers

Als twee vergelijkbare cijfers respectievelijk gebieden A en A 'hebben, zijn deze gerelateerd door:

Kan u van dienst zijn: Formula -opruimingsoefeningen

A = r²∙ A '

Waarbij "r" de reden is voor gelijkenis van de cijfers.

Volumeverhouding van twee vergelijkbare cijfers

Het zijn twee vergelijkbare drie -dimensionale figuren, waarvan de volumes respectievelijk V en V 'zijn. De relatie tussen hen, via "R" is:

V = r³∙ V '

Voorbeelden

Blauwdrukken

Delen van een land, de plant van een gebouw of zelfs een kledingstuk, op een kleinere schaal op een vel papier kunnen worden weergegeven. De plannen hebben het voordeel dat ze ermee kunnen meenemen en de relevante wijzigingen gemakkelijk kunnen aanbrengen, voordat ze op het echte object in de praktijk worden gebracht.

Kaarten

Het zijn meestal representaties in het vlak van een groot landgebied, van een dorp tot de continenten. Ze zijn ook op een bepaalde schaal gemaakt.

Ze hebben talloze toepassingen en er zijn veel soorten. Via een kaart kan het terrein bijvoorbeeld worden beschreven, en wanneer het zich op een specifiek punt bevindt, wordt de beste route om van dat punt naar een andere te gaan, bepaald.

Modellen

Het zijn drie -dimensionale representaties op de schaal van objecten zoals auto's, gebouwen en constructies in het algemeen.

Oefening opgelost

De volgende waarden komen overeen met de zijkanten van een paar vergelijkbare driehoeken. Vind de reden voor gelijkenis en waarden van "X" en "Y":

Driehoek 1: 5, 8, 10

Driehoek 2: 150, x, y

Oplossing

De reden voor gelijkenis is het quotiënt:

R = 150/5 = 30

Daarom:

x = 30 × 8 = 240

y = 10 × 30 = 300