Geschiedenis van trigonometrie uit zijn oorsprong

De Trigonometrie geschiedenis Het verwijst naar de reeks feiten en vooruitgang die zich voordeden rond deze tak van wiskunde van zijn oorsprong tot de meest recente gebeurtenissen.

Bij het maken van een korte reis door zijn geschiedenis, is het duidelijk dat deze wetenschap is geboren als reactie op de problemen waarmee de oude astronomen en navigators worden geconfronteerd om de verplaatsing van de sterren in de lucht te analyseren.

De term verschijnt voor het eerst in het boek Trigonometriae Libri Quinque, geschreven door de Duitse wiskundige en wetenschapper Pitiscus Bartolomé (1561-1613). Via Wikimedia Commons.

Evenzo komt het woord trigonometrie voort uit de samenstelling van twee Griekse woorden: Trigonon (driehoek) en Metron (omvang). De term verschijnt voor het eerst in het boek Trigonometriae Libri Quinque, Geschreven door de Duitse wiskundige en wetenschapper Pitiscus Bartolomé (1561-1613).

Op deze manier laat de etymologie van het woord zien dat trigonometrie de studie is de relaties tussen de hoeken van een driehoek en de segmenten of lijnen die het vormen.

[TOC]

Het begin van trigonometrie

De eerste stappen van de trigonometrie werden uitgevoerd door de mens wanneer ze worden gepromoot door de noodzaak om de beweging van de sterren te kennen en te analyseren.

Dat wil zeggen, de mens bedacht trigonometrie omdat het werd gevonden in situaties waarin het onmogelijk was om direct metingen te doen, omdat om de sterren te berekenen, complexere wiskundige hulpmiddelen vereist waren.

- Studies in Babylon

Moddertafel geschreven door die van Babyloniërs genaamd Plimpton 322. Via: Wikimedia Commons

Studies tonen aan dat meer dan 3 geleden.000 jaar Babyloniërs hebben al het concept van hoek en trigonometrische redenen afgehandeld, dat wil zeggen dat ze de relaties tussen de zijden en de hoeken van de driehoeken konden vestigen.

Bijvoorbeeld, een moddertafel - geschreven door die van Babyloniërs - genoemd Plimpton 322 (1800 A. C.) toont een opeenvolging van kolommen en rijen die getallen bevatten in spijkerschrift schrijven. Volgens onderzoek dat door sommige experts is uitgevoerd, vertegenwoordigt deze tablet wat een reeks trigonometrische functies lijkt te zijn.

Kan u van dienst zijn: wat is de richtlijn? (Geometrie)

De Babyloniërs waren bekend met de concepten die aanleiding gaven tot de stelling van Pythagoras (569-474 a.C) en zij begrepen hun principe.

Op dezelfde manier wisten ze ook de stelling die werd toegeschreven aan de thales van Miletus (695-546 tot.C), dat aangeeft dat elke rechte, parallel aan de zijkant van een driehoek, vormt met de andere twee zijden een andere driehoek die vergelijkbaar is met de eerste driehoek.

- De oude Egyptenaren

De oude Egyptenaren slaagden erin om de helling uniform te behouden op elk van de piramide -gezichten. Via: Pixabay

Hoewel het niet gepast is om te praten over trigonometrie in de algemene sfeer van de Egyptische wiskunde, is er geen twijfel dat deze beschaving bepaalde trigonometrische concepten heeft behandeld.

Dit gebeurt omdat bij het overwegen van de grote gebouwen van de Egyptenaren, zoals piramides, kan worden geconcludeerd dat ze enige kennis hadden over trigonometrie.

Een basistechnische moeilijkheid waarmee de Egyptenaren worden geconfronteerd - en dat loste verbazingwekkend op.

Hiervoor gebruikten ze een concept dat ze "seqt" noemden en dat is gelijk aan wat we vandaag begrijpen als een helling van een hellend plat oppervlak.

Bovendien zijn de Egyptenaren om metingen te doen op de verticale oppervlakken die als een eenheid worden gebruikt, de "elleboog" en in de horizontaal de "hand", die overeenkwam met 1/7 van de elleboog. Op deze manier berekenden ze de seqt of in behandeling in de verschillende gebouwen. Bijvoorbeeld, in de piramide van jufú (queope) is de seqt 5 1/2 handen per elleboog.

- Oude Griekenland en de snaartafel

Alle kennis van de Babyloniërs en de oude Egyptenaren passeerden Griekenland, waar de wiskundige en astronoom van Nicea (190-120 werd benadrukt (190-120. C), dat wordt beschouwd als de vader van trigonometrie. Hiparco creëerde de tafels van de "strings", waarmee hij de problemen van platte driehoeken oplost.

Nicea Hiparco - Bron: overgedragen van.Wikipedia to Commons van Maksim - onder Public Domain

Om ze te maken, gebruikte het een omtrek met een bepaalde straal (een straal is de afstand tussen het midden van een cirkel en elk punt van de omtrek).

Kan u van dienst zijn: voorwaardelijke waarschijnlijkheid: formule en vergelijkingen, eigenschappen, voorbeelden

Toen verplaatste het de straal om verschillende hoeken te definiëren; Terwijl dit deed, wees in de tabel de lengte van de lijn die werd afgebakend aan de zijkanten van de hoek en de omtrek.

Deze "snaren" bleken de voorlopers te zijn van de tafels van de trigonometrische functies die we vandaag gebruiken.

- India -bijdragen

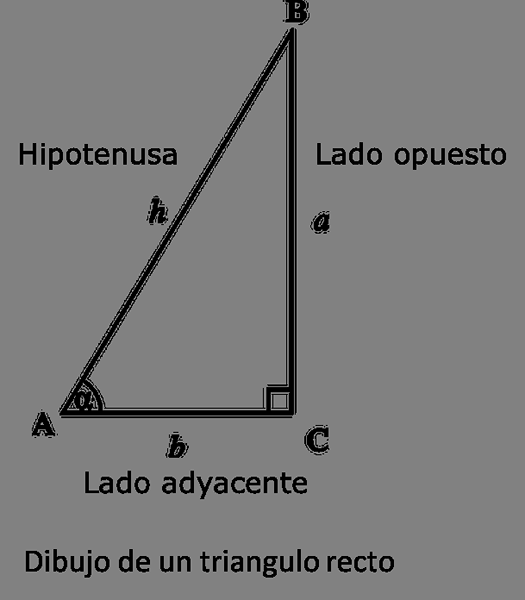Tekening van een rechter driehoek.

Net als Griekenland geleerden ontwikkelden astronomen van India ook een trigonometrisch systeem, maar in tegenstelling tot de Grieken baseer deze astronomen hun analyse op de "sinus" -functie in plaats van de strings te gebruiken.

De "sinus" -functie die door deze astronomen wordt uitgedrukt, is echter niet degene die tegenwoordig wordt gebruikt; Deze functie was geen aandeel (zoals vandaag gebruikt), maar de lengte van de andere kant van een hoek van een rechthoekige driehoek waarvan de hypotenusa bekend is.

- Arabië en trigonometrische functies

Aan het einde van de achtste eeuw begonnen Arabische astronomen, beïnvloed door trigonometrische studies die werden uitgevoerd door de volkeren van Griekenland en India, belangrijke studies naar relaties tussen hoeken en hun zijden.

Op deze manier verhoogden ze aan het einde van de 10e eeuw de goed bekende functies van borst, cosinus, raaklijn, cotangent, drogen en oogst.

Ze ontdekten en geverifieerde primaire trigonometrie -stellingen, die worden gebruikt bij de analyse van platte en bolvormige driehoeken. Bovendien suggereerden Arabische wiskundigen het gebruik van één waarde ("1") voor radio (r = 1), die aanleiding gaf tot moderne waarden van trigonometrische functies.

- Bijdragen uit het westen

Johann Müller bekend als Regiomontanus (1436-1476). Bereikte systematisering en generalisatie van trigonometrische methoden die in het geometriegebied worden gebruikt. Via: Wikimedia Commons

De wiskunde van het Westen, met name tussen de twaalfde en vijftiende eeuw, werd sterk beïnvloed door de postulaten van het oude Griekenland, India en de Arabieren.

Kan u van dienst zijn: chikwadraat (χ²): distributie, hoe het wordt berekend, voorbeelden

Gedurende deze tijd waren ze beslissend op het gebied van trigonometrie-de bijdragen van Johann Müller, ook bekend als Regiomontanus (1436-1476). Deze wiskundige bereikte de systematisering en generalisatie van trigonometrische methoden die in het geometriegebied worden gebruikt.

Regiomontanus ging uit en publiceerde een verdrag dat hij noemde Van Triangulis Omnimodis Libri Quinque, die bestond uit vijf boeken en in totaal 131 pagina's.

In dit boek reguleerde hij alle concepten van platte en bolvormige trigonometrie, die vervolgens werden gebruikt door belangrijke astronomen zoals: Nicolás Copernic.

- Trigonometrie zeventiende en achttiende eeuw

Tijdens de zeventiende eeuw bleven de studies naar trigonometrische berekeningen voorspoedig zijn dankzij de bijdragen van wiskundigen zoals de Scotch John Napier (1550-1617), die verschillende methoden verhoogden voor de resolutie van sferische driehoeken.

John Napier. Bron: door Encard door Samuel Freeman (1773-1857) [Public Domain], via Wikimedia Common

Later, in de 18e eeuw, waren de bijdragen van de Zwitserse wiskundige Leonhard Euler (1707-1783) beslissend, omdat zijn studies de basis legden van moderne trigonometrie door de notatie te introduceren die momenteel wordt gebruikt voor trigonometrische functies.

Bovendien slaagde Euler erin de exponentiële functie te definiëren en ontdekte zijn relatie met trigonometrische functies, waardoor hij de kenmerken van trigonometrie kon beschrijven.

Vervolgens vergemakkelijkte Sir Isaac Newton (1643-1727), door de differentiële en integrale calculus uit te vinden, de weergave van een groot aantal wiskundige functies, waaronder trigonometrisch. Op deze manier werd trigonometrie onderdeel van de wiskundige analyse, waar tegenwoordig een fundamentele rol speelt.

Illustratie van Sir Isaac Newton

Referenties

1. Mansfield, Daniel. Wildberger, n. (2017). Plimpton 322 is Babylonische exacte seksuele trigonometrie. Opgehaald op 20 mei 2020 van: Scientedirect.com
2. Jimenez S. (2017). Geschiedenis van trigonometrie en zijn toepassingen. Ontvangen op 23 mei 2020 Deedu
3. Pérez, V. (2010). Trigonometrie geschiedenis. Ontvangen op 22 mei 2020 van: Laguia2000.com
4. S.NAAR. (S.F.)) Trigonometrie. Opgehaald op 23 mei 2020 van: Blogspot.com
5. Merlet, Jean-Pierre (2004). Een opmerking over de geschiedenis van trigonometrische functies. Opgehaald op 22 mei 2020 van: NET
6. Adamek, t., Penkalski, K., Valentine, g. (2005). De geschiedenis van trigonometrie. Opgehaald op 23 mei 2020 van: Citseseerx.IST.PSU.Edu/