Heptadecágono -eigenschappen, diagonalen, perimeter, gebied

Hij Heptadecágono Het is een gewone polygoon van 17 zijden en 17 hoekpunten. De constructie ervan kan worden gedaan in de Euclidian -stijl, dat wil zeggen alleen de regel en het kompas gebruiken. Het was het grote genie van de wiskunde Carl Friedrich Gauss (1777-1855), die slechts 18 jaar oud was, die de procedure voor de bouw ervan in 1796 vonden. 

Blijkbaar voelde Gauss altijd erg geneigd tot deze geometrische figuur, tot het punt dat hij vanaf de dag dat hij zijn constructie ontdekte, besloot om wiskundige te zijn. Er wordt ook gezegd dat hij wilde dat de Heptadecágono op zijn grafsteen zou worden opgenomen.

Figuur 1. Heptadecágono is een gewone polygoon van 17 zijden en 17 hoekpunten. Bron: f. Zapata.

Gauss heeft ook de formule gevonden om te bepalen welke reguliere polygonen de mogelijkheid hebben om met regel en kompas te worden gebouwd, omdat sommigen geen exacte Euclidische constructie hebben.

[TOC]

Kenmerken van Heptadecágono

Wat betreft de kenmerken ervan, zoals elke polygoon, is de som van zijn interne hoeken belangrijk. In een normale polygoon van N partij, de som wordt gegeven door:

Sa (n) = (n -2) *180º.

Voor de Heptadecágono het aantal kanten N is 17, Wat betekent dat de som van zijn interne hoeken is:

SA (17) = (17 - 2) * 180º = 15 * 180º = 2700º.

Deze som, uitgedrukt in radianen is als volgt:

Sa (17) = (17 - 2) * π = 15 * π = 15π

Uit de vorige formules kan gemakkelijk worden afgeleid dat elke interne hoek van een heptadecágono een exacte α -maat heeft gegeven door:

α = 2700º/17 = (15/17) π radianen

Hieruit volgt dat de interne hoek ongeveer is:

α ≈ 158,824º

Diagonalen en perimeter

Diagonaal en perimeter zijn andere belangrijke aspecten. In elke polygoon is het aantal diagonalen: 

D = n (n - 3) / 2 en in het geval van Heptadecágono, zoals N = 17, Je moet D = 119 diagonalen.

Kan u van dienst zijn: Trinomial

Aan de andere kant, als de lengte van elke zijde van de Heptadecágono bekend is, dan voegt de omtrek van de reguliere Heptadecágon gewoon 17 keer die lengte toe, of wat 17 keer gelijk is aan de lengte D Aan elke kant:

P = 17 D

Perimeter van Heptadecágono 

Soms is alleen radio bekend R van de heptadecágono, dus het is noodzakelijk om een ​​formule voor deze zaak te ontwikkelen.

Daartoe, het concept van Apothem. Apotheme is het segment dat van het midden van de reguliere polygoon naar het middelpunt aan één kant gaat. De apothem ten opzichte van de zijkant staat loodrecht op die kant (zie figuur 2).

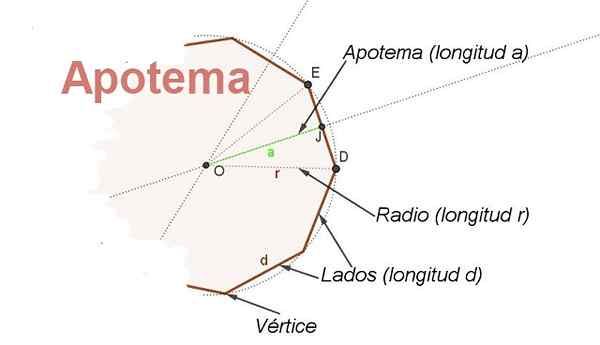Figuur 2. De delen van een normale radio R -polygoon en zijn apothem worden getoond. (Eigen uitwerking)

Bovendien is de apothem bissector van de hoek met centraal hoekpunt en zijden op twee opeenvolgende hoekpunten van de polygoon, dit maakt het mogelijk om een ​​relatie tussen de radio te vinden R en de zijkant D.

Als het wordt gebeld β naar de centrale hoek Doen En rekening houdend met die apothem Oj is bissector die je hebt Ex = d/2 = r sen (β/2), waar je een relatie hebt om de lengte te vinden D aan de zijkant van een polygoon bekend zijn radio R en zijn centrale hoek β:

D = 2 r sin (β/2)

In het geval van Heptadecágon β = 360º/17 Voor wat je hebt:

D = 2 r sen (180º/17) ≈ 0.3675 r

Ten slotte wordt de formule van de omtrek van de Heptadecágono bekend dat de straal ervan is verkregen:

P = 34 R Sen (180º/17) ≈ 6.2475 r

De omtrek van een heptadecágonon Pcir = 2π r ≈ 6.2832 r.

Gebied

Om het gebied van Heptadecágono te bepalen, zullen we verwijzen naar figuur 2, die de zijkanten en de apothem van een gewone polygoon van toont van N zijkanten. In die figuur de driehoek EOD Het heeft een gebied dat gelijk is aan de basis D (polygoonzijde) op hoogte naar (Polygon apothem) gedeeld door 2:

Het kan u van dienst zijn: serie Power: Voorbeelden en oefeningen

EOD = (d x a) / 2

Dus dat bekende apotheme naar van de heptadecágono en de zijkant D van hetzelfde is:

Heptadecágono Area = (17/2) (D X A)

Gebied gegeven de zijkant

Om een ​​formule te krijgen voor het Heptadecágono -gebied dat de lengte van zijn zeventien zijden kent, is het noodzakelijk om een ​​relatie tussen de apotheme lengte te bereiken naar en de zijkant D.

In verwijzing naar figuur 2 heeft u de volgende trigonometrische relatie:

Tan (β/ 2) = EG/ oj = (d/ 2)/ a, wezen β naar de centrale hoek Doen. Dus die apothem naar kan worden berekend als de lengte bekend is D Vanaf de polygoonzijde en de centrale hoek β:

A = (d/2) cotan (β/2)

Als deze uitdrukking voor Apothem nu wordt vervangen, in de formule van het Heptadecágono -gebied verkregen in de vorige sectie, hebt u:

Heptadecágono Area = (17/4) (D²) Cotan (β/2)

Wezen β = 360º/17 Voor de Heptadecágono, dus je hebt eindelijk de gewenste formule:

Heptadecágono Area = (17/4) (D²) Cotan (180º/17)

Gebied gegeven de radio

In de vorige paragrafen was een relatie tussen de D -zijde van een gewone polygoon en zijn R -radio R gevonden, het volgende wezen: het volgende: het volgende wezen:

D = 2 r sin (β/2)

Deze uitdrukking voor D Het wordt geïntroduceerd in de uitdrukking verkregen in de vorige sectie voor het gebied. Als de relevante substituties en vereenvoudigingen worden gemaakt, wordt de formule waarmee het Heptadecágono -gebied wordt verkregen verkregen:

Heptadecágono -gebied = (17/2) (r²) Sin (β) = (17/2) (r²) Sen (360º/17)

Een geschatte uitdrukking voor het gebied is:

Heptadecágono -gebied = 3.0706 (r²)) 

Zoals verwacht, is dit gebied iets minder dan het gebied van de cirkel die omschrijft naar de Heptadecágon NAAR_Circel = π r² ≈ 3.1416 r². Om precies te zijn, het is 2% lager dan die van zijn omschreven cirkel.

Kan u van dienst zijn: gebied van een gewone en onregelmatige Pentagon: hoe het wordt genomen, oefeningen

Voorbeelden

voorbeeld 1

Voor een heptadecágono om 2 cm zijden te hebben, welke waarde moet de straal en diameter van de omschreven omtrek hebben? Vind ook de omtrekwaarde.

Om de vraag te beantwoorden, is het noodzakelijk om de relatie tussen de zijkant en de straal van een gewone polygoon van N -zijden te onthouden:

 D = 2 R Sen (180º / N)

Voor Heptadecágono N = 17, vandaar D = 0.3675 R, Met andere woorden

10.8844 cm in diameter.

De perimeter van een 2 cm zijde Heptadecágon is P = 17* 2 cm = 34 cm.

Voorbeeld 2

Hoeveel is het gebied van een gewone Heptadecágono de 2 cm -kant?

Het is noodzakelijk om te verwijzen naar de formule die wordt aangetoond in de voorgaande sectie, waardoor het gebied van een heptadecágono het kan vinden wanneer de lengte is D Aan zijn zijde:

Heptadecágono Area = (17/4) (D²) / Tan (180º / 17) 

Bij het vervangen D = 2 cm in de voorste formule wordt verkregen:

Gebied = 90,94 cm

Referenties

1. C. EN. NAAR. (2003). Geometrie -elementen: met oefeningen en kompasgeometrie. Universiteit van Medellin.
2. Campos, f., Cerecedo, f. J. (2014). Wiskunde 2. Patria -redactiegroep.
3. Vrijgelaten, k. (2007). Ontdek polygonen. Benchmark -onderwijsbedrijf.
4. Hendrik, V. (2013). Gegeneraliseerde polygonen. Birkhäuser.
5. Iger. (S.F.)). Wiskunde eerste semester Tacaná. Iger.
6. Jr. Geometrie. (2014). Polygonen. Lulu Press, Inc.
7. Miller, Heeren, & Hornsby. (2006). Wiskunde: redeneren en applicaties (tiende editie). Pearson Education.
8. Patiño, m. (2006). Wiskunde 5. Redactionele progreso.
9. Sada, m. Gewone 17 partijen met regel en kompas. Hersteld van: Geogebra.borg
10. Wikipedia. Heptadecágono. Hersteld van: is.Wikipedia.com