Gravicentro

Wat is de belasting?

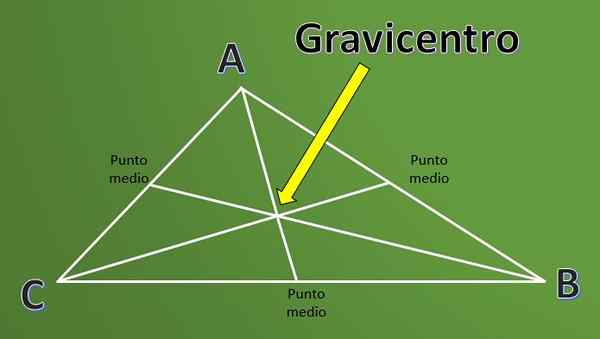
Hij Gravicentro Het is een definitie die veel wordt gebruikt in de geometrie bij het werken met driehoeken. Om de definitie van Gravicentro te begrijpen, is het eerst nodig om de definitie van "medium" van een driehoek te kennen.

De mediaan van een driehoek zijn de lijnsegmenten die bij elk hoekpunt beginnen en het middelpunt van de andere kant van deze hoekpunt bereiken.

Het snijpunt van de drie mediaan van een driehoek wordt baricentro genoemd of staat ook bekend als belastend. Het is niet voldoende om de definitie te weten, het is interessant om te weten hoe dit punt wordt berekend.

Berekening van het baricenter

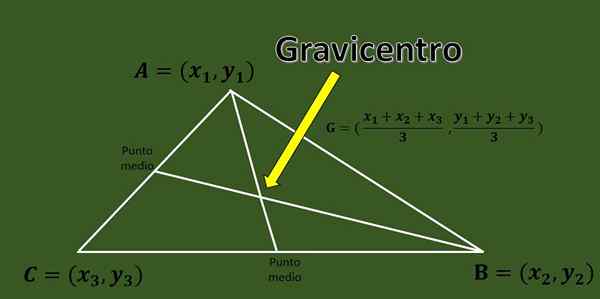
Gegeven een ABC -driehoek met hoekpunten a = (x1, y1), b = (x2, y2) en c = (x3, y3), is de gravicentro de kruising van de drie mediaan van de driehoek.

Een snelle formule die de berekening van het belasten van een driehoek mogelijk maakt, de coördinaten van zijn hoekpunten zijn is:

G = ((x1+x2+x3)/3, (y1+y2+y3)/3).

Met deze formule kunt u de locatie van de Gravicentro in het Cartesiaanse vlak kennen.

Kenmerken van de belasting

Het is niet nodig om de drie mediaan van de driehoek te traceren, want bij het tekenen van twee van hen zal deze worden aangetoond waar de belasting is.

De belastende verdeelt elke mediaan in 2 delen waarvan het aandeel 2: 1 is, dat wil zeggen, de twee segmenten van elke mediaan zijn verdeeld in segmenten van lengtes 2/3 en 1/3 van de totale lengte, de grotere afstand is de ene daar wat er zijn tussen het hoekpunt en de folder.

De volgende afbeelding illustreert deze eigenschap beter.

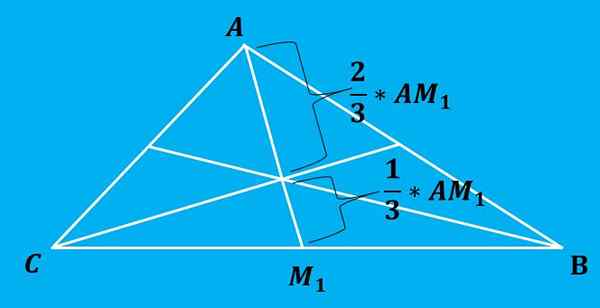
De formule voor de berekening van belastingen is heel eenvoudig toe te passen. De manier om deze formule te verkrijgen is door de rechte vergelijkingen te berekenen die elke mediaan definieert en vervolgens het snijpunt van deze lijnen te vinden.

Opdrachten

Hieronder is een kleine lijst met problemen bij de berekening van de baricenter.

1.- Gegeven een driehoek van hoekpunten a = (0.0), b = (1.0) en c = (1,1), bereken de belasting van genoemde driehoek.

Met behulp van de gegeven formule kan snel worden geconcludeerd dat de gravicentro van de ABC -driehoek is:

G = ((0+1+1)/3, (0+0+1)/3) = (2/3, 1/3).

2.- Als een driehoek hoekpunten a = (0.0), b = (1.0) en c = (1/2.1) heeft, wat zijn de coördinaten van de belastingen?

Omdat de hoekpunten van de driehoek bekend zijn, wordt de formule voor de berekening van de belasting toegepast. Daarom heeft Gravicentro coördinaten:

G = ((0+1+1/2)/3, (0+0+1)/3) = (1/2, 1/3).

3.- Bereken de mogelijke belastingbetalers voor een gelijkzijdige driehoek zodat twee van zijn hoekpunten a = (0,0) en b = (2.0) zijn.

In deze oefening worden slechts twee hoekpunten van de driehoek gespecificeerd. Om de mogelijke gravicenters te vinden, moet het derde hoekpunt van de driehoek eerst berekenen.

Aangezien de driehoek gelijkzijdig is en de afstand tussen A en B 2 is, moet de derde hoekpunt C op een afstand 2 van A en B zijn.

Met behulp van het feit dat in een gelijkzijdige driehoek de hoogte samenvalt met de mediaan en ook met behulp van de Pythagoras -stelling kan worden geconcludeerd dat de opties voor de coördinaten van het derde hoekpunt C1 = (1, √3) of C2 = (1, zijn - - - √3).

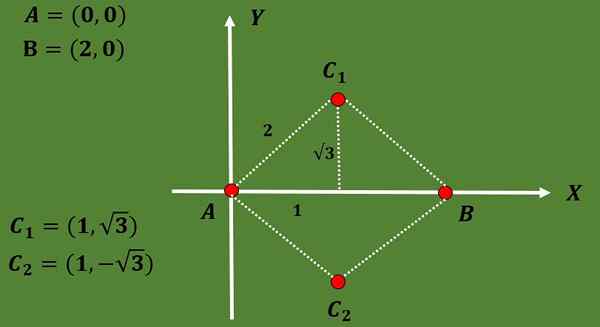
Zodat de coördinaten van de twee mogelijke gravicenters zijn:

G1 = ((0+2+1)/3, (0+0+√3)/3) = (3/3, √3/3) = (1, √3/3),

G2 = ((0+2+1)/3, (0+0 -√3)/3) = (3/3, -√3/3) = (1, -√3/3).

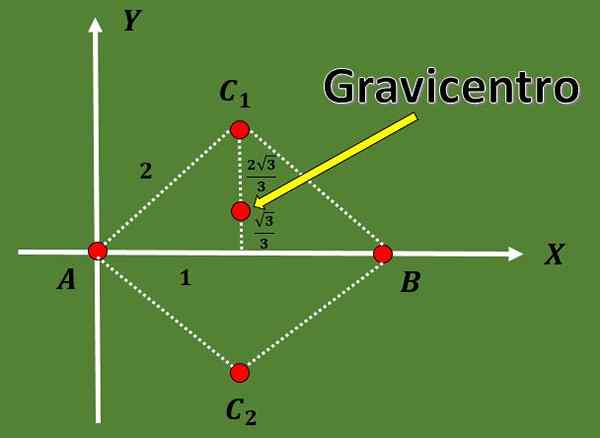
Dankzij de vorige accounts kan ook worden opgemerkt dat de mediaan is verdeeld in twee delen waarvan het aandeel 2: 1 is.