Euclidian geometrie

We leggen uit wat Euclidiaanse geometrie, de geschiedenis, elementen en we geven verschillende voorbeelden

Euclid van Alexandria en zijn elementen, door Jusepe de Ribera, naast de deur, twee niet -parallelle lijnen en een lijn die ze snijdt, ter illustratie van het vijfde postulaat. Bron: Wikimedia Commons.

Wat is Euclidian -geometrie?

De Euclidian geometrie Het is degene die wordt bestuurd door die postulaten door Euclid de Alejandría, een Griekse geometer die leefde in de richting van 300.C, ter ere van deze discipline is genoemd, omdat het de eerste was die het systematiseerde.

Deze tak van wiskunde bestudeert de eigenschappen van lijnen, vlakken, hoeken en geometrische figuren zoals polygonen, omtrek en andere conische. Vandaar dat het belang ervan in wetenschap en engineering, wiens ontwikkeling aanzienlijk heeft geleid.

Aan de andere kant was Euclidische geometrie de eerste exacte wetenschap, omdat daarmee het pad van systematisering van de wetenschap begon, evenals het gebruik van logica om aan te tonen, uit enkele axioma's, talloze stellingen genaamd theorems, om de eigenschappen te beschrijven, om de eigenschappen te beschrijven, om de eigenschappen te beschrijven van geometrische objecten.

Geschiedenis

Geometrie heeft een lange geschiedenis, omdat de interesse van de mensheid erin erg oud is en de centrale as van Euclidische geometrie het werk is Items, van de wijze Euclid van Alexandria, een stad in Egypte, en die in de vierde eeuw leefde.C.

Op het moment waren de belangrijkste eigenschappen van talloze figuren en geometrische lichamen bekend. Er was uitgebreide kennis over geometrie, maar alles was empirisch en miste systematisering.

Vervolgens heeft de koning van Egypte Ptolemaeus en de al beroemde Euclid -leraar, wiens school in Alexandrië was toevertrouwd om alle wiskundige en geometrische kennis tot nu toe te organiseren, inclusief stellingen en eigenschappen.

Euclides ging aan het werk en naast zijn discipelen schreef zijn werkelementen, die hij verdeelde in dertien boeken, als hoofdstukken. Dit werk zou een referentie worden voor geometrie voor toekomstige generaties.

Kan u van dienst zijn: opeenvolgende derivaten

Elementen van Euclid

De inhoud van de elementen is als volgt georganiseerd:

• In boeken I tot IV platte geometrie ontwikkelt zich.
• In boeken V en ik zagen de proportietheorie.
• IX -boeken zijn gewijd aan rekenkunde.
• ONTWIKKELIJKHEID VAN HET BOEK X,
• De geometrie van de ruimte in boeken xi tot xiii.

Euclidische geometrie was de basis voor veel posterieure geometrische ontwikkelingen en wordt momenteel onderwezen in alle scholen ter wereld.

Het heeft ook de deugd dat het eerste werk is om zorgvuldige demonstraties op te nemen op basis van logisch redeneren, en ook bij het geven van samenhang aan het lichaam van geometrische en wiskundige kennis van die tijd.

Basiselementen van Euclidische geometrie

Euclidische geometrie is gebouwd rond vier basiselementen, beschreven in boek I van de elementen:

1. Plek
2. Direct
3. Vlak
4. Ruimte

1. Plek

A plek Het mist afmetingen of onderdelen en onderscheidt zich van een ander punt, simpelweg door de locatie. Als twee punten A en B verschillend zijn, is het omdat ze verschillende posities hebben, die worden aangegeven via de goed bekende Cartesiaanse coördinaten (x, y) als het punt zich in het vlak bevindt, of de coördinaten (x, y, z) Als het in de ruimte is.

Het is opmerkelijk dat het Cartesiaanse systeem geen deel uitmaakt van de Items van Euclid, maar verscheen veel later in de 1600 jaar en is te wijten aan René Descartes.

2. Direct

De direct Het is een oneindige verzameling punten, en het heeft alleen lengte, niet breedte. Een deel ervan wordt meestal getekend, met pijlen in beide wijzen erop dat de lijn voor onbepaalde tijd doorgaat.

3. Vlak

A vlak Het is een onbeperkt oppervlak, dus het heeft twee dimensies en waarvan een deel wordt weergegeven, door middel van een vierkant of een rechthoek.

Daar zijn er in het vlak veel geometrische figuren, zoals lijnen, open en gesloten krommen en polygonen, onder andere.

Kan u van dienst zijn: algemene vergelijking van een lijn waarvan de helling gelijk is aan 2/3

4. Ruimte

Eindelijk is er de ruimte Met zijn drie dimensies, in staat om alle punten te huisvesten. Het bevat de vlakken en geometrische lichamen die worden gekenmerkt door hun volume, zoals polyhedra, bollen en meer.

Deze kunnen worden beschouwd als de basisdefinities van Euclidische geometrie, maar daarnaast biedt Euclides ongeveer 150 gevarieerde definities in hun werk.

Veel voorkomende ideeën

Ze bestaan ​​uit voor de hand liggende en intuïtieve feiten, die niet goed behoren tot de reikwijdte van de geometrie en worden gebruikt als concepten zich ontwikkelen. Ze verwijzen naar "dingen" in een zeer brede context:

1. Dingen hetzelfde voor iets anders, ze zijn hetzelfde met elkaar.
2. Als dingen worden toegevoegd aan een andere reeks dingen, en ze zijn allemaal hetzelfde, welke resultaten zijn ook hetzelfde.
3. Als gelijke dingen worden gestolen, is de rest ook hetzelfde.
4. Als dingen met elkaar samenvallen, is het omdat ze hetzelfde zijn.
5. Het geheel is altijd groter dan de partijen, afzonderlijk genomen.

Postulaten van Euclidische geometrie

Postulaten of axioma's zijn eenvoudige uitspraken die als waar en duidelijk worden beschouwd, dus ze vereisen geen demonstratie.

Ze vormen de basis van Euclidian en Euclid -geometrie stelt vijf in hun boek I:

1. Wees twee verschillende punten naar en B, er is slechts één lijn die erdoorheen gaat, dat wil zeggen twee punten bepalen een lijn.
2. Elk rechtlijnig segment kan voor onbepaalde tijd worden uitgebreid om een ​​lijn te vormen, daarom behoort elk segment tot een lijn.
3. Als je twee verschillende punten of A hebt, kun je altijd een cirkel trekken met midden in O en straal gelijk aan het OA -segment.
4. Alle rechte hoeken zijn congruent met elkaar.
5. Gegeven een lijn en een punt P die er niet bij hoort, is het altijd mogelijk.

Het laatste postulaat, vooral in de originele versie, ziet er niet zo eenvoudig uit als de anderen. Het zegt dat:

Kan je van dienst zijn: heptagon

“Als een rechte lijn die op twee andere lijnen valt, de twee interieurhoeken aan dezelfde zijde minder dan twee rechte hoeken maakt, zeiden rechte lijnen, wijdverbreid voor onbepaalde tijd, ze zijn (kruisen) aan de zijkant waarop de kleine hoeken zijn dat de twee rechte hoeken ".

Dat wil zeggen, oorspronkelijk postulaat 5 stelt de toestand vast zodat twee lijnen niet parallel zijn. Maar het is duidelijker wanneer het zo is geschreven dat het het tegenovergestelde illustreert, dat wil zeggen de parallellisme van de lijnen.

Voorbeelden van Euclidische geometrie

voorbeeld 1

Er zijn drie verschillende punten, gelabeld met letters A, B en C.

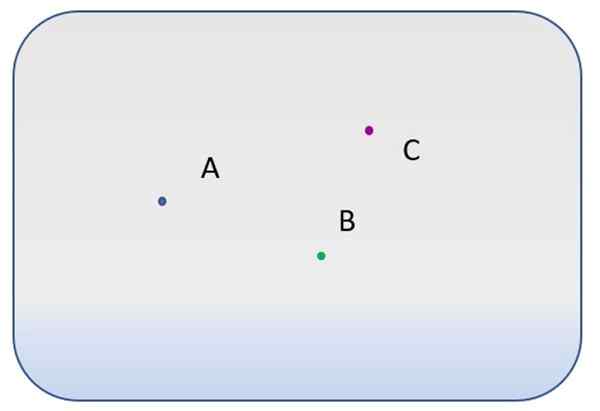
1. Hoeveel verschillende lijnen gaan door punt A?
2. En hoeveel kunnen worden getekend tussen punten A en B? En tussen a en c?
3. Is het mogelijk om een ​​lijn te trekken waarnaar punten A, B en C?

Antwoord op

Volgens postulaat I kunnen oneindige rechte lijnen worden getrokken door A, omdat twee punten nodig zijn om een ​​lijn te bepalen.

Antwoord B

Entre A en B kunnen alleen een lijn worden getrokken. En ook tussen A en C.

Antwoord C

Het is niet mogelijk dat een lijn tegelijkertijd a, b en c bevat.

Voorbeeld 2

Er wordt gevraagd om stapsgewijs een gelijkzijdige driehoek op te bouwen (alle zijden zijn gelijk), weten.

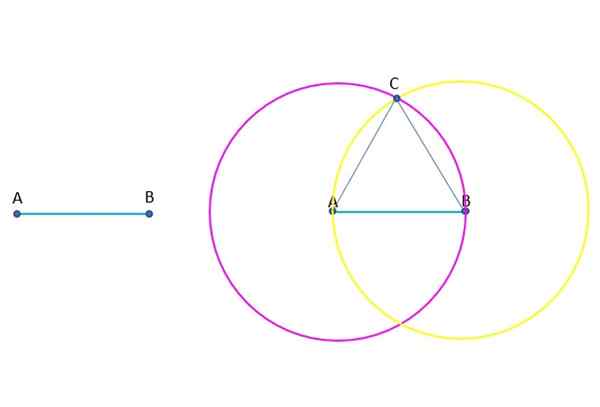Constructie van de ABC -gelijkzijdige driehoek. Bron: f. Zapata.

Antwoord

Stap 1

Een cirkel met een centrum in A en Radio AB is getekend. Dit is altijd mogelijk, volgens Postule III.

Stap 2

Een andere omtrek met het midden in B en Radio AB is getekend en de postulaat III wordt opnieuw toegepast.

Stap 3

Beide omtrek, die dezelfde straal hebben, worden gesneden op punt C. Nu kunt u segmenten tekenen die C met respectievelijk A en B verenigen, volgens Postule I.

Deze segmenten zijn radio's van de omtrek en daarom zijn de maatregelen van AC en BC gelijk aan die van AB, volgens de gemeenschappelijke notie 1. Dan is de ABC -driehoek gelijkwaardig.