Graadfuncties groter dan twee (voorbeelden)

A (polynoom) van rang groter dan twee heeft de algemene vorm:

f (x) = a₀ + naar₁x +a₂X² +.. .naar_NX^N

Met n = 3, 4, 5, ..., een niet -negatief geheel getal en de coëfficiënten_of, naar₁… naar_N, die meestal reële cijfers zijn.

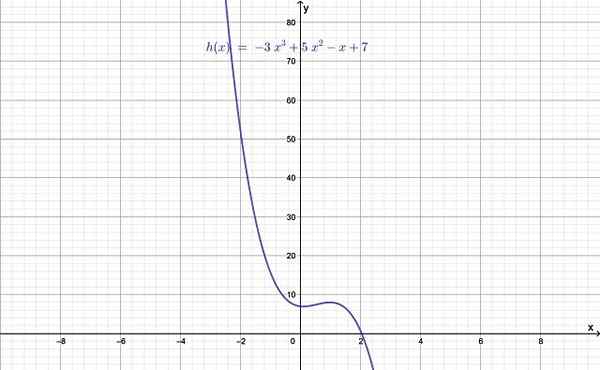Figuur 1.- Grafiek van een graadfunctie groter dan 2. Bron: f. Zapata.

De mate van de functie wordt gegeven door de waarde van N, de grootste van de exponenten en die op zijn beurt groter is dan 2. Wanneer n = 0 een constante functie is, als n = 1 is het een lineaire functie, en ten slotte met n = 2 is het een kwadratische functie.

Voorbeelden van functies van meer dan twee, in de variabele "x", zijn de volgende:

• f (x) = x³
• H (x) = - 3x³ + 5x² - X + 7
• g (x) = x⁴ - 6x² + 25

De functie f (x) = x³ Het is de eenvoudigste van alle functies van meer dan twee en de graad is 3. Een graad 3 staat ook bekend als kubieke functie. Van zijn kant is G (x) graad 4, voor 4 de maximale exponent.

De waarde van N is erg belangrijk omdat deze de algemene vorm van de grafiek bepaalt, en ook de maximale hoeveelheid wortels of kruispunten die de functie heeft met de horizontale as. Inderdaad, een functie van 3 graden zal de horizontale as op de maximaal 3 punten raken, een van de graad 4 zal het maximaal in 4 punten doen, enzovoort.

Wat betreft de onafhankelijke term, in een polynoomfunctie van elke mate geeft het de snijpunt van de functie aan met de verticale as.

Kenmerken van de polynoomfuncties van meer dan twee

Domein

Het domein van een functie is de set waarden die het mogelijk maken om de waarden van y = f (x) te berekenen. Voor polynoomfuncties is deze set die van reële n -getallen, of de set complexe getallen, indien nodig om het domein uit te breiden.

Kan u van dienst zijn: trigonometrische limieten: hoe ze op te lossen, opgeloste oefeningen

Betekent dat, gezien de polynoomfunctie f (x) = a₀ + naar₁x +a₂X² +.. .naar_NX^N, U kunt altijd elk reëel getal vervangen, de aangegeven bewerkingen uitvoeren en als gevolg daarvan een waarde van reële y = f (x) real verkrijgen.

Bereik

Het is de set gevormd door alle verkregen waarden f (x), dat wil zeggen de afbeeldingen die elke waarde van x heeft via de functie f (x). Voor polynoomfuncties groter dan 2, is deze set die van reële getallen.

Wortels van de functie

Zijn de waarden van x waarvoor wordt vervuld dat f (x) = 0. Zoals hierboven aangegeven, geeft de mate van de functie het maximale aantal wortels aan dat het kan hebben, hoewel ze niet allemaal noodzakelijkerwijs echt zijn.

Wanneer de coëfficiënten van de functie reële getallen zijn, komen de echte wortels overeen met de kruispunten van de functie met de X -as.

voorbeeld 1

De rationele wortels van de functie f (x) = 2x³ - 9x² + 7x + 6 is te vinden door de volgende stelling:

Als de wortel van f (x) = a₀ + naar₁x +a₂X² +.. .naar_NX^N Het is de B/C -vorm, dus de mogelijke waarden van B zijn factoren van een_of en de mogelijke waarden van C zijn factoren van een_N.

Voor de functie van het voorbeeld zijn de reeds vereenvoudigde combinaties: ± 6, ± 3, ± 2, ± 1, ± 3/2, ± ½. Nu wordt elk bijvoorbeeld getest via de synthetische divisieprocedure, bijvoorbeeld. Wanneer het divisieresidu 0 is, is de bewezen waarde een root:

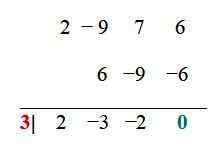
De waarde x₁ = 3 is een wortel of nul van de functie, daarom (x - 3) is een gemeenschappelijke factor van f (x), en dit kan worden geschreven als:

Het kan u van dienst zijn: Unitary Circle: Trigonometrische functies en toepassingen

f (x) = (x - 3) ∙ (2x² −3x −2)

De resterende twee wortels zijn de waarden die voldoen aan de 2x -vergelijking² −3x −2 = 0. Deze vergelijking kan worden opgelost via de algemene formule, een wetenschappelijke rekenmachine of het herhalen van het vorige Tanteo -proces.

Deze wortels zijn x₂ = 2 en x₃ = - ½, en nu f (x) kunnen worden geschreven als het product van drie factoren:

f (x) = (x - 3) ∙ (x - 2) ⋅ (x + ½)

De kruispunten van f (x) met de x -as zijn de punten: P₁ (3.0), P₂(2.0) en P₃( - ½, 0). De grafiek van de functie, verkregen met geogebra, toont zijn kruispunten met de x -as:

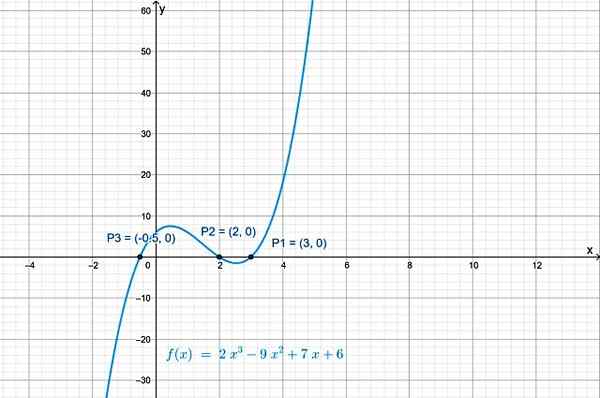Figuur 2.- Een polynoomfunctie van klasse 3 heeft drie kruispunten met de horizontale as. Bron: f. Zapata.

Kruising met de verticale as

Om de kruising van de functie met de verticale as te vinden, moet u f (0) vinden₀.

Voorbeeld 2

Zoek de kruising van f (x) = 2x³ - 9x² + 7x + 6 met de verticale as is het heel eenvoudig, bij het maken van x = 0 in f (x) wordt het verkregen:

f (x) = 6

En het snijpunt van de functie met de verticale as is p₄(0.6).

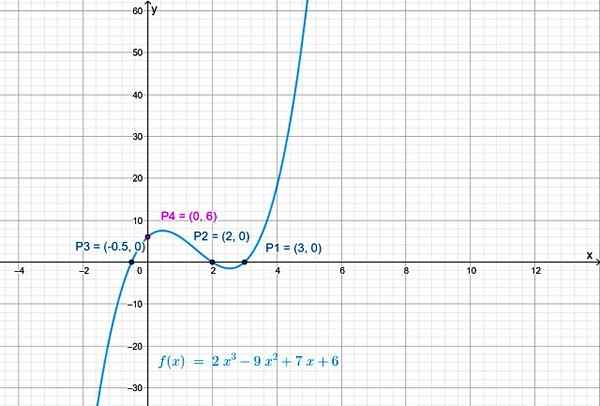figuur 3. De kruising van de curve met de verticale as maakt x = 0 in f (x). Bron: f. Zapata.

Continuïteit

Polynoomfuncties in het algemeen, en in het bijzonder die van hoger dan 2 zijn continue functies in hun hele domein, dit betekent dat ze geen sprongen, stappen, gaten of waarden hebben waarvoor ze niet zijn gedefinieerd. Ze hebben ook geen asymptoten, die verticaal, horizontaal of schuin rechtstreeks zijn waar de functie nadert zonder ze te kruisen.

Deze kwaliteiten van zachtheid en continuïteit worden gewaardeerd in de hierboven getoonde grafieken.

Grafiek van de functies van hoger dan 2

De grafieken van de functies van hogere dan 2 zijn continu en zacht, en hun vorm hangt af van de graad van de polynoom.

Kan u van dienst zijn: permutaties zonder herhaling: formules, demonstratie, oefeningen, voorbeelden

Bijvoorbeeld, die van graad 3 -ream, het heeft een negatief teken in de term met de hoogste graad).

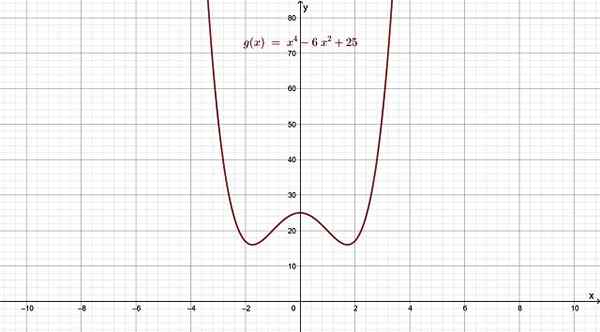Figuur 4. Polyinomische functie van graad 4, waarvan de grafiek lijkt op een letter W. Bron: f. Zapata.

Voor waarden van X weg van x = 0, zowel links als rechts, gedraagt ​​de functie hoe de term van de grootste graad zou doen, omdat dit overheerst over anderen wanneer x erg groot of erg klein wordt.

In de afbeelding die volgt de functie f (x) = 2x wordt vergeleken³ - 9x² + 7x + 6 met de functie r (x) = x³ En het wordt op prijs gesteld dat de vorm van beide curven vergelijkbaar is met waarden van X die verre van x = 0 zijn.

Voor grote X -waarden groeit de functie snel door te verzorgen tot +∞, terwijl voor negatieve X -waarden de functie snel afneemt en de neiging heeft −∞.

Figuur 5.- Alle graad N -functies gedragen zich op dezelfde manier wanneer ze weggaan van x = 0, zowel links als rechts. Bron: f. Zapata.

Het vergelijken van de koppel -grade krommen (figuur 4) met de oneven graad (figuur 2), zolang de coëfficiënt die gepaard gaat met de hoogste termijn hetzelfde teken heeft, wordt waargenomen dat de vreemde graadcurves beginnen van "y" negatief en groeien, terwijl die van doelkwaliteit in "y" positief beginnen en afnemen.

Referenties

1. Barnett, r. 20000000000000000000. Precculment: functies en afbeeldingen. 4e. Editie. McGraw Hill.
2. Berekening.DC. Polynoomfuncties. Teruggewonnen uit: berekening.DC.
3. Larson, r. 2012. Voorzetting. 8e. Editie. Cengage leren.
4. Stewart, J. 2007. Precculment: wiskunde voor berekening. 5e. Editie. Cengage leren.
5. Varsity tutorrs. Grafische polynoomfuncties. Opgehaald uit: WarsityTorm.com.