Afnemende functie hoe het te identificeren, voorbeelden, oefeningen

A afnemende functie F is een waarvan de waarde afneemt naarmate de waarde van X toeneemt. Betekent dat in een bepaald interval, rekening houdend met twee waarden x₁ en x₂ zodanig dat x₁ < x₂, Dan f (x₁)> F (x₂)).

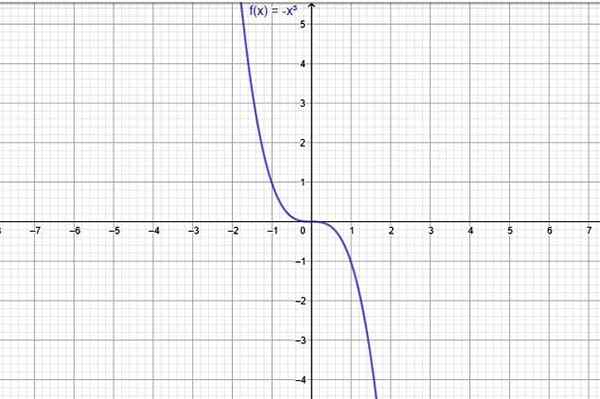
Een voorbeeld van een functie die altijd afneemt, is f (x) = -x³, wiens grafiek in de volgende figuur wordt weergegeven:

Figuur 1. Een functie die altijd afneemt in het gehele domein is f (x) = -x^3. Bron: f. Zapata door Geogebra.

Hoewel sommige functies zoals deze worden gekenmerkt door af te nemen in al hun domein, niet allemaal gedragen zich als deze, zijn er toenemende en ook die die groeien en afnemen in bepaalde domeinintervallen. De studie van groei en afname -intervallen wordt genoemd eentonigheid van de functie.

Evenzo kan de groei of afname van de functie worden overwogen op een bepaald domeinpunt. Maar elke functie die in een bepaald interval afneemt, is ook op elk punt dat erbij hoort.

[TOC]

Hoe u een afnemende functie kunt identificeren?

De functiegrafiek geeft visueel aan of deze afneemt of niet. Als, wanneer het in de toenemende betekenis van de X wordt bewogen, de functie "afdaalt", dit betekent dat deze afneemt.

En als je intervallen hebt waarin het afneemt en afwisselend groeit, wat het meest gebruikelijk is, omdat deze duidelijk worden onthuld door het gedrag van de functie gedurende zijn domein te observeren, omdat er intervallen zullen zijn waarin de functie "stijgt" en anderen in die "afdalen".

Als alternatief, als de functiegrafiek niet beschikbaar is, is het analytisch mogelijk om te bepalen of deze op een bepaald punt of in een interval afneemt, via de eerste afgeleide.

Criterium van de eerste afgeleide

Let op het gedrag van de afnemende functie die wordt getoond in figuur 2. De roze lijnsegmenten zijn rangent op de punten waarvan de coördinaten zijn [A, F (A)] En [A+H, F (A+H)] en heb een negatieve helling.

Kan u van dienst zijn: hoe wordt de informatie verkregen in een enquête?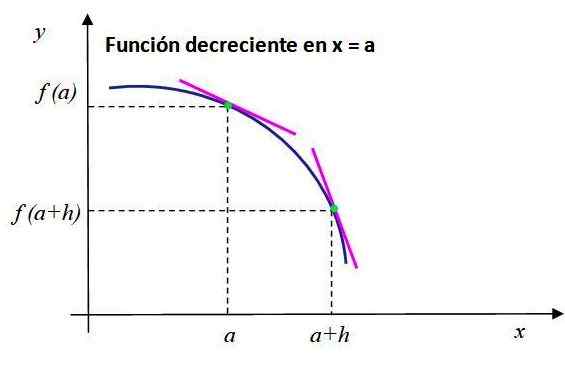Figuur 2. De helling van de raaklijn naar de grafiek van f (x) is negatief bij x = a, dan neemt de functie op dit punt af. Bron: f. Zapata.

Voor deze functie is het volgende vervuld:

F (a+h) - f (a) < 0 ⇒  F (A+H) < f (a)

Daarom kan worden gedacht dat de functie afneemt in x = a.

De eerste afgeleid van de functie f (x), geëvalueerd op x = a, die per definitie de helling is van de raaklijn naar de curve bij x = a, wordt gegeven door:

De limiet geeft aan dat de waarde van H zo klein kan worden gedaan als u wilt en suggereert dat het teken van fa), Het kan worden gebruikt om te weten of de functie op een bepaald punt afneemt, zolang het derivaat op dat moment bestaat.

Dan ja fa) < 0, Het kan worden bevestigd dat de functie afneemt en integendeel, als f '(a)> 0, Dan groeit de functie op dat moment.

Stelling voor het afnemende en groeiende functies

Eerder werd verwezen naar het gedrag van de functie op een punt. Nu kan de volgende stelling de intervallen weten waarin een functie afneemt, groeit of constant wordt:

Laat F een onderscheidbare functie zijn in het interval (a, b). Is het waar dat:

-Ja f '(x) < 0 para todo x perteneciente a (a,b), entonces f(x) es decreciente en (a,b).

-Als integendeel f '(x)> 0 voor alle x die tot (a, b) behoren, wordt gezegd dat de functie f (x) groeit in (a, b).

-Ten slotte, als f '(x) = 0 voor alle x die behoort tot het interval (a, b), is f (x) constant in genoemde interval.

Demonstratie

Stel dat f '(x) < 0 para cualquier valor de x en el intervalo (a,b), además se tienen x₁ en x₂ behorend tot het genoemde interval en de voorwaarde dat x₁< x₂.

De gemiddelde waardestelling stelt dat er een reëel getal c is, tussen x₁ en x₂, zoals dat:

Kan u van dienst zijn: gemeenschappelijke factor voor het groeperen van termen: voorbeelden, oefeningen

Zoals vastgesteld sinds x₁< x₂,  Δx is positief. Dus, omdat f '(c) negatief is, dus Δy is ook. Daarom F (x₁)) is groter dan F (x₂)) En de functie neemt effectief af op elk punt in het interval (a, b).

Stappen om te weten of een functie afneemt

Om de intervallen van afname en groei van een functie te vinden door de vorige stelling toe te passen, worden deze stappen gevolgd:

-Zoek de eerste afgeleid van de functie en match deze op nul, waardoor de resulterende vergelijking wordt opgelost. Bepaal ook de punten waarop het afgeleide niet bestaat.

Al deze punten worden genoemd kritieke punten En het is noodzakelijk om ze te vinden, omdat de derivaat in hen de mogelijkheid heeft om hun teken te veranderen, wat aangeeft dat de functie van groei naar afnemen of integendeel gaat.

-Het domein van de functie is verdeeld in intervallen bepaald door de punten waarop de eerste afgeleide wordt geannuleerd of niet bestaat.

-Ten slotte wordt het teken van het afgeleide bestudeerd op een willekeurig punt dat behoort tot elk van de intervallen verkregen in de vorige stap.

Voorbeelden van afnemende functies

De functies nemen niet allemaal met dezelfde snelheid af, sommigen doen het sneller dan andere. De volgende functies, die in de praktijk vaak verschijnen, nemen af:

De exponentiële functie

Een functie van vorm f (x) = a^X, Met een tussen 0 en 1, niet op het opnemen hiervan, neemt snel af in hun domein.

Functie 1/x

Via een online grafisch programma als een geogebra is de grafiek van de functie f (x) = 1/x gebouwd, wat bevestigt dat het afneemt in zijn hele domein.

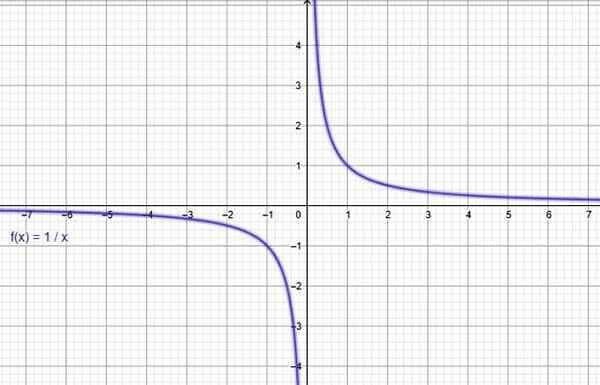figuur 3. De functie f (x) = 1/x neemt af. Bron: f. Zapata door Geogebra.

De gerelateerde functie

De functies van de vorm y = mx + b met m<0 tienen gráficas que son rectas de pendiente negativa y por lo tanto son funciones decrecientes.

Kan u van dienst zijn: wiskundige gelijkheid

Oefening opgelost

Zoek eventueel de afname -intervallen van de functie:

f (x) = x⁴ - 6x² - 4

Oplossing

De eerste stap is om te vinden f '(x):

f '(x) = 4x³ - 12x

De eerste afgeleide van F (x) is een continue functie, dat wil zeggen dat het geen discontinuïteitspunten heeft, maar wordt geannuleerd in:

4x³ - 12x = 0 = 4x (x²-3) = 0

De oplossingen van deze vergelijking zijn: x₁ = 0, x₂ = - √3 en x₃ = √3. Dit zijn de kritieke punten, die het domein van f (x) in de intervallen verdelen: (-∞,- √3); (- √3.0); (0, √3); (√3, ∞+).

Vervolgens wordt de eerste afgeleid in een willekeurige X -waarde geëvalueerd, die tot elk interval behoort. Deze waarden werden gekozen:

Voor (-∞,- √3)

F '(-2) = 4 (-2)³ - 12x (-2) = -32+24 = -8

Voor (- √3.0)

F '(-1) = 4 (-1)³ - 12x (-1) = -4+12 = 8

Voor (0, √3)

f '(1) = 4 (1)³ - 12x (1) = 4-12 = -8

Voor (√3, ∞+)

f '(2) = 4 (2)³ - 12x (2) = 32-24 = 8

Net als verschillende intervallen, is het een goed idee om een ​​tafel te maken om de resultaten te organiseren. De opwaartse pijl geeft aan dat de functie groeit en omlaag, wat afneemt:

Er wordt geconcludeerd dat de functie afneemt met de intervallen (-∞,- √3) en (0, √3) en groeit in de resterende intervallen. De oorspronkelijke functie in Geogebra kan eenvoudig worden gecontroleerd door graferen.

Referenties

1. Ayres, f. 20000000000000000000. Berekening. 5ed. MC Graw Hill.
2. Leithold, l. 1992. Berekening met analytische geometrie. Harla, s.NAAR.
3. Purcell, E. J., Varberg, D., & Rigdon, s. EN. (2007). Berekening. Mexico: Pearson Education.
4. Matemobile. Functies, groeien, afnemen en constant. Hersteld van: Matemovil.com
5. Stewart, J. 2006. Precculment: wiskunde voor berekening. 5e. Editie. Cengage leren.