Constante kenmerken functie, voorbeelden, oefeningen

De constante functie Het is er een waarin de waarde van en. Met andere woorden: een constante functie heeft altijd de vorm  f (x) = k, waar k Het is een echt nummer.

Door de constante functie in het coördinatensysteem te graferen XY, Het is altijd een rechte lijn parallel aan de horizontale as of as van de X.

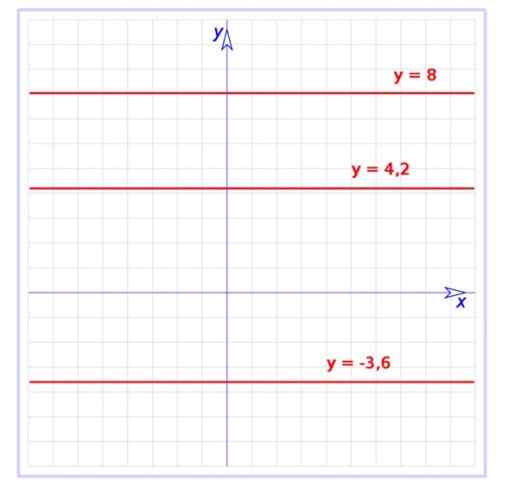
Figuur 1. Grafiek van verschillende constante functies op het Cartesiaanse vlak. Bron: Wikimedia Commons. Gebruiker: Hite [Public Domain]

Deze functie is een bepaald geval van de Gerelateerde functie, wiens grafiek ook een rechte lijn is, maar met helling. De constante functie heeft een nul in behandeling, dat wil zeggen, het is een horizontale lijn, zoals te zien in figuur 1.

Er is de grafiek van drie constante functies:

f (x) = -3.6

G (x) = 4.2

H (x) = 8

Ze zijn allemaal recht parallel aan de horizontale as, de eerste bevindt zich onder die as, terwijl de resterende.

[TOC]

Kenmerken van de constante functie

We kunnen de belangrijkste kenmerken van de constante functie als volgt samenvatten:

-De grafiek is een horizontale rechte lijn.

-Het heeft een unieke kruising met de as En, waard k.

-Het is continu.

-De beheersing van de constante functie (de set waarden die de X) is de reeks reële getallen R.

-De route, het bereik of de tegenspraak (de set waarden die de variabele neemt En) is gewoon de constante k.

Voorbeelden

De functies zijn nodig om verbanden te leggen tussen grootten die op een of andere manier van elkaar afhankelijk zijn. De bestaande relatie tussen hen kan wiskundig worden gemodelleerd, om te weten hoe een van hen zich gedraagt ​​wanneer de andere varieert.

Kan u van dienst zijn: papomudas

Dit helpt bij het bouwen van modellen voor veel situaties en voorspellingen doen over hun gedrag en evolutie.

Ondanks de schijnbare eenvoud heeft de constante functie veel toepassingen. Bijvoorbeeld als het gaat om het bestuderen van magnitudes die in de tijd constant blijven, of op zijn minst, voor een aanzienlijke tijdstip.

Op deze manier gedragen magnitudes zich in situaties zoals de volgende:

-De snelheid Cruise van een auto die op een lange rechtlijnige snelweg beweegt. Zolang het niet stopt of versnelt, heeft de auto een uniforme rechtlijnige beweging.

Figuur 2. Als de auto niet stopt of versnelt, heeft deze een uniforme rechtlijnige beweging. Bron: Pixabay.

-Een volledig geladen en losgekoppelde condensor uit een circuit, heeft een last constant in de tijd.

-Ten slotte, een vaste tarief parkeren, onderhoudt een prijs constant, ongeacht hoe lang een auto daar parkeerde.

Een andere manier om een ​​constante functie weer te geven

De constante functie kan afwisselend als volgt worden weergegeven:

f (x) = kx⁰

Sinds elke waarde van X Terug verhoogd tot 0 geeft 1 als gevolg daarvan, de vorige uitdrukking wordt gereduceerd tot het bekende:

f (x) = k

Dat gebeurt natuurlijk zolang de waarde van k is anders dan 0.

Daarom wordt de constante functie ook geclassificeerd als een polynoomfunctie graad 0, omdat de exponent van de variabele X Het is 0.

Opgeloste oefeningen

- Oefening 1

Beantwoord de volgende vragen:

a) kan worden bevestigd dat de regel gegeven door x = 4 een constante functie is? Reden uw antwoord.

B) Kan een constante functie kruising hebben met de X -as?

c) is de functie f (x) = w constant²?

Antwoord op

Hier is de grafiek van de lijn x = 4:

Kan u van dienst zijn: statistische variabelen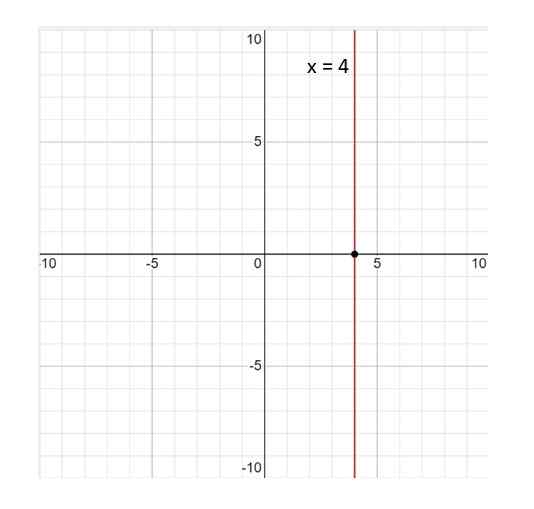 figuur 3. Grafiek van de lijn x = 4. Bron: f. Zapata.

De lijn x = 4 is geen functie; Per definitie is een functie een relatie zodanig dat tot elke waarde van de variabele X Het komt overeen met een enkele waarde van En. En in dit geval wordt dit niet vervuld, omdat de waarde x = 4 wordt geassocieerd met oneindige waarden van En. Daarom is het antwoord nee.

Antwoord B

Over het algemeen heeft een constante functie geen kruising met de as X, Tenzij het is y = 0, in welk geval het de as is X Goed gezegd.

Antwoord C

Ja, sinds W Het is constant, het vierkant is ook. Wat interesses is dat W Het hangt niet af van de invoervariabele X.

- Oefening 2

Zoek de kruising tussen de functies f (x) = 5 En G (x) = 5x - 2

Oplossing

Om de kruising tussen deze twee functies te vinden, kunnen ze respectievelijk worden herschreven als:

y = 5; y = 5x - 2

Ze zijn afgestemd, verkrijgen:

5x - 2 = 5

Dat is een lineaire vergelijking in de eerste graad, waarvan de oplossing is:

5x = 5+2 = 7

x = 7/5

Het snijpunt is (7/5; 5).

- Oefening 3

Toon aan dat degene die is afgeleid van een constante functie 0 is.

Oplossing

Uit de definitie van derivaat hebt u:

 f (x) = k

f (x+h) = k

De definitie vervangen:

Het bovenstaande is zinvol, omdat de afgeleide van een functie wordt gedefinieerd als de helling van de lijn die op een bepaald punt op de curve raakt. De constante functie heeft een nul in behandeling en elke raaklijn er ook aan.

Als we bovendien aan de afgeleide denken als een wisselkoers Dy/dx, De constante functie ervaart geen enkele verandering, daarom is de afgeleide ervan nietig.

Kan u van dienst zijn: multiplicatief principe: teltechnieken en voorbeelden

- Oefening 4

Vind de onbepaalde integraal van f (x) = k.

Oplossing

- Oefening 5

Een mobiele telefoonbedrijf biedt onbeperkte internetservice met een vast tarief dat $ 15 per maand betaalt. Wat is de prijsfunctie volgens de tijd?

Oplossing

Laat P de prijs zijn die moet worden betaald voor $ en T -tijd, die in dagen kan worden uitgedrukt. De functie is als volgt vastgesteld:

P (t) = 15

- Oefening 6

De volgende versus tijdgrafiek komt overeen met de beweging van een deeltje.

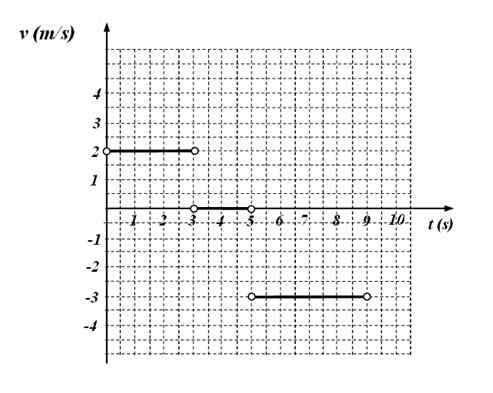Figuur 4. Functie v (t) functiegrafiek voor oefening 6. Bron: f. Zapata.

Het wordt gevraagd:

a) Schrijf een uitdrukking voor snelheidsfunctie als een functie van de tijd V (t).

b) Vind de afstand die door de mobiel wordt afgelegd in het tijdsinterval tussen 0 en 9 seconden.

Oplossing voor

Van de grafiek die laat zien dat:

-V = 2 m/s In het tijdsinterval tussen 0 en 3 seconden

-De mobiel wordt tussen 3 en 5 seconden vastgehouden, omdat de snelheid in dit interval 0 waard is.

-V = - 3 m/s Tussen 5 en 9 seconden.

Het is een voorbeeld van een stuk stukken of functie in delen, die op zijn beurt zijn samengesteld uit constante functies, alleen geldig voor de aangegeven tijdsintervallen. Er wordt geconcludeerd dat de gezochte functie is:

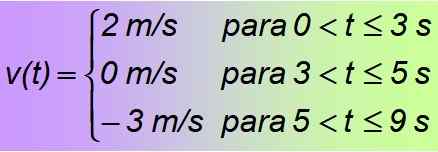
Oplossing B

Vanaf grafiek V (t) kan de afstand die door de mobiel wordt afgelegd, worden berekend, die numeriek gelijk is aan het gebied laag/op de curve. Op deze manier:

-Afstand afgelegd tussen 0 en 3 seconden = 2 m/s . 3 s = 6 m

-Tussen 3 en 5 seconden werd hij vastgehouden, daarom reed hij geen afstand.

-Afstand afgelegd tussen 5 en 9 seconden = 3 m/s . 4 s = 12 m

In totaal tourde de mobiel 18 m. Zie dat hoewel de snelheid negatief is in het interval tussen 5 en 9 seconden, de afgelegde afstand positief is. Wat er gebeurt, is dat de mobiel in die tijdsinterval de betekenis van zijn snelheid had veranderd.

Referenties

1. Geogebra. Constante functies. Hersteld van: Geogebra.borg.
2. Maplesoft. De constante functie. Hersteld van: Maplesoft.com.
3. Wikilibros. Berekening in een variabele/functies/constante functie. Hersteld van: is.Wikibooks.borg.
4. Wikipedia. Constante functie. Opgehaald uit: in.Wikipedia.borg
5. Wikipedia. Constante functie. Hersteld van: is.Wikipedia.borg.