Bijectieve functie Wat is, hoe wordt het gedaan, voorbeelden, oefeningen
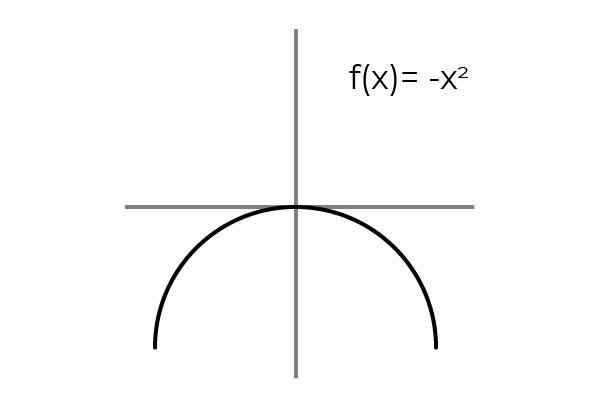
- 4526
- 593
- Dr. Rickey Hudson
A Bijectieve functie Het is er een die voldoet aan de dubbele staat van zijn Injectief en overjectief. Dat wil zeggen, alle elementen van het domein hebben een enkele afbeelding in het codominium, en op zijn beurt is het codominium gelijk aan het bereik van de functie ( RF )).
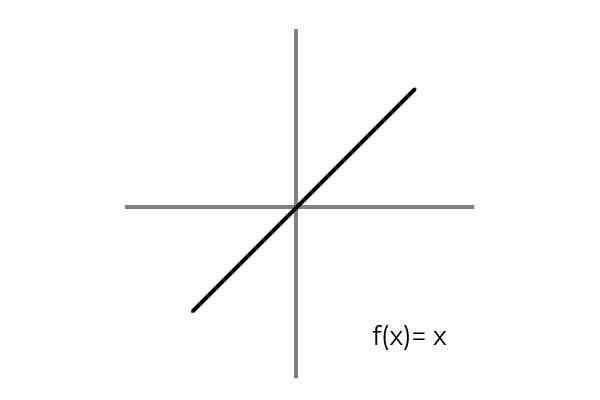
Het wordt vervuld wanneer een biunivocale relatie tussen de elementen van domein en codominium wordt overwogen. Een eenvoudig voorbeeld is de functie F: R → R gedefinieerd door de lijn F (x) = x
 Bron: auteur
Bron: auteur Opgemerkt wordt dat voor elke waarde van het domein of de set vertrek (beide termen gelijkelijk toepassen) er een enkele afbeelding is in het codominium- of aankomstset. Bovendien is er geen element van codominium dat geen beeld is.
Dus F: R → R gedefinieerd door de lijn F (x) = x is bijectief
[TOC]
Hoe is een bijjectieve functie?
Om hierop te reageren, is het noodzakelijk om duidelijke concepten te hebben die verband houden met Injectiviteit En Overjectiviteit van een functie, Naast de criteria voor conditioneringsfuncties om ze aan te passen aan de vereisten.
Injectiviteit van een functie
Een functie is Injectief Wanneer elk van de elementen van het domein gerelateerd is aan een enkel element van codominium. Een element van codominium kan slechts een beeld zijn van een enkel element van het domein, op deze manier kunnen de waarden van de afhankelijke variabele niet worden herhaald.
Overwegen Injectief Het volgende moet worden vervuld tot een functie:
∀ x1 ≠ x2 ⇒ F (x1 ) ≠ f (x2 ))
Overjectiviteit van een functie
Een functie is geclassificeerd als Overtuigen, Als elk element van het codominium een beeld is van ten minste één domeinelement.
Overwegen Overtuigen Het volgende moet worden vervuld tot een functie:
Kan u van dienst zijn: vervangende bemonsteringZijn F: DF → CF
∀ B ℮ CF EN naar ℮ DF / F (a) = b
Dit is de algebraïsche manier om dat vast te stellen voor elke "B" die tot C behoortF Er is een "A" die bij D hoortF zodanig dat de functie geëvalueerd in "A" gelijk is aan "B".
Conditionering van functies
Soms een functie die niet is Bijectief, kan bepaalde conditionering ondergaan. Deze nieuwe voorwaarden kunnen er een van een Bijectieve functie. Alle soorten wijzigingen in het domein en het codominium van de functie zijn geldig, waarbij het doel is om te voldoen aan de injectiviteit en de eigenschappen over -Alcheivity in de overeenkomstige relatie.
Voorbeelden: opgeloste oefeningen
Oefening 1
Wees de functie F: R → R gedefinieerd door de lijn F (x) = 5x +1
A: [Alle reële getallen]
Opgemerkt wordt dat er voor elke domeinwaarde een afbeelding in het codominium is. Deze afbeelding is uniek, wat maakt F er een zijn Injectieffunctie. Op dezelfde manier zien we dat het codominium van de functie gelijk is aan het bereik. Aldus de toestand van de toestand van Overtolligheid.
Injectief zijn en tegelijkertijd overtuigend zijn, kunnen we dat concluderen
F: R → R gedefinieerd door de lijn F (x) = 5x +1 is een Bijectieve functie.
Dit is van toepassing op alle lineaire functies (functies waarvan de grotere mate van de variabele één is).
Oefening 2
Wees de functie F: R → R gedefinieerd door F (x) = 3x2 - 2
Bij het trekken van een horizontale lijn wordt opgemerkt dat de grafiek meer dan eens wordt gevonden. Daarom de functie F Het is niet injectief en daarom zal het dat niet zijn Bijectief Terwijl ze worden gedefinieerd in R → R
Op dezelfde manier zijn er codominiumwaarden die geen afbeeldingen zijn van een domeinelement. Hierdoor is de functie niet overjectief, die ook verdient om de aankomstset te conditioneren.
Kan u van dienst zijn: theorie instellen: kenmerken, elementen, voorbeelden, oefeningenHet domein en het codominium van de functie zijn geconditioneerd
F: [0 , ∞] → [ - 2 , ∞ ]
Waar wordt opgemerkt dat het nieuwe domein waarden van nul tot positieve oneindigheid bestrijkt. Het vermijden van de herhaling van waarden die de injectiviteit beïnvloeden.
Aldus is het codominium gemodificeerd, geteld van "-2" naar de positieve oneindigheid, waardoor het codominium de waarden die niet overeenkwamen met een domeinelement elimineren
Op deze manier kan ervoor worden gezorgd dat F : [0 , ∞] → [ - 2 , ∞ ] gedefinieerd door F (x) = 3x2 - 2
Het is bijectief
Oefening 3
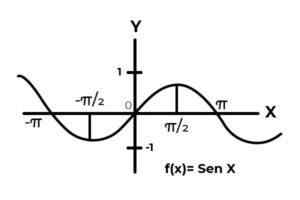
Wees de functie F: R → R gedefinieerd door F (x) = sin (x)
In de interval [[ -∞ , +∞ ] De sinusfunctie varieert de resultaten tussen nul en één.
 Bron: auteur.
Bron: auteur. De functie F Het komt niet overeen met de criteria voor injectiviteit en overjectiviteit, omdat de afhankelijke variabele waarden elk π -interval worden herhaald. Bovendien de voorwaarden van het codominium buiten de interval [ -elf ] Ze zijn geen beeld van een domeinelement.
Bij het bestuderen van de functieafbeeldingen F (x) = sin (x) intervallen worden waargenomen wanneer het gedrag van de curve voldoet aan de criteria van Bijectiviteit. Zoals het interval DF = [[ π/2,3π/2 ] Voor domein. EN CF = [-1, 1] Voor codominium.
Waarbij de functie de resultaten varieert van 1 tot -1, zonder enige waarde in de afhankelijke variabele te herhalen. En tegelijkertijd is het co -oominium gelijk aan de waarden die door de uitdrukking worden aangenomen Sin (x)
Op deze manier de functie F: [ π/2,3π/2 ] → [-1, 1] gedefinieerd door F (x) = sin (x). Het is bijectief
Oefening 4
Verhoog de nodige voorwaarden voor DF en CF. Zodat de uitdrukking
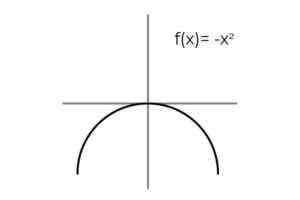
Kan u van dienst zijn: bemonsteringsfout: formules en vergelijkingen, berekening, voorbeeldenF (x) = -x2 Bijding zijn.
 Bron: auteur
Bron: auteur De herhaling van de resultaten wordt waargenomen wanneer de variabele tegengestelde waarden inhoudt:
F (2) = f (-2) = -4
F (3) = f (-3) = -9
F (4) = f (-4) = -16
Het domein is geconditioneerd en beperkt het tot de rechterkant van de echte lijn.
DF = [0 , +∞ ]
Op dezelfde manier wordt opgemerkt dat het bereik van deze functie het interval is [[ -∞ , 0], die, door te dienen als codominium, voldoet aan de voorwaarden van overjectiviteit.
Op deze manier kunnen we dat concluderen
De uitdrukking F: [0 , +∞ ] → [ -∞ , 0] gedefinieerd door F (x) = -x2 Het is bijectief
Voorgestelde oefeningen
Controleer of de volgende functies bijectief zijn:
F: [0 , ∞) → R gedefinieerd door F (x) = 3 (x + 1)2 +2
F: [ 3π/2,5π/2 ] → R gedefinieerd door F (x) = 5ctg (x)
F: [ -π,π ] → R gedefinieerd door F (x) = cos (x - 3)
F: R → R gedefinieerd door de lijn F (x) = -5x + 4
Referenties
- Inleiding tot logica en kritisch denken. Merrilee h. Zalm. Universiteit van Pittsburgh
- Problemen in wiskundige analyse. Piotr Barar, Alfred Witkowski. Universiteit van Wroclaw. Pool.
- Elementen van abstracte analyse. Mícheál O'Searcoid PhD. Afdeling Wiskunde. University College Dublin, Beldfield, Dublind 4
- Inleiding tot logica en de methodologie van de deductieve wetenschappen. Alfred Tarski, New York Oxford. Oxford Universiteit krant.
- Wiskundige analyseprincipes. Enrique Linés Escardó. Redactionele terugvordering. Tot 1991. Barcelona, Spanje.
- « Glycogeenstructuur, synthese, afbraak, functies
- Karakteristieke enzymenkenmerken, actiemechanismen, voorbeelden »

