Dynamische of kinetische wrijvingscoëfficiënt, voorbeelden, oefeningen

De Dynamische wrijving of kinetisch Het is degene die plaatsvindt tussen twee lichamen in contact wanneer het oppervlak van een van hen beweegt ten opzichte van het oppervlak van de andere. In een doos die de wrijving op een helling schuift, is bijvoorbeeld dynamisch en verdeeld op het contactoppervlak van het blok.

De helling moet groot genoeg zijn, zodat de tangentiële component van het gewicht gelijk is aan of overwint de wrijvingskracht, anders zou het blok dat afdaalt zou stoppen.

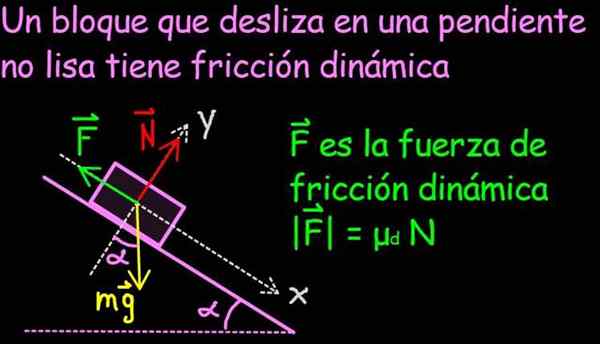Figuur 1. De wrijvingskracht wordt verdeeld op het contactoppervlak van het blok, maar in het krachtenschema wordt het weergegeven als een enkele kracht f, bron: f. Zapata

De wrijvingskracht is van extreem belang in het dagelijks leven, omdat het de voortbeweging van mensen, dieren en voertuigen mogelijk maakt. Op een wrijvingsloos oppervlak, zoals dat van een ijs, is het niet mogelijk om de beweging te starten.

Wrijving stelt onze auto's ook in staat om te stoppen zodra ze in beweging zijn.

Bij het aanbrengen van de remmen worden remblokken vastgemaakt tegen wielschijven en dankzij dynamische wrijving stoppen de rotatie ervan. Maar het is niet voldoende om goede remmen te hebben, het is noodzakelijk dat er voldoende wrijvingssterkte is tussen de banden en de vloer, omdat dit uiteindelijk de kracht is waarvan we afhankelijk zijn, zodat de auto stopt.

De mensheid heeft geleerd om wrijving af te handelen vanwege zijn voordeel. Zo begon met het gebruik van wrijving tussen twee stukken droog hout om vuur te maken.

De natuur heeft ook geleerd om wrijving in zijn voordeel aan te pakken. De synoviale membranen die de botten van de gewrichten bedekken, zijn bijvoorbeeld een van de oppervlakken met de laagste wrijvingscoëfficiënt die bestaat.

[TOC]

Dynamische wrijvingscoëfficiënt

De eerste die systematisch de beweging van een blok bestudeerde dat op een plat oppervlak glijdt, was Leonardo da Vinci, maar zijn studies bleven onopgemerkt.

Kan u van dienst zijn: Dirac Jordan Atomic Model: kenmerken en postulaten

Pas in de zeventiende eeuw herontdekte de Franse natuurkundige Guillaume Amontons de wrijvingswetten:

Dynamische wrijvingswetten

1.- De wrijvingskracht aanwezig in een blok dat op een plat oppervlak glijdt, verzet zich altijd tegen de richting van de beweging.

2.- De grootte van de dynamische wrijvingskracht is evenredig met de normale strakheid of kracht tussen de oppervlakken van het blok en het ondersteuningsvlak.

3.- De proportionele constante is de wrijvingscoëfficiënt, statisch μ_En In het geval van geen slip en dynamische μ_D Als er is. De wrijvingscoëfficiënt is afhankelijk van de materialen van de oppervlakken in contact en de toestand van ruwheid.

4.- De wrijvingskracht is onafhankelijk van het schijnbare contactgebied.

5.- Zodra de beweging van het ene oppervlak begint met betrekking tot het andere, is de wrijvingskracht constant en hangt hij niet af van de relatieve snelheid tussen de oppervlakken.

In het geval is er geen glijdende, statische wrijving toegepast waarvan de kracht kleiner is dan of gelijk is aan de statische wrijvingscoëfficiënt vermenigvuldigd door normaal.

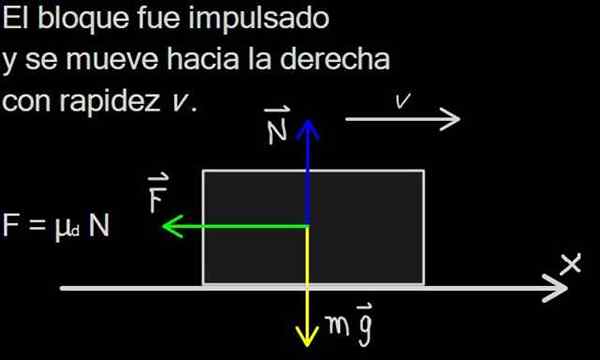
Figuur 2. De dynamische wrijvingskracht verzet zich tegen de bewegingsrichting en de omvang ervan is evenredig met die van normale kracht. De evenredigheidsconstante is de dynamische wrijvingscoëfficiënt. Bron: f. Zapata.

Het laatste onroerend goed was het resultaat van de bijdrage van de Franse natuurkundige Charles Augustin van Coulomb, beter bekend om zijn beroemde krachtwet tussen specifieke elektrische ladingen.

Deze waarnemingen leiden ons naar het wiskundige model voor dynamische wrijvingskracht F:

F = μ_D N

Waar μ_D Het is de dynamische wrijvingscoëfficiënt en N is de normale kracht.

Hoe u de dynamische wrijvingscoëfficiënt kunt bepalen?

De dynamische wrijvingscoëfficiënt tussen twee oppervlakken wordt experimenteel bepaald. De waarde ervan hangt niet alleen af ​​van de materialen op beide oppervlakken, maar van de staat van ruwheid of polijsten die ze hebben, evenals de netheid ervan.

Kan u van dienst zijn: mechanische golven: kenmerken, eigenschappen, formules, typen

Een manier om het te bepalen is om een ​​bekende doos op een horizontaal oppervlak te stimuleren en te schuiven.

Als de snelheid bekend is op het moment van gedreven en de afgelegde afstand van die tijd wordt gemeten, is het mogelijk om de remversnelling te kennen als gevolg van dynamische wrijving.

Experiment 

In dit experiment wordt de initiële snelheid gemeten v en de afstand D, Dus de remversnelling is:

A = - V² / 2d

Het krachtenschema wordt getoond in figuur 2. De grootte van het gewicht is de massa M van het blok vermenigvuldigd door de versnelling van de zwaartekracht G, en zoals bekend, wijst het gewicht altijd verticaal naar beneden.

N Het is de normale kracht als gevolg van de stuwkracht van het ondersteuningsoppervlak en is altijd loodrecht (of normaal) naar het vlak. Er bestaat normaal terwijl de oppervlakken in contact zijn en stoppen zodra de oppervlakken zijn gescheiden.

De kracht F vertegenwoordigt de dynamische wrijvingskracht. Het is eigenlijk verdeeld op het onderoppervlak van het blok, maar we kunnen het vertegenwoordigen als een enkele kracht F toegepast in het midden van het blok.

Omdat er verticale balans is, is de omvang van het normaal N Het is gelijk aan die van het gewicht mg:

N = mg

In de horizontale richting produceert de wrijvingskracht de vertraging van het massablok M volgens de tweede wet van Newton:

-F = m a

De wrijvingskracht F wijst naar links, dus de horizontale component is negatief, m is de massa van het blok en A is de remversnelling.

Had eerder verkregen A = - V² / 2d En ook het dynamische wrijvingsmodel geeft aan dat:

F = μd n

Vervangen in de vorige vergelijking die u hebt:

-μ_D N = - v² / 2d

Rekening houdend met dat n = mg, kunt u de dynamische wrijvingscoëfficiënt al wissen: 

Kan u van dienst zijn: Schrödinger Atomic Model

μ_D = v² / (2d mg)

Rocy -coëfficiënttabel van sommige materialen

De volgende tabel toont de statische en dynamische wrijvingscoëfficiënten voor verschillende materialen. Opgemerkt moet worden dat systematisch de statische wrijvingscoëfficiënt altijd groter is dan de dynamische wrijvingscoëfficiënt.

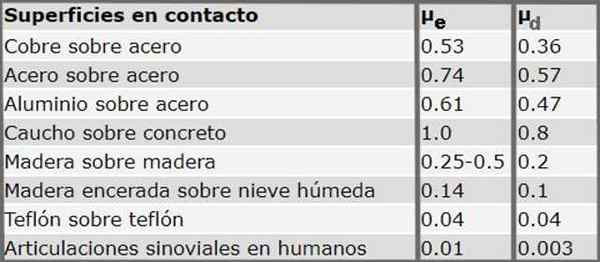figuur 3. Statische en dynamische wrijvingscoëfficiënten voor verschillende oppervlakken in contact. Bron: Serway R.NAAR. Fysiek. McGraw-Hill (1992)

Opdrachten

- Oefening 1

Een blok van 2 kg deeg op een horizontale vloer wordt gepromoot en het wordt vrijgegeven. Op het moment van vrijgegeven wordt een snelheid van 1,5 m/s opgenomen. Vanaf dat moment tot het blok stopt met dynamische wrijving 3 m. Bepaal de kinetische wrijvingscoëfficiënt.

Oplossing

Volgens de formule verkregen in het voorbeeld van de vorige sectie is het dynamische (of kinetische) coëfficiënt:

μ_D = v² / (2d mg) = 1.52 / (2x3x2 x9.8) = 0,019.

- Oefening 2

Wetende dat het blok in figuur 1 daalt met constante snelheid, dat de massa van het blok 1 kg is en dat de helling van het vlak 30º is, bepaalt:

a) de waarde van de dynamische wrijving

b) De dynamische wrijvingscoëfficiënt tussen het blok en het vlak.

Oplossing

In figuur 4 wordt de bewegingsvergelijking (tweede wet van Newton) getoond voor het probleem van een blok dat een helling afdaalt met wrijvingscoëfficiënt μ_D  en α -helling (zie krachtenschema in figuur 1)

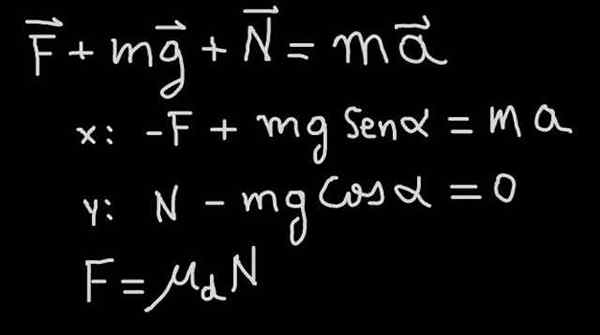Figuur 4. De tweede wet van Newton was van toepassing op het blok dat op een helling glijdt met wrijving. Bron: f. Zapata.

In onze oefening wordt ons verteld dat het blok daalt met constante snelheid, daarom daalt af met versnelling A = 0. Van daaruit volgt dat de wrijvingskracht zodanig is dat deze gelijk is aan de tangentiële component van het gewicht: f = mg sen (α).

In ons geval M = 1 kg en α = 30º zodat de wrijvingskracht f een waarde van 4,9n heeft.

Aan de andere kant is de normale kracht N hetzelfde en in tegenstelling tot de loodrechte component van het gewicht: n = mg cos (α) = 8.48n .

Van daaruit volgt dat de dynamische wrijvingscoëfficiënt is:

μ_D = F / n = 4,9n / 8.48n = 0,57

Referenties

1. Alonso m., Fin e. 19700000000000. Fysiek. Deel I. Mechanica. Inter -American Educational Fund s.NAAR.
2. Bauer, W. 2011. Fysica voor engineering en wetenschappen. Deel 1. MC Graw Hill.
3. Hewitt, p. 2012. Conceptuele fysieke wetenschap. VIJFDE EDITIE.
4. Rex, a. 2011. Fundamentals of Physics. Pearson. 
5. Serway r. 1992. Fysiek. McGraw-Hill.
6. Jong, h. 2015. Universitaire natuurkunde met moderne natuurkunde. 14e ed. Pearson.