Verpakkingsfactor

De verpakkingsfactor is een fractie die aangeeft hoeveel volume de deeltjes bezetten, of atomen, ionen of moleculen, in de interne ruimte van een kristal. De waarde ervan is altijd minder dan 1, wat 100% van het volume van het glas wordt; Meer precies, de eenheidscel, die de kleinste weergave is van het hele glas.

Een 100% verpakkingsfactor betekent dat de deeltjes het volume van de unitaire cel in zijn geheel bezetten. Fysiek is het onmogelijk om dit te laten gebeuren, omdat het bijvoorbeeld zou impliceren dat de atomen hun radio's vervormen en oplossen alsof ze een "elektronische vloeistof" zijn. De geometrie van atomen, bolvormig voor gemak, resulteert altijd in lege ruimtes tijdens de verpakking.

In zoete machines in zoete verstreken vertelt de verpakkingsfactor ons hoe "strak" de deeltjes van een kristal zijn: hoe groter het is, hoe meer tandvlees, of atomen, er zal in de ruimte zijn

In de definitie van de verpakkingsfactor wordt aangenomen dat de atomen bestaan ​​uit stijve sferen, zoals tandvlees of snoepballen van een afgegeven machine (superieure afbeelding). Onder de bollen zullen er altijd holle ruimtes zijn waar kleinere bollen (onzuiverheden of additieven kunnen worden gesluierd).

Als we de verpakkingsfactor verhogen, worden de bollen geperst, waardoor het meest compacte en dichte glas wordt; of aan de andere kant, meer vervormbaar, zoals bij kneedbare en ductiele metalen.

De verpakkingsfactor is van toepassing op elk type glas. De berekening ervan kan echter een beetje vervelend worden, dus het zal alleen worden overwogen voor atomaire kristallen met eenvoudige structuren.

[TOC]

Verpakkingsfactorformule

De verpakkingsfactor wordt meestal uitgedrukt als percentages. Als de waarde bijvoorbeeld 40% is, betekent dit dat de deeltjes nauwelijks 40% van de totale ruimte van de eenheidscel innemen; of wat hetzelfde is als dat 60% van het glas "leeg" is.

Het bovenstaande verduidelijkt wat de formule is voor het berekenen van deze factor:

• Ugly = (volume atomen)/ (eenheidscelvolume)

Waar lelijk betekent Atomaire pakkingsfactor, Wat zijn de eenvoudigste kristallen.

Het volume van de eenheidscel hangt af van zijn parameters (zoals de lengte van zijn zijkanten), waarmee het wordt voortgezet door eenvoudige geometrie om zijn volume te berekenen. De atomen daarentegen zijn degenen die de cel definiëren, dus het is mogelijk om de dimensies van hetzelfde uit de atomaire radio's uit te drukken, zoals in de volgende secties te zien is.

Het kan je van dienst zijn: racemische mix: chiraliteit, voorbeelden

Met betrekking tot het volume van atomen, het totale aantal dat aanwezig is in de eenheidscel (1, 2, 3, enz.), evenals zijn bolvormige geometrie. Daarom is de formule een beetje gewijzigd:

Ugly = (nº atomen) (atoomvolume)/ (eenheidscelvolume)

Om lelijk te berekenen, moet u dan bepalen nr., V_atoom en v_Eenheidscel.

Eenvoudige kubieke

Eenvoudige kubieke eenheidscel. Bron: CCC_CRYSTAL_CELL_ (Opaque).Svg: *cobique_centre_atomes_par_maille.SVG: CDANG (origineel idee en SVG-uitvoering), Samuel Dupré (3d Odeling met SolidWorks) Leid werk: Daniele Pugliesi (Talk) Leid werk: Daniele Pugliesi, CC BY-SA 3.0, via Wikimedia Commons

De eenvoudigste eenheidscel van alles is de eenvoudige kubieke. Daarin hebben we enkele delen van atomen in elk van de hoeken. Als we het zien, zullen we dat de lengte opmerken naar Van deze cel is het gelijk aan 2R, omdat het de atomen zijn die de cel definiëren. Dus het volume van de eenheidscel is gelijk aan:

V_Eenheidscel = naar³ (volume van een kubus)

= (2r)³

= 8r³

Ondertussen zal het volume van het atoom gelijk zijn aan:

V_atoom = (4/3) πr³ (volume van een bol)

Elk van de hoeken wordt gedeeld door nog een 8 aangrenzende eenheidscellen. Daarom hebben we een 1/8 fractie in elke hoek, en met 8 van hen geven we geen 1 atoom per eenheidscel (1/8 x 8 = 1).

De verpakkingsfactor is:

Ugly = (1) (4/3) πr³ /8r³

= π/6 ≈ 52%

Dat wil zeggen, in een eenvoudige kubieke cel bezetten de atomen 52% van het gehele glasvolume.

Kubiek gecentreerd in het lichaam

Bepaling van het celvolume

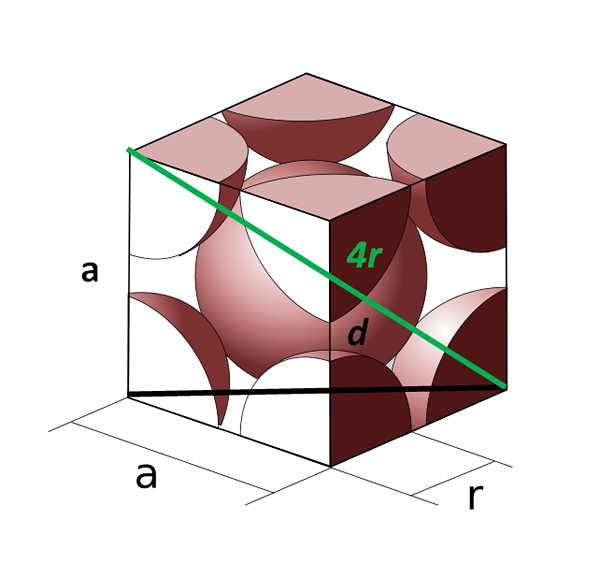Lichaamsunitaire cel gecentreerd op het lichaam. Bron: cobique_centre_atomes_par_maille.SVG: CDANG (origineel idee en SVG-uitvoering), Samuel Dupré (3d Odeeling met SolidWorks) Derivatief werk: Daniele Pugliesi, CC BY-SA 3.0, via Wikimedia Commons

Laten we nu eens kijken naar de kubieke cel op het lichaam. De kant naar Het kan niet langer gelijk zijn aan 2R, omdat we een lege ruimte hebben tussen de twee atomen van de hoeken. Er is daarom een ​​diagonaal D gelijk aan 4r (groene kleur) die de cel door het midden kruist en de tegenoverliggende hoeken aanraakt, en een andere diagonaal D van het gezicht (zwart).

De zijkanten naar, D en 4R Teken een rechthoekige driehoek waarop we trigonometrie kunnen toepassen om te berekenen wat de waarde is van naar:

(4R)² = D² + naar²

Kan u van dienst zijn: intermoleculaire krachten

Maar aan de andere kant hebben we aan de basis van de eenheidscel nog een driehoek (naar, naar En D) waaraan we de hypotenuse kunnen berekenen:

D²  = A² + naar²

= 2a²

Vervangen dan zullen we hebben:

(4R)² = (2e²) + a²

(4R)² = 3a²

A = (4/√3) r

De V_Eenheidscel is gelijk aan:

V_Eenheidscel = A³

= ((4/√3) r)³

Bepaling van de verpakkingsfactor

Merk op dat we met betrekking tot het aantal atomen 1 atoom in deze cel hebben, na dezelfde aftrek gemaakt voor de eenvoudige kubieke cel en een ander extra atoom dat zich in het midden van de cel bevindt. Er zijn dus in totaal 2 atomen voor elke kubieke cel gecentreerd op het lichaam.

De verpakkingsfactor is dan:

Ugly = (2) (4/3) πr³ / ((4/ √3) r)³

= (√3/8) π ≈ 68%

Dat wil zeggen, in een kubieke cel gericht op het lichaam, wordt 68% van het glazen volume bezet door atomen. Bijgevolg is deze kristallijne opstelling compacter (of dicht) dan de eenvoudige kubieke.

Kubiek gecentreerd op gezichten

Bepaling van het celvolume

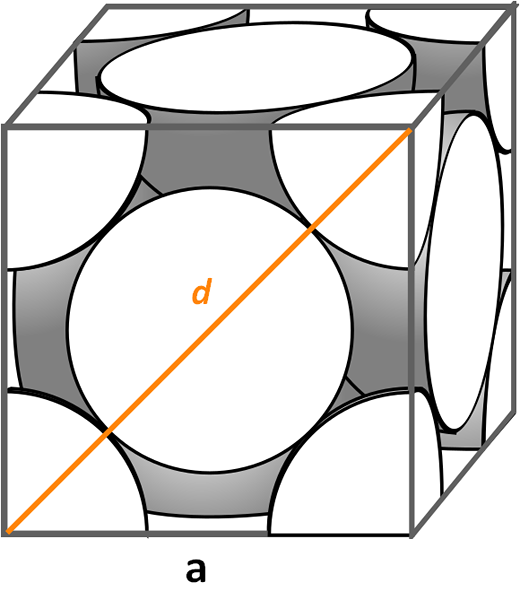Kubieke eenheidscel gecentreerd op gezichten. Bron: CDANG, CC BY-SA 3.0, via Wikimedia Commons

Laten we eens kijken naar de kubieke eenheidscel gecentreerd op gezichten, heel gebruikelijk in symfines van anorganische zouten en sommige metalen, zoals goud en zilver. Om de verpakkingsfactor te bepalen, moeten we beginnen met de vorige voorbeelden om te vinden wat het volume van de eenheidscel is. Het is noodzakelijk om de zijkant opnieuw te berekenen naar En dus het volume van de kubus naar³.

Deze keer is de procedure eenvoudiger en directer, omdat we een diagonaal hebben D Vooraan, samen met de zijkanten naar, Ze vormen een juiste driehoek waarop we trigonometrie kunnen toepassen:

D² = A² + naar²

= 2a²

Opruiming naar we zullen hebben:

naar = D/√2

Maar dat merken we visueel op D Het is gelijk aan 4R, dus we maken een vervanging:

naar = 4r/√2

= 2R 2^1-1/2

= (2√2) r

Zijn v_Eenheidscel gelijk aan:

naar³ = ((2√2) r)³

= (16√2) r³

Wat betreft het aantal atomen per cel, hebben we acht delen van één atoom in elke hoek, en ook een helft van atoom voor elk van de zes gezichten, die wordt gedeeld door een andere aangrenzende cel. Daarom is het aantal atomen gelijk aan:

Nº atomen = 1/8 (8) + 1/2 (6) = 1 + 3 = 4

Bepaling van de verpakkingsfactor

Omdat er 4 atomen zijn in elke kubieke cel gericht op gezichten, en ook het volume, dat gelijk is aan (16√2) r³, We kunnen vervolgens de verpakkingsfactor berekenen:

Ugly = (nº atomen) (atoomvolume)/ (eenheidscelvolume)

= (4) (4/3) πr³ / (16√2) r³

Het kan u van dienst zijn: Acilo Group: structuur, kenmerken, verbindingen en derivaten

= π/(3√2) ≈ 74%

Merk op dat deze cel nog compacter is dan de vorige: 74% van het totale volume van de cel wordt bezet door atomen. In een perfect en puur kristal zou dit gelijk zijn aan te zeggen dat 26% van het volume beschikbaar is om andere gastatomen te hosten.

Compact zeshoekig

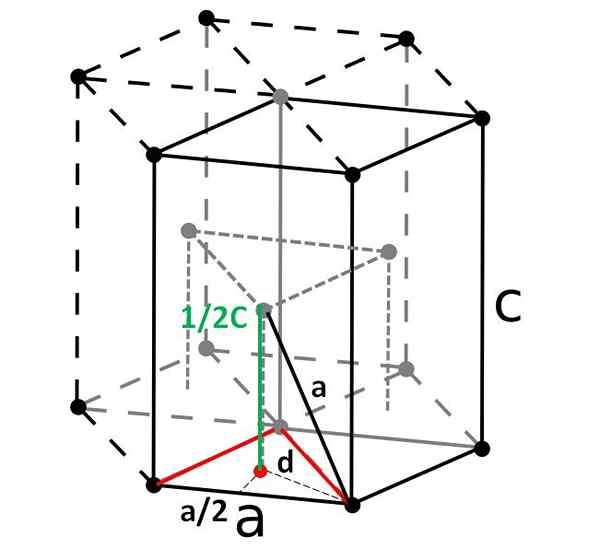Compacte zeshoekige cel en zijn rhombohedrale primitieve cel. Bron: Origineel: Dornelfvector: Depiep, CC BY-SA 3.0, via Wikimedia Commons

Ten slotte hebben we onder de eenvoudigste en meest compacte eenheidscellen de compacte zeshoekige. In tegenstelling tot de vorige is de berekening van het volume iets omslachtiger. Zoals te zien is, is het niet kubiek, dus het heeft twee parameters naar En C, De laatste is de hoogte van de cel.

Bepaling van de hoogte van de cel

De zeshoekige cel kan worden opgesplitst in drie rhomboyan -cellen, en van een van hen zal deze worden berekend naar En C. De kant naar, Hoewel niet zo duidelijk in de afbeelding hierboven, is het gelijk aan 2r. Rekenen C, In plaats daarvan gebruiken we de driehoek en het rode puntproduct van het interne driehoekige prisma van dezelfde cel.

We moeten de afstand berekenen D Om te kunnen bepalen hoeveel het waard is C. Op de vloer is de rode driehoek gelijkzijdig, met een hoek van 60º. Maar als een andere interne rechthoekige driehoek wordt overwogen met zijden naar/2 en D, en een hoek van 30º (half), dan kunnen we door trigonometrie bepalen D:

Cos (30º) = (naar/2) / D

D = naar/√3

En nu beschouwen we de juiste driehoek die uit de zijkanten bestaat C/2 (groen), naar (zwart en D (gestippeld):

naar² = (naar/√3)² + (C/2)²

Opruiming C We zouden hebben:

C = √ (8/3) naar

En vervangen naar Door 2r:

C = √ (8/3) (2r)

= √ (4 · 2/3) (2r)

= 4√ (2/3) r

Bepaling van het celvolume

Om het volume van de zeshoekige cel te bepalen, moet je het zeshoekgebied vermenigvuldigen met zijn hoogte. Wetende dat gelijkzijdige driehoeken partij hebben naar, De hoogte wordt berekend H. Dus het vinden van het gebied van een driehoek, wat voor deze zaak is √3/4naar², We vermenigvuldigen deze waarde met 6 om het zeshoekgebied te verkrijgen: 3 (√3/2)naar²

Het volume is daarom:

V_Eenheidscel = Zeshoekige gebied x hoogte

= 3 (√3/2)naar² X 4√ (2/3) r

En opnieuw vervangen naar Door 2r:

V_Eenheidscel  = 3 (√3/2) (2R)² X 4√ (2/3) r

= 24√2 r³

Bepaling van de verpakkingsfactor

In de zeshoekige cel zijn er 12 atomen in de hoeken, die 1/6 van hun volumes binnen hebben. Er zijn ook 3 interne atomen waarvan de volumes compleet zijn, en nog eens 2 atomen op de bovenste en onderste gezichten waarvan de helft van zijn volumes zich in de cel bevinden.

Daarom is het aantal atomen gelijk aan:

Nº atoom = 1/6 (12) + 1 (3) + 1/2 (2) = 6 atomen

En de verpakkingsfactor is eindelijk:

Ugly = (nº atomen) (atoomvolume)/ (eenheidscelvolume)

= (6) (4/3) πr³ / 24√2 r³

= π/(3√2) ≈ 74%

Merk op dat de compartimentfactor voor de zeshoekige cel hetzelfde is als voor de kubieke cel gecentreerd op gezichten. Dat wil zeggen, beide zijn even compact.

Referenties

1. C. Barry Carter & M. Grant Norton. (2007). Keramische materialen wetenschap en engineering. Springer.
2. Shiver & Atkins. (2008). Anorganische scheikunde. (Vierde druk). MC Graw Hill.
3. Whitten, Davis, Peck & Stanley. (2008). Scheikunde. (8e ed.)). Cengage leren.
4. Wikipedia. (2021). Atomaire pakkingsfactor. Opgehaald uit: in.Wikipedia.borg
5. Brandon. (2021). Wat is atomaire verpakkingsfactor (en hoe deze te berekenen voor SC, BCC, FCC en HCP)? Materials Science & Engineering Student. Hersteld van: msestudent.com