Samendrukbaarheidsfactor hoe te berekenen, voorbeelden en oefeningen te berekenen

Hij Samendrukbaarheidsfactor z, o Compressiefactor voor gassen, is een dimensieloze waarde (zonder eenheden) die wordt geïntroduceerd als een correctie in de statusvergelijking van de ideale gassen. Op deze manier lijkt het wiskundige model meer op het waargenomen gedrag van gas.

In het ideale gas is de toestandsvergelijking die betrekking heeft op de variabelen P (druk), V (volume) en T (temperatuur): P.V _ideaal = n.R.T met n = aantal mol en r = constante van de ideale gassen. Door de correctie van de z -comprimerende factor toe te voegen, wordt deze vergelijking omgezet in:

P.V = z.N.R.T

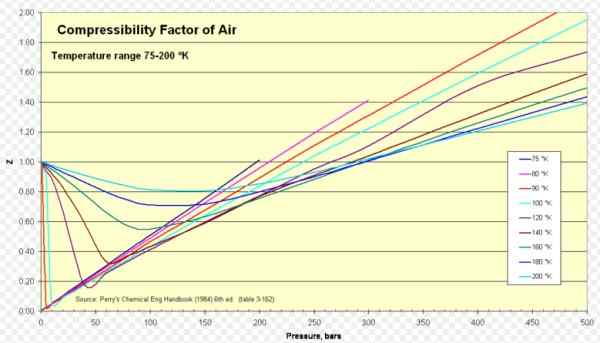
Figuur 1. Luchtcompressibiliteitsfactor. Bron: Wikimedia Commons. https: // upload.Wikimedia.org/wikipedia/commons/8/84/compressibility_factor_of_air_75-200_k.PNG.

[TOC]

Hoe de samendrukbaarheidsfactor te berekenen?

Rekening houdend met dat molaire volume is V_koel = V/n, Je hebt het echte molaire volume:

P . V_echt = Z. R. T → Z = PV _echt/RT

Aangezien de Z -samendrukbaarheidsfactor afhankelijk is van gasomstandigheden, wordt deze uitgedrukt als een functie van druk en temperatuur:

Z = z (p, t)

Als u de eerste twee vergelijkingen vergelijkt, wordt opgemerkt dat als het aantal mol N gelijk is aan 1, het molaire volume van een echt gas gerelateerd is aan dat van het ideale gas door:

V_echt / V_ideaal = Z → V _echt = Z V_ideaal

Wanneer de druk de 3 atmosferen overschrijdt, stopt de meeste gassen zich te gedragen als ideale gassen en het echte volume verschilt aanzienlijk van het ideaal.

Dit realiseerde in zijn experimenten de Nederlandse fysicus Johannes van der Waals (1837-1923), waardoor hij een model creëerde dat beter is aangepast aan de praktische resultaten dan de vergelijking van ideale gassen: de staatsvergelijking van van der Waals.

Kan u van dienst zijn: natriumoxalaat (NA2C2O4): structuur, eigenschappen, gebruik, risico's

Voorbeelden

Volgens de vergelijking P.V_echt= Z.N.RT, Voor een ideaal gas, z = 1. In echte gassen doet echter door het verhogen van de druk ook de waarde van z. Dit is logisch omdat bij grotere drukgasmoleculen meer mogelijkheden hebben om te botsen, daarom nemen de afstotingskrachten toe en daardoor het volume.

Aan de andere kant om de druk te verlagen, bewegen de moleculen met een grotere vrijheid en nemen de afstotingskrachten af. Daarom wordt een lager volume verwacht. Wat betreft de temperatuur, wanneer deze stijgt, neemt Z af.

Zoals Van der Waals opmerkte, wordt in de buurt van het zo -aangedekte kritieke punt het gasgedrag erg afgeleid van een ideaal gas.

Het kritieke punt (t_C, P_C) van elke stof zijn de druk- en temperatuurwaarden die hun gedrag bepalen vóór een faseverandering:

-T_C Het is de temperatuur waarboven het gas in kwestie niet vloeibaar is.

-P_C  Het is de minimale druk die nodig is om het gas te vloeibaar te maken bij temperatuur T_C

Elk gas heeft echter zijn eigen kritieke punt, dat de temperatuur definieert en een verminderde druk T_R En P_R als volgt:

P_R = P / P_C

V_R = V /V_C

T_R = T /T_C

Er wordt waargenomen dat een gas beperkt is met identiek V_R En T_R oefen dezelfde druk uit P_R. Om deze reden, als Z grafisch is, afhankelijk van P_R naar dezelfde T_R, Elk punt in die curve is hetzelfde voor elk gas. Dit heet Principe van overeenkomstige toestanden.

De samendrukbaarheidsfactor in ideale gassen, lucht, waterstof en water

Hieronder is een samendrukbaarheidscurve voor verschillende gassen bij verschillende verlaagde temperaturen. Dan enkele voorbeelden van z voor sommige gassen en een procedure om Z te vinden met behulp van de curve.

Kan u van dienst zijn: waterstof: geschiedenis, structuur, eigenschappen en gebruik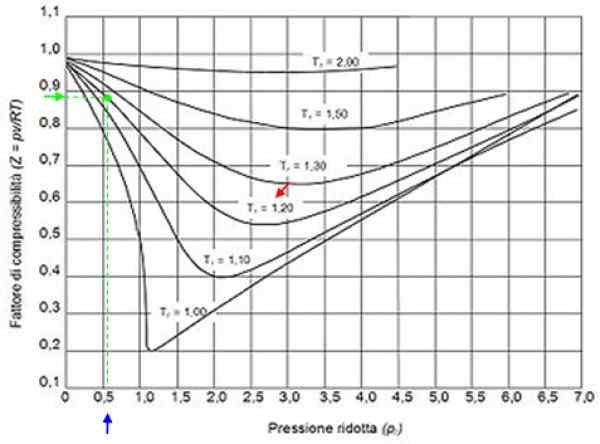Figuur 2. Grafische factorafbeeldingen voor gassen volgens reductiedruk. Bron: Wikimedia Commons.

Ideale gassen

De ideale gassen hebben z = 1, zoals in het begin uitgelegd.

Lucht

Voor lucht Z is ongeveer 1 in een uitgebreid bereik van temperaturen en drukken (zie figuur 1), waar het ideale gasmodel zeer goede resultaten geeft.

Waterstof

Z> 1 voor alle drukken.

Water

Om z van het water te vinden, zijn de waarden van het kritieke punt nodig. Het kritieke punt van water is: P_C = 22.09 MPA en T_C= 374.14 ° C (647.3 K). Nogmaals is het noodzakelijk om rekening te houden met dat de Z -samendrukbaarheidsfactor afhangt van de temperatuur en druk.

Stel bijvoorbeeld dat u Z uit het water wilt vinden bij 500 ºC en 12 MPa. Dan is de eerste om de verminderde temperatuur te berekenen, waarvoor de Celsius -graden moeten worden doorgegeven aan Kelvin: 50 ºC = 773 K:

T_R = 773/647.3 = 1.2

P_R = 12/22.09 = 0.54

Met deze waarden vinden we in de grafiek van de figuur de curve die overeenkomt met t_R = 1.2, aangegeven met een rode pijl. Dan kijken we in de horizontale as de waarde van P_R Dichter bij 0.54, gemarkeerd in blauw. Nu tekenen we een verticaal totdat we de T -curve onderscheppen_R = 1.2 en ten slotte wordt het vanaf dat punt geprojecteerd op de verticale as, waar we de geschatte waarde van z = 0 lezen.89.

Opgeloste oefeningen

Oefening 1

Er is een gasmonster bij een temperatuur van 350 K en een druk van 12 atmosferen, met een molair volume dat 12 % hoger is dan de voorspelde door de ideale gassenwet. Berekenen:

A) Z Compressiefactor.

b) Molair gasvolume.

Kan u van dienst zijn: onomkeerbare reactie: kenmerken en voorbeelden

c) Volgens de bovenstaande resultaten geven aan welke de dominante krachten in dit gasmonster zijn.

Gegevens: r = 0,082 l.ATM/MOL.K

Oplossing voor

Wetende dat V _echt  is 12 % hoger dan V_ideaal :

V_echt  = 1.12V_ideaal

Z = v _echt / V_ideaal = 1.12

Oplossing B

P . V_echt = Z. R. T → V_echt = (1.12 x 0.082 x 350 /12) l /mol = 2.14 l/mol.

Oplossing C

De afstotingskrachten zijn die overheersen, omdat het volume van het monster toenam.

Oefening 2

Er zijn 10 mol ethaan beperkt in een volume van 4.86 L A 27 ºC. Zoek de druk uitgeoefend door ethaan uit:

a) het ideale gasmodel

b) De van der Waals -vergelijking

c) Zoek de compressiefactor uit de vorige resultaten.

Gegevens voor ethaan

Van der Waals coëfficiënten:

A = 5.489 DM⁶. Geldautomaat . mol^-2  en B = 0.06380 DM³. mol^-1.

Kritische druk: 49 atm. Kritische temperatuur: 305 K

Oplossing voor

De temperatuur wordt doorgegeven aan Kelvin: 27 º C = 27 +273 K = 300 K, onthoud ook dat 1 liter = 1 l = 1 dm³.

Vervolgens worden de gegevens in de ideale gasvergelijking vervangen:

P.V = n.R.T → p = (10 x 0,082 x 300/4.86 l) ATM = 50.6 atm

Oplossing B

De statusvergelijking van van der Waals is:

Waar a en b de coëfficiënten zijn die door de verklaring worden gegeven. Bij het opruimen van P:

Oplossing C

We berekenen de verminderde druk en temperatuur:

P_R = 35.2/49 = 0.72

T_R = 300/305 = 0.98 ≈ 1

Met deze waarden wordt de waarde van z in de grafiek van figuur 2 gezocht, en constateert dat Z ongeveer 0 is.7.

 Referenties

1. Atkins, P. 199999. Fysische chemie. Omega -edities.
2. Cengel, en. 2012. Thermodynamica. 7^ma Editie. McGraw Hill.
3. Engel, T. 2007. Inleiding tot fysicochemie: thermodynamica. Pearson.
4. Levine, ik. 2014. Principles van natuurkunde-chemie. 6e. Editie. McGraw Hill.
5. Wikipedia. Samendrukbaarheidsfactor. Opgehaald uit: in.Wikipedia.borg.