Zijn er scalene driehoeken met een rechte hoek?

Er zijn veel scalele -driehoeken met een rechte hoek. Voordat u over het onderwerp gaat, is het eerst nodig om de verschillende soorten driehoeken te kennen die bestaan. De driehoeken worden geclassificeerd door twee klassen die zijn: hun interne hoeken en de lengte van hun zijden.

De som van de interne hoeken van een driehoek is altijd gelijk aan 180º. Maar volgens interne hoeken worden maatregelen geclassificeerd als:

-Verbinden: Die driehoeken zijn zodanig dat hun drie hoeken acuut zijn, dat wil zeggen, ze meten elk minder dan 90 °.

-Rechthoek: Zij zijn die driehoeken met een rechte hoek, dat wil zeggen een hoek die 90 ° meet, en daarom zijn de andere twee hoeken acuut.

-Stomp: Ze zijn de driehoeken met een stompe hoek, dat wil zeggen een hoek waarvan de maatregel groter is dan 90 °.

Scalan -driehoeken met een rechte hoek

De interesse in dit deel is om te bepalen of een scaleense driehoek een rechte hoek kan hebben.

Zoals hierboven gezegd, is een rechte hoek een hoek waarvan de maat 90º is. Het is alleen nodig om de definitie van een scaleense driehoek te kennen, die afhankelijk is van de lengte van de zijkanten van een driehoek.

Classificatie van driehoeken volgens hun partijen

Volgens de lengte van hun zijden zijn de driehoeken geclassificeerd als:

-Gelijkzijdig: Ze zijn al die driehoeken zodanig dat de lengte van hun drie kanten hetzelfde zijn.

-Gelijkbenig: Het zijn de driehoeken die precies twee kanten van gelijke lengte hebben.

-Scaleen: Het zijn die driehoeken waarop de drie partijen verschillende maatregelen hebben.

Formulering van een equivalente vraag

Een vraag die gelijkwaardig is aan die van de titel is: “Zijn er driehoeken met alle drie de zijden met verschillende maatregelen en dit heeft een hoek van 90 °?"

Het antwoord zoals in het begin vermeld is ja. Het is niet erg moeilijk om dit antwoord te rechtvaardigen.

Indien zorgvuldig waargenomen, is geen rechthoekige driehoek gelijkzijdig, dit kan gerechtvaardigd worden dankzij Pythagoras -stelling voor rechthoekige driehoeken, die zegt:

Gegeven een rechthoekige driehoek dat de lengtes van hun categorieën "A" en "B" zijn, en de lengte van de hypotenuse is "C", je moet C² = A²+B², die te zien is dat de lengte van de hypotenuse " C "is altijd groter dan de lengte van elk been.

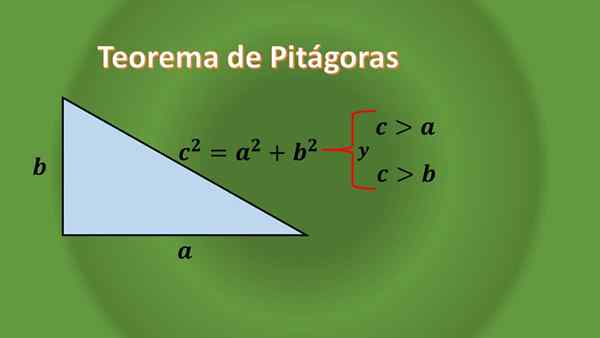
Omdat er niets wordt gezegd over "A" en "B", dan houdt dit in dat een juiste driehoek gelijkmatig of scaleen kan zijn.

Kies vervolgens gewoon elke rechthoekige driehoek zodanig dat de benen verschillende maatregelen hebben, en dus zal een scaleense driehoek met een rechte hoek zijn gekozen.

Voorbeelden

-Als een rechthoekige driehoek wordt overwogen waarvan de benen lengtes van respectievelijk 3 en 4 hebben, dan kan door de Pythagoras -stelling worden geconcludeerd dat de hypotenuse een lengte van 5 zal hebben. Dit houdt in dat de driehoek scaleen is en een rechte hoek heeft.

-Laat ABC een rechthoekige driehoek zijn met metingen van metingen 1 en 2. Dan is de lengte van zijn hypotenuse √5, wat concludeert dat ABC een scaleense rechthoekige driehoek is.

Niet elke schaal driehoek heeft een rechte hoek. Je kunt een driehoek beschouwen zoals die van de volgende figuur, die scaleen is, maar geen van zijn interne hoeken is recht.

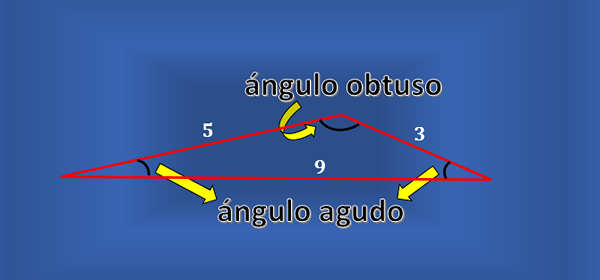Bovendien is niet elke rechte driehoek scaleen. Als u een juiste driehoek beschouwt waarvan de benen beide 1 meten, dan heeft de hypotenuse een maat voor √2. Daarom is de rechthoekige driehoek gelijkbenig.