Bolle spiegel

Wat is een convexe spiegel?

Hij Bolle spiegel Of divergent is een gebogen spiegel, bijna altijd bolvormig en met het reflecterende oppervlak aan de buitenkant van de bol, zoals de ornamenten van de kerstboom. Dankzij convexe spiegels is het mogelijk.

De spiegels die op straat worden geplaatst om de doorvoer van de voertuigen in smalle kruisen te vergemakkelijken, zijn bijvoorbeeld convex, omdat ze een beeld produceren met een breed gezichtsveld.

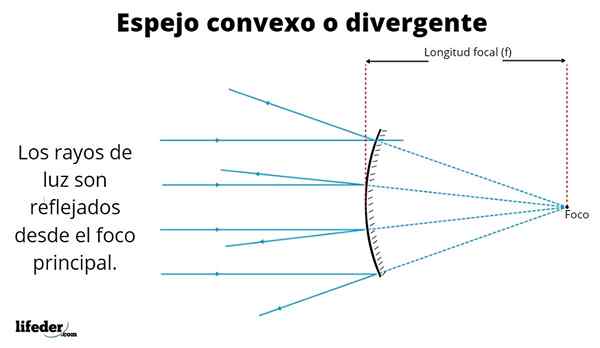
Illustratie van een convexe spiegel

De aldus gevormde beelden zijn divers, afhankelijk van de plaats waar het object wordt geplaatst. Het superieure beeld toont parallelle stralen van een verre fontein zoals de zon.

De stralen worden weerspiegeld op basis van de reflectiewet, die aangeeft dat de invalshoek van de bliksem hetzelfde is waarmee deze wordt weerspiegeld. Zoals we kunnen zien, worden de gereflecteerde stralen gescheiden - ze kruisen niet - wanneer ze het spiegelende oppervlak verlaten, daarom is dit soort spiegel ook bekend als bekend als afwijkend.

Wanneer de reflecties zich uitstrekken van de spiegel - discontinue lijnen in de figuur - deze kruisen op een punt dat focus wordt genoemd.

Kenmerken van convexe spiegels

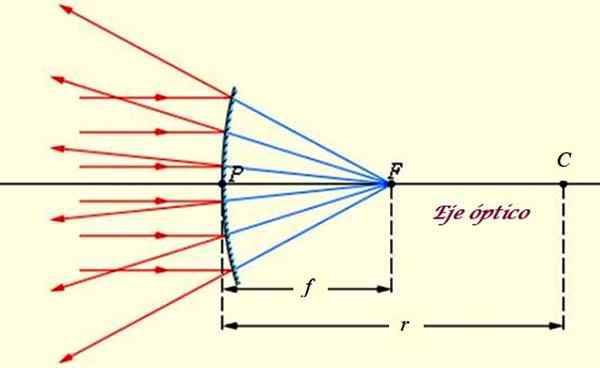
Convex of uiteenlopende spiegel, waarop de stralen van een verre fontein zoals de zon beïnvloeden. Bron: f. Zapata.

De convexe spiegel heeft de volgende kenmerken (zie superieure afbeelding):

-De opmerkelijke punten van de spiegel zijn:

• C Het midden, dat samenvalt met het midden van de bol waartoe de spiegel behoort.
• F De focus, waar de stralen achter de spiegel weerspiegelden samenkomen.
• Het hoekpunt P van hetzelfde, dat overeenkomt met het midden van het bolvormige oppervlak en collineisch is met C en F.

Kan u van dienst zijn: ío (satelliet)

-Heeft optische as of Hoofdas, dat is de lijn loodrecht op het spiegelende oppervlak. De stralen die de optische as beïnvloeden, worden weerspiegeld in dezelfde richting.

-Het midden van de bol waartoe de spiegel behoort, staat op punt C en R is de straal. Een C staat bekend als Krommingscentrum, terwijl R is hij Krommingstraal en geeft aan hoe gebogen de spiegel is: een minderjarige R, meer geaccentueerd is de convexe vorm.

-Het snijpunt van de gereflecteerde stralen staat bekend als Brandpunt van de spiegel. De afstand tussen F en P is ongeveer R/2:

F = r/2

Deze uitdrukking is geldig voor spiegels waarvan de grootte veel lager is dan de krommingsradius.

-De afbeelding die zich vormt, is kleiner en ook virtueel, omdat het zich achter de spiegel bevindt, zoals we daarna zullen zien.

Beeldvorming in de convexe spiegel

Om te weten hoe het beeld dat wordt gevormd in de convexe spiegel de straalbehandeling is, die bestaat uit het weergeven van de lichtstralen die uit het object komen door rechte lijnen.

Deze stralen worden weerspiegeld op het oppervlak van de spiegel en de gereflecteerde stralen worden ook getekend. De straalmethode is van toepassing op elke vorm van spiegel, niet alleen convexes.

Door de gereflecteerde stralen te verlengen, kruisen ze op een bepaald punt, en dat is precies waar het beeld wordt gevormd. De uitbreiding van de gereflecteerde stralen die uit een uitgebreid object als een boom komen, wordt in de onderste figuur weergegeven door discontinue lijnen.

In de onderste figuur worden drie stralen uit het object getekend, zeer bijzonder en gemakkelijk te tekenen, evenals de reflecties:

Kan u van dienst zijn: thermische verwijding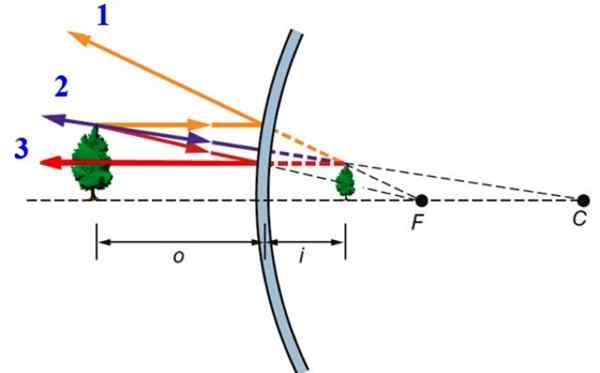 Figuur 2.- Beeldvorming in de convexe spiegel. Bron: f. Zapata.

-Ray 1, dat parallel aan de optische as treft.

-Ray 2, die de exolitatie van de gereflecteerde straal beïnvloedt, gaat precies door de focus van de spiegel, dat wil zeggen punt F. Deze straal wordt parallel aan de optische as weerspiegeld.

-Eindelijk Ray 3, dat loodrecht op het bolvormige oppervlak bereikt, en om deze reden wordt het weerspiegeld in dezelfde richting.

In principe is deze procedure van toepassing op elk punt van de boom, maar met de informatie verkregen uit de 3 getekende stralen is het voldoende om het beeld van het object te vinden: het is gevormd achter de spiegel, het is goed en kleiner dan het origineel.

Voorbeelden en toepassingen van convexe spiegels

Veel zeer getrokken sferische oppervlakken fungeren als convexe spiegels, bijvoorbeeld heldere en zilveren kerstversiering, evenals nieuwe en heldere stalen lepels.

Ook convexe spiegels hebben bijvoorbeeld veel praktische toepassingen, bijvoorbeeld:

Spiegels om verkeersongevallen te voorkomen

Convexe spiegels in straten en wegen helpen ongevallen te voorkomen, omdat ze je in staat stellen het verkeer dat uit de hoeken komt te zien.

Surveillance Mirrors

In winkels en banken zijn er meestal convexe spiegels om dieven te detecteren, en om botsingen tussen mensen en vorkheftruckvoertuigen te vermijden die in de gangen en tussen de planken circuleren.

Achteruitkijkspiegels

Auto's en motorfietsen hebben convexe spiegels, die iets kleinere beelden produceren, maar meer gezichtsveld bedekken dan platte spiegels.

Cassegrain Telescope

Een van de spiegels van de Cassegrain -reflector, de secundaire spiegel, is convex, hoewel deze niet bolvormig is en dient om het beeld te weerspiegelen naar de hoofdspiegel van de telescoop.

Kan u van dienst zijn: Gravitational Energy: formules, kenmerken, toepassingen, oefeningen

Convexe spiegelvergelijkingen

Overweeg de rechthoeken van de volgende figuur, bepaald door straal 1, die van de bovenkant van de pijl komt, de reflectie ervan en de uitbreiding hiervan.

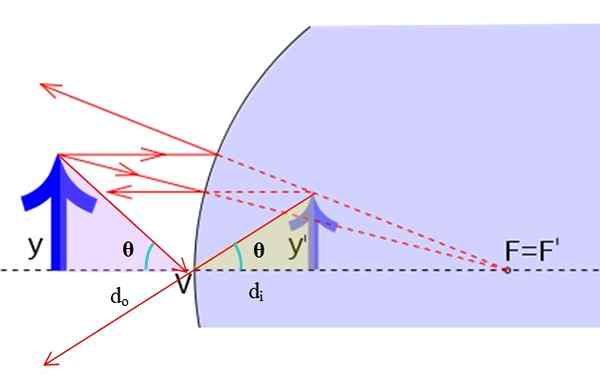Geometrie om de spiegelvergroting te vinden. Bron: f. Zapata.

De originele afbeelding heeft hoogte en, hoewel de hoogte van de virtuele afbeelding is en ' . Is het waar dat:

Tan θ = y/d_of = Y '/d_Je

Spiegelvergroting

De reden tussen de hoogte van de afbeelding en de hoogte van het object is de spiegelvergroting, Het wordt dat genoemd, zelfs als het verkregen beeld kleiner is dan het echte object. We duiden het aan door M:

M = y '/ y = d_Je /D_of

Relatie tussen het object en zijn beeld in de convexe spiegel

Laten we nu deze andere figuur beschouwen, waarbij het AVF -gebied ongeveer als een rechterdriehoek kan worden beschouwd, omdat de kromming van de spiegel niet erg uitgesproken is. Daarom:

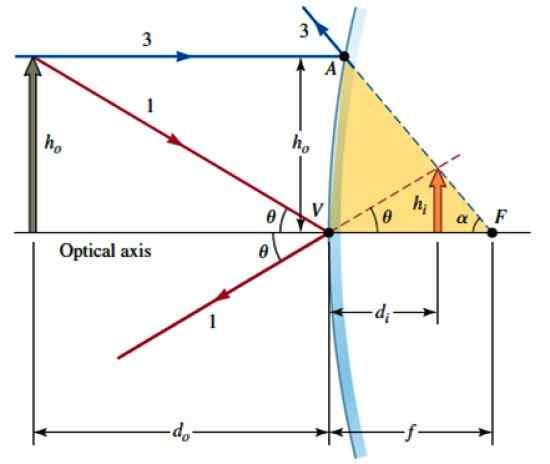Geometrie om de wiskundige relatie tussen het object en het beeld ervan te vinden. Bron: Katz, D. Natuurkunde voor wetenschappers en ingenieurs.

AV ≈ H_of

Dus:

Tan α = h

Daarom:

De omgekeerde van deze uitdrukking is de vergroting, dan:

Daarom:

1- (D_Je /f) = D_Je /D_of

Door alles te delen tussen D_Je:

Eindelijk:

 Nu, voor spiegels zijn enkele tekenconventies van toepassing. Hoewel we weten dat een afstand altijd positief is, worden ze op alle afstanden achter de spiegel onderscheiden met een negatief teken.

Daarom, als F En D_Je Ze zitten achter de spiegel, ze worden een bord minder geplaatst, terwijl voor de afstand D_of Dat is niet nodig, omdat het voor de spiegel loopt. De vorige vergelijking blijft dus:

Het kan worden aangetoond dat deze vergelijking ook geldig is voor de concave spiegel.

Referenties

1. Bauer, W. 2011. Fysica voor engineering en wetenschappen. Deel 2. MC Graw Hill.
2. Giambattista, een. 2010. Natuurkunde. 2e. ED. McGraw Hill.
3. Katz, D. 2017. Natuurkunde voor wetenschappers en ingenieurs. Cengage leren.
4. Thomas, W. 2008. Conceptuele fysica. McGraw Hill.
5. Tippens, p. 2011. Fysica: concepten en toepassingen. 7e editie. McGraw Hill.