Normale inspanning waar het uit bestaat, hoe het wordt berekend, voorbeelden

Hij normale inspanning Toegepast op een bepaald materiaal, ook wel uniaxiale inspanning genoemd, is het de relatie tussen de uitgeoefende kracht loodrecht op een bepaald oppervlak en het kruis -sectionele gebied waarop het werkt, of de belasting per eenheid van het gebied. Wiskundig, als p de grootte van de kracht is en a het gebied is waar het wordt toegepast, is de inspanning σ het quotiënt: σ = p/a.

De eenheden van normale inspanningen in het internationale systeem zijn Newton /Metro², Bekend als Pascal en afgekort PA. Dit zijn dezelfde drukeenheden. Andere eenheden die in de literatuur verschijnen, zijn vaak kilo's / inch² of psi.

Figuur 1. Rotsen worden constant onderworpen aan inspanningen als gevolg van tektonische activiteit, waardoor vervormingen in de aardkorst worden veroorzaakt. Bron: Pixabay.

In figuur 2 worden twee krachten van gelijke grootte loodrecht uitgeoefend op het kruis -sectionele gebied, waardoor een tractie op de zeer lichte balk wordt gemaakt die de neiging heeft om het uit te breiden.

Deze krachten leveren een normale inspanning die ook wordt genoemd Axiale belasting gecentreerd, omdat de werklijn samenvalt met de axiale as, waarop het zwaartepunt zich bevindt.

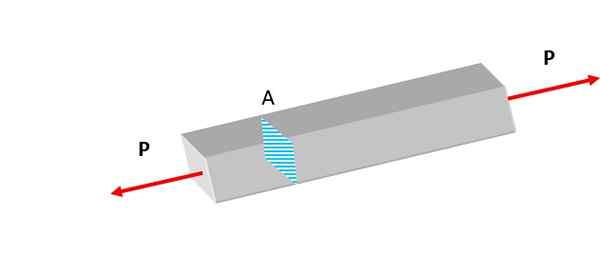Figuur 2. De getoonde balk is onderworpen aan tractiekrachten. Bron: zelf gemaakt.

Inspanningen, of het nu normaal is of andere typen, verschijnen continu in de natuur. In de lithosfeer zijn de rotsen onderhevig aan zwaartekracht en tektonische activiteit, waarbij vervormingen experimenteren.

Op deze manier ontstaan ​​structuren zoals plooien en mislukkingen, wiens studie belangrijk is bij het gebruik van mineralen en civiele techniek, voor de bouw van gebouwen en wegen, om enkele voorbeelden te noemen.

[TOC]

Hoe wordt het berekend?

De vergelijking die aan het begin wordt gegeven σ = P/A maakt het mogelijk om de gemiddelde normale inspanning op het gebied in kwestie te berekenen. De waarde van P is de grootte van de resulterende kracht over het gebied dat op het zwaartepunt wordt toegepast en is voldoende voor veel eenvoudige situaties.

In dit geval is de verdeling van krachten uniform, vooral op punten verwijderd van waar je de lat hebt onderworpen aan tractie of compressie. Maar als de inspanning nodig is om op een specifiek punt te berekenen of de krachten niet gelijkmatig worden verdeeld, is het noodzakelijk om de volgende definitie te gebruiken:

Kan u van dienst zijn: gesloten elektrisch circuit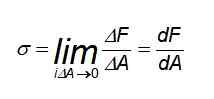

In het algemeen kan de waarde van de inspanning op een bepaald punt verschillen van de gemiddelde waarde. In feite kan de inspanning variëren volgens de sectie om te overwegen.

Dit wordt geïllustreerd in de volgende figuur, waarbij tractiekrachten f proberen de balk in evenwicht te scheiden in de secties mm En nn.

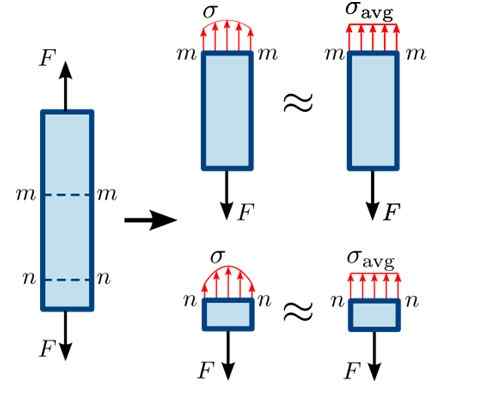figuur 3. Verdeling van normale inspanningen in verschillende secties van een bar. Bron: https: // commons.Wikimedia.org/wiki/bestand: normaal_stress.Svg#/media/bestand: normaal_stress.SVG

Als het gedeelte nn Het ligt heel dicht bij waar kracht F naar beneden, de verdeling van krachten op het oppervlak is niet helemaal homogeen, deze minderjarigen zijn des te verder van dat punt. De verdeling is een beetje meer homogeen in de sectie mm.

In elk geval heeft de normale inspanning altijd de neiging om de twee delen van het lichaam te strekken of te comprimeren die aan beide zijden van het vlak worden gevonden waarop ze handelen. Aan de andere kant hebben andere verschillende inspanningen, zoals afschuiving, de neiging om deze onderdelen te verplaatsen en te scheiden.

Hooke's wet en normale inspanning

De wet van Hooke stelt dat binnen elastische grenzen de normale inspanning recht evenredig is met de vervorming die de bar of het object ervaart. In dat geval:

Normale inspanning ∝ Unitaire vervorming

De evenredigheid constant is de jonge (y) module:

Normale inspanning (σ) = jonge module (y) x unitaire vervorming (ε)

σ = y. ε

Met ε = Δl/l, waarbij Δl het verschil is tussen de uiteindelijke en de beginlengte, die l is.

De jonge module of elasticiteitsmodule is een kenmerk van het materiaal, waarvan de afmetingen hetzelfde zijn als die van de inspanning, omdat de vervorming van de eenheid dimensieloos is.

Het kan u van dienst zijn: 13 voorbeelden van de tweede wet van Newton in het dagelijks leven

Het belang van inspanning in de weerstand van materialen en geologie

Het is erg belangrijk om te bepalen hoe resistent de materialen voor inspanningen zijn. Voor de structuren die worden gebruikt bij de constructie van gebouwen, evenals bij het ontwerpen van onderdelen voor verschillende apparaten, is het noodzakelijk om ervoor te zorgen dat de gekozen materialen goed aan hun functie voldoen.

Daarom worden materialen uitvoerig geanalyseerd in laboratoria door proeven die bestemd zijn om te weten hoeveel kracht ze kunnen weerstaan ​​voordat ze vervormen en breken, waardoor hun functies verloren gaan. Op basis hiervan wordt de beslissing genomen om al dan niet een bepaald stuk te produceren of deel uit te maken van een apparaat.

Er wordt aangenomen dat de eerste wetenschapper die systematisch de weerstand van de materialen bestudeerde, Leonardo Da Vinci was. Hij liet het bewijs achter van proeven waarin hij de weerstand van draden van hangende stenen van verschillende pesos bepaalde.

In pogingen is zowel de grootte van de kracht als ook de dimensies van de structuur en hoe deze wordt toegepast belangrijk, om de limieten vast te stellen waarbinnen het materiaal een elastisch gedrag heeft; dat wil zeggen, het keert terug naar zijn oorspronkelijke vorm wanneer de inspanning ophoudt.

Met de resultaten van deze tests worden inspannings-formatiecurves uitgevoerd voor verschillende soorten materialen, zoals staal, beton, aluminium en nog veel meer.

Voorbeelden

In de volgende voorbeelden wordt aangenomen dat de krachten gelijkmatig worden verdeeld en dat het materiaal homogeen en isotrope is. Dit betekent dat de eigenschappen in elke richting hetzelfde zijn. Daarom is het geldig om de vergelijking σ = P/A toe te passen om inspanningen te vinden.

-Oefening 1

In figuur 3 is bekend dat de gemiddelde normale inspanning die op de AB -sectie werkt, magnitude 48 kPa heeft. Zoek: a) de grootte van de kracht f die werkt in CB, b) de inspanning op sectie BC.

Het kan u van dienst zijn: horizontaal schieten: kenmerken, formules en vergelijkingen, oefeningen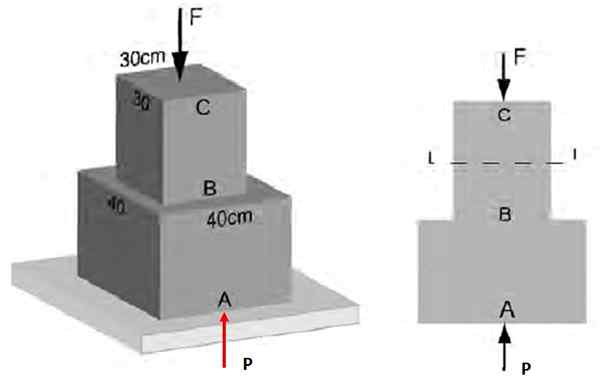Figuur 4. Normale inspanningen op de structuur van voorbeeld 1 ..

Oplossing

Omdat de structuur in statisch evenwicht is, volgens de tweede wet van Newton:

P-f = 0

De normale inspanning op de AB -sectie heeft een grootte:

σ_Aab = P/A_Aab

Waar p = σ_Aab . NAAR_Aab = 48000 PA. (40 x 10 ^-2 M)² = 7680 n

Daarom f = 7680 n

De normale inspanning op sectie BC is de verhouding tussen de grootte van F en het gebied van de dwarsdoorsnede aan die kant:

σ_BC = F/a_BC = 7680 N / (30 x 10 ^-2 M)² = 85.3 kPa.

-Oefening 2

Een draad van 150 m lang en 2.5 mm in diameter wordt uitgerekt door een kracht van 500 N. Vinden:

a) longitudinale inspanning σ.

b) Unitaire vervorming, wetende dat de uiteindelijke lengte 150 is.125 m.

c) de elasticiteitsmodule EN van deze draad.

Oplossing

a) σ = f / a = f / π.R²

De straal van de draad is de helft van de diameter:

R = 1.25 mm = 1.25 x 10^-3 M.

Het kruis -sectie -gebied is π.R², Dan is de inspanning:

σ = f / π.R² = 500 / (π.(1.25 x 10^-3))² PA = 101859.2 PA

b) ε = ΔL / l = (uiteindelijke lengte - initiële lengte) / beginlengte

Daarom:

ε = (150.125 - 150) /150 = 0.125/150 = 0.000833

c) De module van de jonge draad wordt gewist door de eerder berekende waarden van ε en σ te kennen:

Y = σ / ε = 101859.2 PA / 0.000833 = 1.22 x 10⁸ PA = 122 MPA.

Referenties

1. Bier, f. 2010. Materiaalmechanica. 5e. Editie. McGraw Hill. 7 - 9.
2. Giancoli, D.  2006. Fysica: principes met toepassingen. 6^Te  ED. Prentice Hall. 238-242.
3. Hibbeler, R.C. 2006. Materiaalmechanica. 6e. Editie. Pearson Education. 22 -25
4. Valera Negrete, J. 2005. ALGEMENE FYSICA -NOTIES. UNAM. 87-98.
5. Wikipedia. Stress (mechanica). Hersteld van: Wikipedia.borg.