Gravitationele energieformules, kenmerken, toepassingen, oefeningen

De Zwaartekrachtenergie Het is degene die een enorm object heeft wanneer het wordt ondergedompeld in het zwaartekrachtveld dat door een ander wordt geproduceerd. Enkele voorbeelden van objecten met zwaartekrachtenergie zijn: de appel in de boom, de appel die valt, de maan rond de aarde en de aarde in een baan om de zon.

Isaac Newton (1642-1727) was de eerste die zich realiseerde dat zwaartekracht een universeel fenomeen is en dat elk object met massa in zijn omgeving een veld produceert dat in staat is de ene kracht op een andere te produceren.

Figuur 1. De maan die in een baan om de aarde draait, heeft zwaartekrachtenergie. Bron: Pixabay

[TOC]

Formules en vergelijkingen

De kracht waarnaar in Newton wordt verwezen, staat bekend als zwaartekracht en levert energie aan het object waarop het werkt. Newton formuleerde de universele zwaartekrachtwet als volgt:

"Wees twee specifieke massaobjecten M1 en M2 respectievelijk, elk oefent aan de andere een trek van aantrekkingskracht uit die evenredig is met het product van hun massa en omgekeerd evenredig met het kwadraat van de afstand die hen scheidt.".

In de vorige uitdrukking, F Het is de kracht van zwaartekrachtaantrekking die object 1 uitoefent op object 2 (of vice versa), M1 En M2 De respectieve massa's van objecten en R is de afstand die objecten scheidt. G Het is een evenredigheidsconstante bekend als de zwaartekrachtconstante.

Zwaartekrachtenergie OF geassocieerd met zwaartekracht F is:

Let op de aanwezigheid van een negatief teken, wat betekent dat als de scheiding tussen objecten eindig is, de zwaartekrachtenergie negatief is. Maar als de scheiding de neiging heeft oneindig te zijn, is de zwaartekrachtenergie nul.

Een object dat wordt ondergedompeld in een zwaartekrachtveld heeft zwaartekracht potentieel energie OF en kinetische energie K. Als er geen andere interacties zijn, of ze zijn van verwaarloosbare intensiteit, de totale energie EN van dit object is de som van zijn zwaartekrachtenergie plus zijn kinetische energie:

E = k + u

Als een object zich in een zwaartekrachtveld bevindt en andere dissipatieve krachten niet aanwezig zijn, zoals wrijving of luchtweerstand, dan totale energie EN Het is een hoeveelheid die constant blijft tijdens de beweging.

Kenmerken van zwaartekrachtenergie

- Een object heeft zwaartekracht potentieel energie als het alleen in aanwezigheid van het zwaartekrachtveld is geproduceerd door een ander.

- De zwaartekrachtenergie tussen twee objecten groeit naarmate de scheidingsafstand tussen hen groter is.

- Het werk dat wordt uitgevoerd door zwaartekracht is gelijk en in tegenstelling tot de variatie van zwaartekrachtenergie van de uiteindelijke positie ten opzichte van die van de initiële positie.

Het kan u van dienst zijn: wat is de balans van het deeltje? (Met voorbeelden)

- Als een lichaam alleen wordt onderworpen aan de werking van de zwaartekracht, is de variatie van zijn zwaartekrachtenergie gelijk en in tegenstelling tot de variatie van zijn kinetische energie.

- De potentiële energie van een massaobject M op een hoogte H Wat betreft het aardoppervlak is MGH tijden groter dan de potentiële energie op het oppervlak, zijn G de versnelling van de zwaartekracht, voor hoogten H Veel lager dan de terrestrische straal.

Veld- en zwaartekrachtpotentieel

Het zwaartekrachtveld G Het wordt gedefinieerd als zwaartekracht F per massa -eenheid. Het wordt bepaald door een testdeeltje op elk punt van de ruimte te plaatsen en het quotiënt te berekenen tussen de kracht die werkt op het testdeeltje gedeeld door de waarde van zijn massa:

G = F / M

Het zwaartekrachtpotentieel V van een massaobject m als de zwaartekrachtpotentiaalenergie van dat object gedeeld door zijn eigen massa wordt gedefinieerd.

Het voordeel van deze definitie is dat het zwaartekrachtpotentieel alleen afhangt van het zwaartekrachtveld, zodat zodra het potentieel bekend is V, Zwaartekrachtenergie OF van een massaobject M is:

U = m.V 

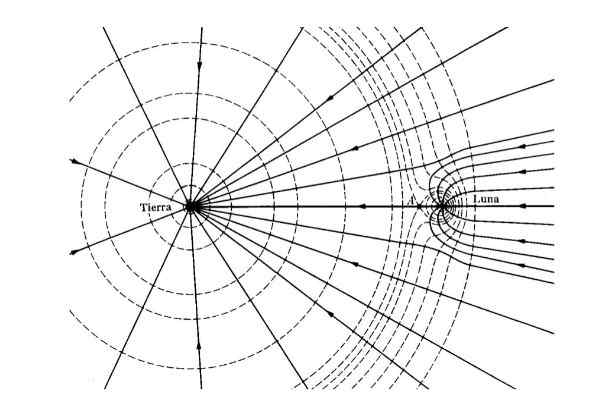Figuur 2. Gravitationaal veld (continue lijnen) en equi -potentieel (gesegmenteerde lijn) voor het Earth - Luna -systeem. Bron: W T Scott, Am. J. Fysiek. 33, (1965).

Toepassingen

Gravitational potentieel energie is wat de lichamen opslaan als ze zich in een zwaartekrachtveld bevinden.

Het water in een tank heeft bijvoorbeeld meer energie in de mate dat de tank hogere hoogte is.

Bij een hogere tank, hoe groter de watersnelheid van de water door de kraan. Dit komt omdat de potentiële water energie op de hoogte van de tank wordt getransformeerd in kinetische waterergie bij de uitgang van de kraan.

Wanneer het water op de top van een berg wordt beschadigd, kan die potentiële energie worden gebruikt om de turbines van de elektriciteitsgeneratie te roteren.

Gravitational Energy verklaart ook getijden. Aangezien de energie- en zwaartekrachtsterkte afhankelijk is van de afstand, is de zwaartekracht van de maan groter in het gezicht van het land dat het dichtst bij de maan ligt dan het verste en meest tegenovergestelde gezicht.

Dit produceert een verschil in krachten die het zeeoppervlak vervormen. Het effect is groter op een nieuwe maan, wanneer de zon en de maan zijn uitgelijnd.

De mogelijkheid om ruimtelijke en satellietstations te bouwen die relatief dicht bij onze planeet blijven, is te wijten aan zwaartekrachtenergie die door de aarde wordt geproduceerd. Als niet ruimtestations en kunstmatige satellieten door de ruimte dwalen.

Het kan u van dienst zijn: Imantation: wat bestaat, methode en voorbeelden

Zwaartekrachtpotentieel van de aarde

Neem aan dat de aarde massa heeft M en een object dat zich op een afstand boven het aardoppervlak bevindt R Wat betreft het centrum van hetzelfde heeft een massa M. 

In dit geval wordt het zwaartekrachtpotentieel bepaald uit zwaartekrachtenergie die eenvoudigweg verdeelt tussen de massa van het object resulterend:

Het zwaartekrachtpotentieel op het aardoppervlak wordt verkregen door te vervangen R Door de terrestrische straal r_T. 

Potentiële energie in de buurt van het aardoppervlak

Stel dat de aarde radio heeft R_T  en massa M.

Zelfs als de aarde geen tijdig object is, is het veld op het oppervlak gelijk aan dat wat zou worden verkregen als al zijn massa M Het was geconcentreerd in het midden, zodat de zwaartekrachtenergie van een object op hoogte H op het aardoppervlak is 

U (r_T + H) = -G.M M (r_T + h)^-1

Maar omdat H veel minder is dan r_T, De vorige uitdrukking kan naderen door 

U = uo + mgh

Waarbij G de versnelling van de zwaartekracht is, waarvan de gemiddelde waarde voor de aarde 9 is.81 m/s^2.

Dan is de potentiële energie -EP van een massa M op de hoogte H op het aardoppervlak:

Ep (h) = u +uo = mgh

Op het aardoppervlak h = 0, dus een object op het oppervlak heeft EP = 0. Gedetailleerde berekeningen zijn te zien in figuur 3.

figuur 3. Gravitationele potentieel energie op een hoogte H op het oppervlak. Bron: voorbereid door F. Zapata.

Opdrachten 

Oefening 1: Gravitationele aarde instorten

Neem aan dat onze planeet een zwaartekracht ineenstortt voor verlies van thermische energie binnen en zijn straal vervalt tot de helft van de huidige waarde, maar de massa van de planeet is constant.

Bepaal wat de versnelling van de zwaartekracht zou zijn nabij het oppervlak van het nieuwe land en hoeveel een overlevende 50 kg-F vóór de ineenstorting wegen. Verhoogt of vermindert de zwaartekrachtenergie van de persoon en in welke factor.

Oplossing

De versnelling van de zwaartekracht op het oppervlak van een planeet hangt af van zijn massa en zijn straal. De zwaartekrachtconstante is universeel en dient ook voor planeten en exoplaneten.

In het geval dat we worden grootgebracht, als de straal van de aarde met de helft wordt verminderd, zou de ernstversnelling van het nieuwe land 4 keer groter zijn. De details zijn te zien op het volgende bord.

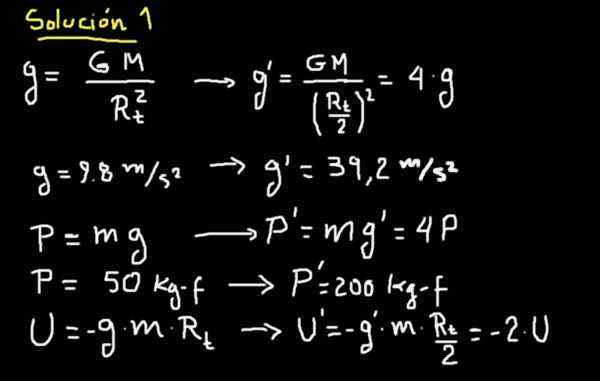
Dit betekent dat een Superman en Survivor die op de oude planeet weegt 50 kg-F 200 kg-F op de nieuwe planeet zal wegen.

Kan u van dienst zijn: thermische balans: vergelijkingen, toepassingen, oefeningen

Aan de andere kant zal de zwaartekrachtenergie met de helft op het oppervlak van de nieuwe planeet zijn verminderd.

Oefening 2: Gravitationele instorting en ontsnappingssnelheid

In verwijzing naar de situatie die in Oefening 1 is verhoogd, wat zou gebeuren met de uitlaatsnelheid: verhoogt, neemt af in welke factor?

Oplossing 2

De uitlaatsnelheid is de minimale snelheid die nodig is om te ontsnappen aan de zwaartekrachtattractie van een planeet.

Om het te berekenen wordt aangenomen dat een projectiel dat met deze snelheid schiet de oneindigheid bereikt met nulsnelheid. Bovendien is de zwaartekrachtenergie in oneindigheid nul. Daarom zal een projectiel dat schiet met de uitlaatsnelheid nul totale energie heeft.

Dat wil zeggen dat op het oppervlak van de planeet ten tijde van het schot de som van de kinetische energie van de projectiel + zwaartekrachtenergie moet zijn, ongeldig zijn:

½ m ve^2 - (g m.Dhr_T = 0

Merk op dat de uitlaatsnelheid niet afhangt van het deeg van het projectiel en de vierkante waarde is

Ve^2 = (2g m) / r_T

Als de planeet instort tot een straal helft van het origineel wordt het vierkant van de nieuwe uitlaatsnelheid dubbel.

Daarom groeit de nieuwe uitlaatsnelheid en wordt 1.41 keer de oude ontsnappingssnelheid:

Ve '= 1.41 Zie

Oefening 3: Apple Gravitational Energy

Een jongen op het balkon van een gebouw op 30 meter van de grond brengt een appel van 250 g los, die na een paar seconden de grond bereikt.

Figuur 4. Tijdens het vallen wordt de potentiële energie van de appel omgezet in kinetische energie. Bron: Pixabay.

a) Wat is het verschil van zwaartekrachtenergie van de appel aan de bovenkant van de appel op grondniveau?

b) Hoe snel deed de appel net voordat hij zich op de grond verspreidde?

c) Hoe zit het met energie zodra de appel tegen de grond verpletterde? 

Oplossing

a) Het verschil in zwaartekrachtenergie is 

M.G.H = 0.250 kg * 9.81 m/s^2 * 30 m = 73.6 J

b) De potentiële energie die de appel had wanneer deze 30 m hoog was, wordt omgezet in kinetische energie voor wanneer de appel de grond bereikt.

½ m V^2 = m.G.H

V^2 = 2.G.H

Door waarden en opruiming te vervangen, volgt hieruit dat de appel de grond bereikt met een snelheid van 24.3 m/s = 87.3 km/h.

c) Het is duidelijk dat de appel verspreid is en alle in het begin op het begin is opgebouwd, is verloren in de vorm van warmte, omdat de appelstukken en de impactzone worden verwarmd, bovendien wordt een deel van de energie ook gedissipeerd in de vorm van geluidsgolven "Splash".

Referenties

1. Alonso, m. (1970). Vol -fysica. 1, Inter -American Educational Fund. 
2. Hewitt, Paul. 2012. Conceptuele fysieke wetenschap. 5e. ED. Pearson.
3. Ridder, r. 2017. Fysica voor wetenschappers en engineering: een strategiebenadering. Pearson.
4. Sears, f. (2009).University Physics Vol. 1 
5. Wikipedia. Zwaartekrachtenergie. Hersteld van: is.Wikipedia.com
6. Wikipedia. Zwaartekrachtenergie. Opgehaald uit: in.Wikipedia.com