Ellipsoïde kenmerken en voorbeelden

Hij ellipsoïde Het is een oppervlak in de ruimte die behoort tot de groep quadrische oppervlakken en waarvan de algemene vergelijking van de vorm is:

Bijl² + Door² + CZ² + Dxy + exz + fyz + gx + hy + iz + j = 0

Het is het drie -dimensionale equivalent van een ellips, gekenmerkt door elliptische en cirkelvormige sporen in sommige speciale gevallen. De sporen zijn de krommen die worden verkregen bij het kruisen van de ellipsoïde met een vlak.

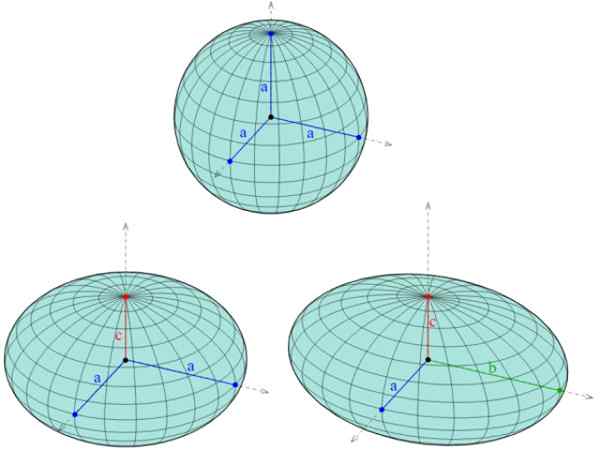
Figuur 1. Three different ellipsoids: above a sphere in which the three half -semi are the same, down to the left a spheroid, with two equal half -and -one semi -axis and finally down to the right, a triaxial spheroid, with three axes van verschillende lengte. Bron: Wikimedia Commons. AG2GAEH/CC BY-S (https: // creativeCommons.Org/licenties/by-sa/4.0)

Naast de ellipsoïde zijn er vijf andere quadric: hyperboloid van één blad en twee bladeren, twee soorten paraboloïde (hyperbolisch en elliptisch) en de elliptische kegel. Zijn sporen zijn ook conisch.

De ellipsoïde kan ook worden uitgedrukt door de standaardvergelijking in Cartesiaanse coördinaten. Een ellipsoïde was gericht op oorsprong (0,0,0) en op deze manier uitgedrukt, herinnert de ellips, maar met een extra term:

De waarden van naar, B En C Ze zijn reële getallen groter dan 0 en vertegenwoordigen de drie ellipsoïde helft.

[TOC]

Ellipsoïde kenmerken

- Standaardvergelijking 

De standaardvergelijking in Cartesiaanse coördinaten voor de ellips was gericht op het punt (H, K, M) is:

- Ellipsoïde parametrische vergelijkingen

In bolvormige coördinaten kan de ellipsoïde als volgt worden beschreven:

x = een sin θ. Cos φ

y = b sin θ. Sin φ

Z = c cos θ

De ellipsoïde semi -out zijn nog steeds a, b en c, terwijl de parameters de hoeken θ en φ van de volgende figuur zijn:

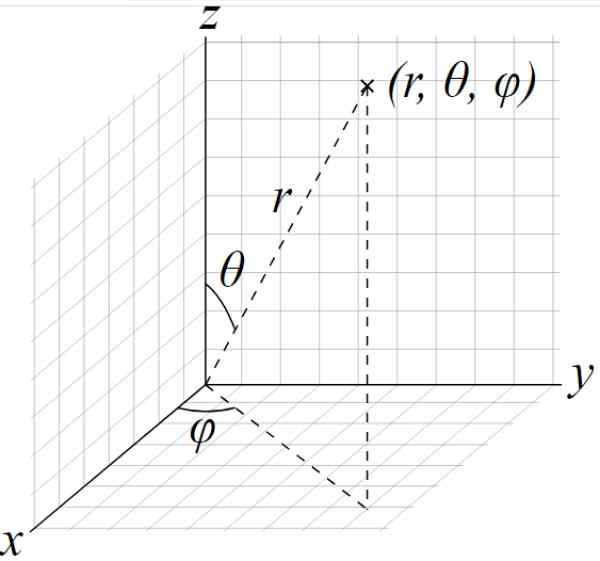Figuur 2. Het sferische coördinatensysteem. De ellipsoïde kan worden geparametreerd met behulp van de hoeken die theta en phi als parameters hebben getoond. Bron: Wikimedia Commons. Andeggs / pub -domein.

- Ellipsoïde sporen

De algemene vergelijking van een oppervlak in de ruimte is f (x, y, z) = 0 en de sporen van het oppervlak zijn de krommen:

Kan u van dienst zijn: vectorgrootte

- x = c; F (c, y, z) = 0

- y = c; F (x, c, z) = 0

- Z = c; F (x, y, c) = 0

In het geval van een ellipsoïde zijn dergelijke curven ellipsen en soms omtrek.

- Volume

Het deel V van de ellipsoïde wordt gegeven door (4/3) π maal het product van zijn drie half -semi:

V = (4/3) π. abc

Speciale ellipsoïde cases

-Een ellipsoïde wordt een bol wanneer alle helft -size dezelfde grootte heeft: a = b = c ≠ 0. Dit is logisch, omdat de ellipsoïde is als een bol waarnaar hij in elke as anders is uitgerekt.

-De sferoïde is een ellipsoïde waarin twee van de semijes identiek zijn en de derde anders is, bijvoorbeeld kan het a = b ≠ c zijn.

De sferoïde wordt ook revolutie ellipsoïde genoemd, omdat deze kan worden gegenereerd door ellipsen rond een as te roteren.

Als de draaias samenvalt met de hoofdas, is de sferoïde prolitie, Maar als het samenvalt met de kleine as, is het dat openbaar maken:

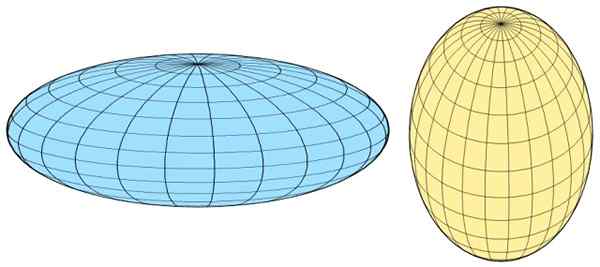figuur 3. Sferoïde links naar links en sferoïde prolitie rechts. Bron: Wikimedia Commons.

De maat voor de afvlakking van de sferoïde (ellipticiteit) wordt gegeven door het verschil in lengte tussen de twee semi -pagina's, uitgedrukt in een fractionele vorm, dat wil zeggen dat het de eenheid afvlakt, gegeven door:

F = (a - b) / a

In deze vergelijking vertegenwoordigt A de semi -senije en B de kleine semi -as, onthoud dat de derde as gelijk is aan een van deze voor een sferoïde. De waarde van F ligt tussen 0 en 1 en voor een sferoïde moet deze groter zijn dan 0 (als het gelijk was aan 0, zouden we gewoon een bol hebben).

Kan u van dienst zijn: Bethelgeuse

De referentie ellipsoïde

De planeten en in het algemeen zijn de sterren meestal geen perfecte bollen, omdat de rotatiebeweging rond hun bijlen het lichaam in de palen en bassinalen in Ecuador splitst.

Dat is de reden waarom de aarde blijkt te zijn als een Oblate Spheroid, hoewel niet zo overdreven als die van de vorige figuur, en aan de andere kant is de gasvormige Saturn Giant de meest bittere van de planeten in het zonnestelsel.

Dus een meer realistische manier om de planeten te vertegenwoordigen, is om aan te nemen dat ze zijn als een sferoïde of ellipsoïde van Revolution, wiens semi -semi -major de equatoriale radio is en de kleine semi -as de polaire straal.

Zorgvuldige maatregelen die op de wereld worden genomen, hebben de Referentie ellipsoïde van de aarde als zijn meest precieze vorm om wiskundig te werken.

De sterren hebben ook rotatiebewegingen die ze min of meer afgeplatte vormen geven. De snelle Aternar -ster, de achtste helderste ster in de nachtelijke hemel, in de zuidelijke constellatie van Eridanus is opmerkelijk elliptisch bij het vergelijken met de meerderheid. Het is 144 lichtjaren van ons.

Aan het andere uiterste, een paar jaar geleden gaven de wetenschappers met het meest sferische object dat tot nu toe werd gevonden: de Kepler 11145123 -ster, 5000 lichtjaren, met een grootte tweemaal die van onze zon en een verschil tussen de semi -gemontages van slechts 3 km. Zoals verwacht, wordt het ook langzamer.

Wat de aarde betreft, het is geen perfecte sferoïde vanwege het ruige oppervlak en de lokale variaties van de zwaartekracht. Daarom is er meer dan één beschikbare referentie -sferoïde en op elke site wordt de meest geschikt voor lokale geografie gekozen.

Het kan je van dienst zijn: wat is de vallei in de natuurkunde? (Met voorbeelden)

De hulp van de satellieten is van onschatbare waarde bij het creëren van meer precieze modellen van de vorm van de aarde, dankzij hen is het bijvoorbeeld bekend dat de Zuidpool dichter bij Ecuador is dan de Noordpool.

Figuur 4. Haumea, de TransNeptunian Dwarf Planet heeft een ellipsvormige vorm. Bron: Wikimedia Commons.

Numeriek voorbeeld

Vanwege de rotatie van de aarde wordt een centrifugale kracht gegenereerd die het de vorm geeft van een langwerpige ellipsoïde, in plaats van een bol. Het is bekend dat de equatoriale radio van de aarde 3963 mijl is en de polaire straal 3942 mijl is.

Zoek de vergelijking van het equatoriale spoor, die van deze ellipsoïde en de maat voor zijn afvlakking. Vergelijk ook met de ellipticiteit van Saturnus, met de onderstaande gegevens:

-Saturn Equatorial Radio: 60268 km

-Saturn Polar Radio: 54364 km

Oplossing

Een coördinatensysteem is vereist, dat we zullen aannemen dat gericht is op de oorsprong (centrum van de aarde). We gaan ervan uit dat de verticale Z -as en het spoor dat overeenkomt met de evenaar op het XY -vlak, gelijkwaardig aan het vlak Z = 0 bevindt.

In het equatoriale vlak zijn de semi -A en B hetzelfde, daarom a = b = 3963 mijl, terwijl c = 3942 mijl. Dit is een speciaal geval: een sferoïde gericht op het punt (0.0.0) zoals hierboven vermeld.

Het equatoriale spoor is een cirkel van straal r = 3963 mijl, gericht op de oorsprong. Het wordt berekend door Z = 0 te doen in de standaardvergelijking:

En de standaardvergelijking van de ellipsoïde van de aarde is:

Ten slotte wordt de aanpassingsmaatregel (elliptisch) berekend in de vergelijking evalueren:

F _Land = (a - b) / a = (3963-3942) mijlen / 3963 mijl = 0.0053

F _Saturnus = (60268-54363) km/60268 km = 0.0980

Merk op dat elliptische F een dimensieloze hoeveelheid is.

Referenties

1. Arcgis voor desktop. Sferoïde en bollen. Hersteld van: desktop.Arcgis.com.
2. BBC World. Het mysterie van het meest sferische object ooit ontdekt in het universum. Opgehaald uit: BBC.com.
3. Larson, r. Berekening en analytische geometrie. Zesde editie. Deel 2. McGraw Hill.
4. Wikipedia. Ellipsooid. Opgehaald uit: in.Wikipedia.borg.
5. Wikipedia. Siperoïde. Opgehaald uit: in.Wikipedia.borg.