Polynoomvergelijkingen

Wat zijn polynoomvergelijkingen?

De Polynoomvergelijkingen Ze zijn een verklaring die de gelijkheid van twee uitdrukkingen of leden verhoogt, waarbij ten minste een van de voorwaarden die aan elke kant van gelijkheid vormen polynomen P (x). Deze vergelijkingen worden genoemd volgens de mate van hun variabelen.

Over het algemeen is een vergelijking een verklaring die de gelijkheid van twee uitdrukkingen vaststelt, waarbij er in ten minste een van deze onbekende hoeveelheden zijn, die variabelen of onbekenden worden genoemd. Hoewel er veel soorten vergelijkingen zijn, worden deze over het algemeen in twee soorten ingedeeld: algebraïsch en transcendent.

Polynoomvergelijkingen bevatten alleen algebraïsche uitdrukkingen, die een of meer onbekenden kunnen hebben die tussenbeide komen in de vergelijking. Volgens de exponent (graad) die ze hebben, kunnen ze worden geclassificeerd als: Eerste leerjaar (lineair), tweede klas (kwadratisch), derde leerjaar (kubiek), vierde leerjaar (quantic), van graad groter dan of gelijk aan vijf en irrationeel.

Kenmerken van polynoomvergelijkingen

Polynoomvergelijkingen zijn uitdrukkingen die worden gevormd door een gelijkheid tussen twee polynomen; Dat wil zeggen, voor de eindige bedragen van vermenigvuldiging tussen waarden die onbekend zijn (variabelen) en vaste getallen (coëfficiënten), waarbij de variabelen exponenten kunnen hebben, en hun waarde een positief geheel getal kan zijn, inclusief nul.

Exponenten bepalen de graad of het type vergelijking. Die term van de uitdrukking die de meeste waarde -exponent heeft, zal de absolute mate van polynoom vertegenwoordigen.

Polynoomvergelijkingen worden ook wel algebraïsch genoemd, hun coëfficiënten kunnen reële of complexe getallen zijn en de variabelen zijn onbekende getallen die worden weergegeven door een letter, zoals: "x".

Als door een waarde te vervangen door de variabele "x" in p (x), is het resultaat gelijk aan nul (0), dan wordt gezegd dat deze waarde voldoet aan de vergelijking (het is een oplossing) en wordt het algemeen de polynoomwortel genoemd.

Wanneer een polynoomvergelijking wordt ontwikkeld, willen alle wortels of oplossingen worden gevonden.

Soorten polynoomvergelijkingen

Er zijn verschillende soorten polynoomvergelijkingen, die worden onderscheiden volgens het aantal variabelen, en ook volgens hun mate van exponent.

De polynoomvergelijkingen -waar de eerste termijn een polynoom is die slechts één onbekend heeft, gezien het feit dat de graad elk natuurlijk getal (n) kan zijn en de tweede term is nul -kan als volgt worden uitgedrukt:

Kan u van dienst zijn: geschiedenis van trigonometrie van de oorsprong ervan

naar_{N *} X^N + naar_{N-1 *} X^N-1 +… + A_{1 *} X¹ + naar_{0 *} X₀ = 0

Waar:

• naar_N, naar_N-1 al₀, Het zijn echte coëfficiënten (cijfers).
• naar_N verschilt van nul.
• Exponent n is een positief geheel getal dat de mate van vergelijking vertegenwoordigt.
• x is de variabele of onbekende die moet worden gezocht.

De absolute of grotere mate van een polynoomvergelijking is dat exponent van grotere waarde onder allen die polynoom vormen; Op deze manier worden vergelijkingen geclassificeerd als:

Eerste leerjaar

De eerste graad polynoomvergelijkingen, ook bekend als lineaire vergelijkingen, zijn die waaraan de graad (de grootste exponent) gelijk is aan 1, de polynoom is van de vorm P (x) = 0; En het bestaat uit een lineaire en een onafhankelijke term. Het is als volgt geschreven:

Ax + B = 0.

Waar:

• A en B zijn reële getallen en a ≠ 0.
• Bijl is de lineaire term.
• B is de onafhankelijke termijn.

Bijvoorbeeld, vergelijking 13x - 18 = 4x.

Om lineaire vergelijkingen op te lossen, moeten alle termen die de onbekende X bevatten aan de kant van gelijkheid worden doorgegeven, en degenen die niet aan de andere kant bewegen, om het te wissen en een oplossing te verkrijgen:

13x - 18 = 4x

13x = 4x + 18

13x - 4x = 18

9x = 18

x = 18 ÷ 9

x = 2.

Op deze manier heeft de gegeven vergelijking slechts één oplossing of root, wat x = 2 is.

Tweede leerjaar

De tweede graad polynomiale vergelijkingen, ook bekend als kwadratische vergelijkingen, zijn die waarin de graad (de grootste exponent) gelijk is aan 2, de polynoom is van de vorm P (x) = 0 en is samengesteld uit een kwadratische term, een lineair en een onafhankelijke. Het wordt als volgt uitgedrukt:

bijl² + bx + c = 0.

Waar:

• A, B en C zijn reële getallen en a ≠ 0.
• bijl² Het is de kwadratische term, en "a" is de coëfficiënt van de kwadratische term.
• BX is de lineaire term, en "B" is de coëfficiënt van de lineaire term.
• C is de onafhankelijke termijn.

Oplossen

Over het algemeen wordt de oplossing voor dit type vergelijkingen gegeven bij het opruimen van X van de vergelijking, en blijft als volgt, wat een resolvent wordt genoemd:

Kan u van dienst zijn: binomiale stelling

Daar, (b² - 4ac) wordt discriminerend uit de vergelijking genoemd en deze uitdrukking bepaalt het aantal oplossingen dat de vergelijking kan hebben:

• Ja b² - 4ac) = 0, de vergelijking heeft een enkele oplossing die dubbel is; dat wil zeggen, het zal twee gelijke oplossingen hebben.
• Ja b² - 4ac)> 0, de vergelijking zal twee verschillende echte oplossingen hebben.
• Ja b² - 4ac) < 0, la ecuación no tiene solución (tendrá dos soluciones complejas distintas).

U hebt bijvoorbeeld de 4x -vergelijking² + 10x - 6 = 0, om het eerst op te lossen, worden de termen A, B en C geïdentificeerd en vervolgens wordt het vervangen in de formule:

A = 4

B = 10

C = -6.

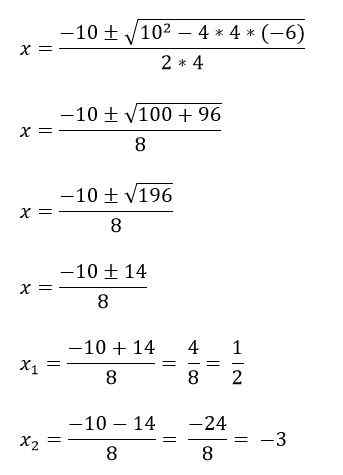
Er zijn gevallen waarin de tweede -grade -aftroffolynoomvergelijkingen niet de drie termen hebben, en daarom zijn ze anders opgelost:

• In het geval dat kwadratische vergelijkingen niet de lineaire term hebben (dat wil zeggen B = 0), wordt de vergelijking uitgedrukt als bijl² + C = 0. Om het op te lossen, wordt X gewist² En de vierkante wortels worden in elk lid toegepast en onthouden dat de twee mogelijke tekenen die het onbekende mogelijk heeft:

bijl² + C = 0.

X² = - C ÷ A

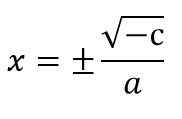
Bijvoorbeeld 5 x² - 20 = 0.

5 x² = 20

X² = 20 ÷ 5

x = ± √4

x = ± 2

X₁ = 2.

X₂ = -2.

• Wanneer de kwadratische vergelijking geen onafhankelijke term heeft (dat wil zeggen c = 0), wordt de vergelijking uitgedrukt als bijl² + Bx = 0. Om het op te lossen, moet de gemeenschappelijke factor van de onbekende X in het eerste lid worden genomen; Aangezien de vergelijking is gekoppeld aan nul, wordt vervuld dat ten minste een van de factoren gelijk zal zijn aan 0:

bijl² + Bx = 0.

x (ax + b) = 0.

Op deze manier moet je:

x = 0.

x = -b ÷ a.

Bijvoorbeeld: u heeft vergelijking 5x² + 30x = 0. Ten eerste is het factor:

5x² + 30x = 0

x (5x + 30) = 0.

Er worden twee factoren gegenereerd die x y zijn (5x + 30). Een van deze zal als nul worden beschouwd en de andere krijgt een oplossing:

X₁ = 0.

5x + 30 = 0

5x = -30

x = -30 ÷ 5

X₂ = -6.

Hoogste cijfer

De belangrijkste mate polynoomvergelijkingen zijn die die variëren van de derde klas, die kunnen worden uitgedrukt of opgelost met de algemene polynoomvergelijking voor elke mate:

Kan u van dienst zijn: Correlatiecoëfficiënt: formules, berekening, interpretatie, voorbeeld

naar_{N *} X^N + naar_{N-1 *} X^N-1 +… + A_{1 *} X¹ + naar_{0 *} X₀ = 0

Dit wordt gebruikt omdat een vergelijking met een graad groter dan twee het resultaat is van de factorisatie van een polynoom; dat wil zeggen, het wordt uitgedrukt als de vermenigvuldiging van graad één of grotere polynomen, maar zonder echte wortels.

De oplossing van dit type vergelijkingen is direct, omdat de vermenigvuldiging van twee factoren gelijk zal zijn aan nul als een van de factoren nul is (0); Daarom moet elk van de gevonden polynoomvergelijkingen worden opgelost, waarbij elk van zijn factoren overeenkomt met nul.

U hebt bijvoorbeeld de derde graad vergelijking (kubus) x³ + X² +4x + 4 = 0. Om het op te lossen, moet u de volgende stappen volgen:

• De voorwaarden zijn gegroepeerd:

X³ + X² +4x + 4 = 0

(X³ + X² ) + (4x + 4) = 0.

• Leden gaan af om de gemeenschappelijke factor van het onbekende te krijgen:

X² (x + 1) + 4 (x + 1) = 0

(X² + 4)_*(x + 1) = 0.

• Op deze manier worden twee factoren verkregen, die gelijk moeten zijn aan nul:

(X² + 4) = 0

(x + 1) = 0.

• Het is te zien dat de factor (x² + 4) = 0 heeft geen echte oplossing, terwijl de factor (x + 1) = 0 ja. Daarom is de oplossing:

(x + 1) = 0

x = -1.

Opgeloste oefeningen

Los de volgende vergelijkingen op:

Eerste oefening

(2x² + 5)_*(X - 3)_*(1 + x) = 0.

Oplossing

In dit geval wordt de vergelijking uitgedrukt als de vermenigvuldiging van polynomen; dat wil zeggen, het is gefactoriseerd. Om het op te lossen, moet elke factor gelijk zijn aan nul:

2x² + 5 = 0, heeft geen oplossing.

X - 3 = 0

X = 3.

1 + x = 0

x = - 1.

Op deze manier heeft de gegeven vergelijking twee oplossingen: x = 3 en x = -1.

Tweede oefening

X⁴ - 36 = 0.

Oplossing

Er werd een polynoom gegeven, die kan worden ingeschreven als een verschil in vierkanten om een ​​snellere oplossing te bereiken. De vergelijking blijft dus:

(X² + 6)_*(X² - 6) = 0.

Om de oplossing van de vergelijkingen te vinden, zijn beide factoren gelijk aan nul:

(X² + 6) = 0, heeft geen oplossing.

(X² - 6) = 0

X² = 6

x = ± √6.

De eerste vergelijking heeft dus twee oplossingen:

x = √6.

x = - √6.