Fractionele vergelijkingen
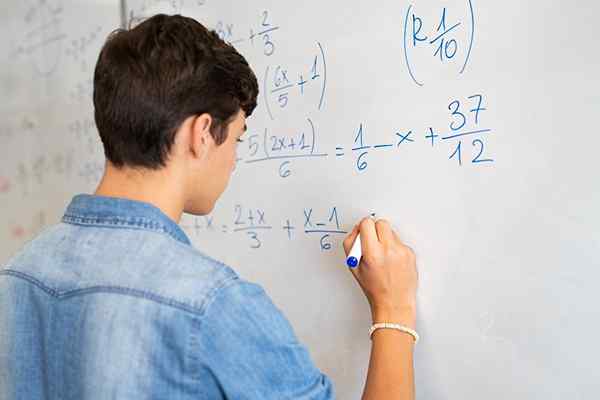
- 4912
- 861
- Dr. Rickey Hudson
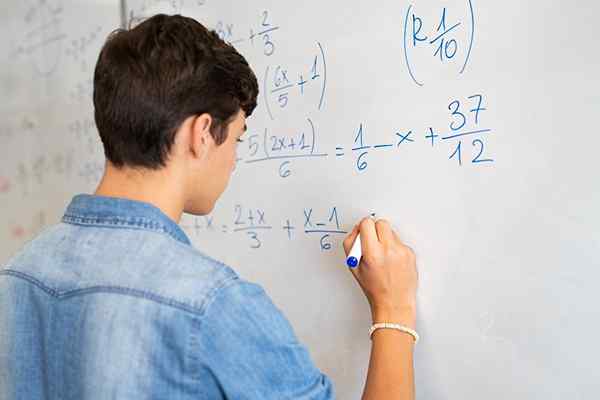 Fractionele vergelijkingen omvatten numerieke en/of algebraïsche fracties, en het onbekende kan zowel in de teller als in de noemer zijn, of beide
Fractionele vergelijkingen omvatten numerieke en/of algebraïsche fracties, en het onbekende kan zowel in de teller als in de noemer zijn, of beide Wat zijn fractionele vergelijkingen?
De fractionele vergelijkingen zijn die die breuken bevatten in een of meer van hun voorwaarden. Dergelijke breuken kunnen numeriek of algebraïsch zijn, waarbij het onbekende kan worden gevonden in de teller en/of in de noemer van een termijn.
Vervolgens enkele voorbeelden van fractionele vergelijkingen met een enkele onbekende:
Het eerste voorbeeld is een lineaire vergelijking met fractionele coëfficiënten; In het tweede voorbeeld bevindt het onbekende zich in de noemer van elk van de termen, en in de laatste is het onbekende zowel de teller als in de noemer.
Om ze op te lossen, is het noodzakelijk om enkele algebraïsche transformaties uit te voeren en dus een equivalente vergelijking te verkrijgen, waarin het onbekende niet in de noemer verschijnt. Nadat deze procedure is uitgevoerd, wordt de oplossing gevonden met behulp van de juiste technieken.
De oplossing bestaat uit de set van "x" waarden die voldoen aan gelijkheid. Het kan een unieke waarde zijn, of meerdere, maar in ieder geval is het erg belangrijk om te onthouden dat niet alle oplossingen in de equivalente vergelijking acceptabel zijn voor de oorspronkelijke vergelijking.
Inderdaad, als het een vergelijking is waarvan de onbekende zich in de noemer bevindt, moeten de "x" -waarden die deze worden vermeden, zelfs als ze behoren tot de set equivalente vergelijkingsoplossingen. Dit komt omdat de verdeling tussen 0 niet is gedefinieerd.
Als de equivalente vergelijking een unieke oplossing heeft en blijkt dat de noemer van een van de voorwaarden van de oorspronkelijke vergelijking wordt geannuleerd, dan heeft deze geen oplossing.
Hoe een fractionele vergelijking op te lossen
De bewerkingen die worden uitgevoerd om niet -fractionele vergelijkingen op te lossen, zijn geldig, op voorwaarde dat gelijkheid wordt gehandhaafd. Op deze manier kunt u in een fractionele vergelijking dezelfde hoeveelheid toevoegen of aftrekken aan beide zijden van gelijkheid, alle termen met dezelfde hoeveelheid vermenigvuldigen of elke term delen met dezelfde hoeveelheid (verschillend van 0).
Kan u van dienst zijn: Bolzano StellingMaar omdat de fractionele vergelijking nodig is om te transformeren in een ander equivalent zonder noemers, worden de volgende algemene indicaties ook gevolgd:
- Zoek het minimale gemeenschappelijke veelvoud van noemers (m.C.M).
- Vermenigvuldig elke term met de M.C.M., Om denominators te elimineren.
- Los de verkregen equivalente vergelijking op.
- Controleer of de gevonden oplossingen voldoen aan de oorspronkelijke gelijkheid.
Soorten equivalente vergelijkingen
De equivalente vergelijkingen verkregen volgens de aangegeven procedure kunnen zijn:
- Lineair of eerste graad
- Kwadratisch
- Van hogere orde
Opgeloste voorbeelden
voorbeeld 1
Los de volgende vergelijking op:
Opgemerkt wordt dat de vergelijking eerste graad is in "X", omdat "X" hoog is op 1. De coëfficiënten van de vergelijking zijn breuken en een manier om ze te elimineren, om met hele getallen te werken, het vermenigvuldigt alle voorwaarden met het minimale veelvoud van noemers (m.C.M.)).
M.C.M. (2,3,6) = 6
Dus:
3x - 2x = 1
x = 1
De lezer kan de geldigheid van deze oplossing controleren, x = 1 vervangen in de oorspronkelijke vergelijking en verifiëren dat een gelijkheid wordt verkregen.
Voorbeeld 2
Bepaal de "x" -waarden die voldoen:
In tegenstelling tot het vorige voorbeeld is het onbekende in dit geval te vinden in de noemer. Merk op dat de noemers zijn geannuleerd voor de waarden x = 2 en x = −1, een detail dat handig is om rekening te houden, omdat, als de equivalente vergelijking deze oplossingen toelaat, we ze moeten weggooien, omdat ze niet toelaatbaar zijn In de oorspronkelijke vergelijking.
Nu moeten we de vergelijking omzetten in een andere zonder noemers, de eerste stap is om de som van termen links van gelijkheid te maken:
Aangezien de noemers hetzelfde zijn, zodat gelijkheid wordt vervuld, is het noodzakelijk dat de tellers ook zijn:
Kan u van dienst zijn: evenredigheid Constant: wat is, berekening, oefeningen4 (x+1) - 3 (x -2) = 8
Het is voldoende om deze vergelijking op te lossen, die het eerste leerjaar blijkt te zijn:
4x + 4 - 3x + 6 = 8
x = 8 - 6 - 4 = - 2
x = - 2
Omdat deze waarde verschilt van de verboden waarden, wordt deze toegelaten als een oplossing van de oorspronkelijke vergelijking.
Voorbeeld 3
Vind de oplossing van:
In deze vergelijking annuleert de waarde X = 4 de noemers, daarom is deze uitgesloten van de oplossingset van de getransformeerde vergelijking, als deze verscheen.
De getransformeerde vergelijking is gemakkelijk te vinden, het is voldoende om alle termen te vermenigvuldigen met de factor (x-4):
Verblijven:
2x - 4 = 4
2x = 8
x = 4
Voorbeeld 4
Los De vergelijking op:
In dit geval hebben noemers kwadratische termen, dus het is handig om ze eerst te laten factureren:
- X2 + 8x + 7 = (x + 7) (x + 1)
- X2 - 49 = (x + 7) (x - 7)
- X2 - 6x - 7 = (x - 7) (x + 1)
De vergelijking is als volgt:
De waarden van x die een van de noemers annuleren zijn: x = −7, x = 7, x = −1. Daarom, zelfs als deze waarden deel uitmaken van de oplossingsset van de gemodificeerde vergelijking, kunnen ze geen oplossing zijn van de oorspronkelijke vergelijking.
Nu komt het proces van het transformeren van de vergelijking. De eerste stap is om het minimale gewone veelvoud van noemers te vinden:
M.C.M. = (x + 7) (x - 7) (x + 1)
Door zich te vermenigvuldigen aan beide zijden van gelijkheid door M.C.M. is overgebleven:
Resulterend:
(x --7) (x− 2) = (x + 1) (2x - 5) - (x + 7) (x - 2)
Via distributive eigendom worden de producten ontwikkeld:
X2 - 9x +14 = 2x2 - 3x - 5 - (x2 + 5x - 14)
Vergelijkbare termen aan de rechterkant verminderen:
X2 - 9x + 14 = x2 - 8x + 9
De kwadratische voorwaarden worden geannuleerd door hetzelfde teken te voldoen aan verschillende kanten van gelijkheid:
Kan u van dienst zijn: Cubes Differention: Formules, Vergelijkingen, Voorbeelden, oefeningen- 9x + 14 = - 8x + 9
-x = -5 ⇒ x = 5
Dit resultaat wordt toegelaten als een oplossing, omdat het geen van de verboden waarden is.
Toepassing uitoefening van fractionele vergelijkingen
De noemer van een fractie overschrijdt vier eenheden voor de teller. Als de teller wordt afgetrokken van de teller en de noemer ook, is de resulterende fractie 3/5. Bepaal de oorspronkelijke fractie.
Oplossing
Laat X de waarde van de teller zijn.
Aangezien de fractie -noemer vier eenheden van de teller overschrijdt, is de oorspronkelijke fractie:
Nu moet u 5 eenheden aftrekken, zowel aan de teller als aan de noemer:
Aangezien de breuk die voortvloeit uit het uitvoeren van de vorige procedure gelijk is aan 3/5, worden ze gelijkgesteld:
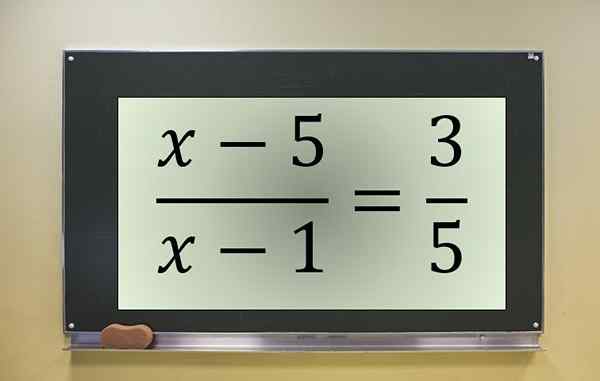 Fractionele vergelijking voorbeeld. Bron: f. Zapata.
Fractionele vergelijking voorbeeld. Bron: f. Zapata. Dit is een fractionele vergelijking met het onbekende in teller en noemer, die wordt geannuleerd op x = 1. Daarom moet deze waarde worden uitgesloten, als het een van de oplossingen van de getransformeerde vergelijking was.
Vervolgens vermenigvuldigt het beide zijden met het minimale gewone veelvoud, dat is 5 (x - 1):
Resulterend in de volgende equivalente vergelijking:
5 (x - 5) = 3 (x - 1)
Distributieve onroerend goed toepassen:
5x -25 = 3x - 3 ⇒ 2x = 22
X = 11
De oorspronkelijke fractie vervangt x = 11 in de uitdrukking:
Resulterend in fractie 11/15. Dit is het antwoord op het probleem.
Referenties
- Fractionele vergelijkingen. Hersteld van: Mathepower.com
- Wiskundeportaal. Fractionele vergelijkingen. Probleem oplossing. Hersteld van: silvioduarte.com.
- Stewart, J. (2007). Precculment: wiskunde voor berekening. 5e. Editie. Cengage leren.
- Sullivan, m. (1997). Voorzetting. 4e. Editie. Pearson Education.
- Zill, D. (2008). Voorrang op berekening vooruitgang. 4e. Editie. McGraw Hill.



(x+1))

=6\left%20(%20\frac16%20\right%20))
-3(x-2)(x-2)(x+1)=\frac8(x-2)(x+1))
\left%20(%20\fracxx-4%20\right%20)+(x-4)=(x-4)\left%20(%20\frac4x-4%20\right%20))

(x+1)=\frac2x-5(x+7)(x-7)-\fracx-2(x-7)(x+1))
(x-7)(x+1)\left%20[%20\fracx-2(x+7)(x+1)%20\right%20]=(x+7)(x-7)(x+1)\left%20[%20\frac2x-5(x+7)(x-7)-\fracx-2(x-7)(x+1)%20\right%20])



\left%20(%20\fracx-5x-1%20\right%20)=5(x-1)\frac35)