Tweede graad vergelijkingen formule, hoe ze op te lossen, voorbeelden, oefeningen
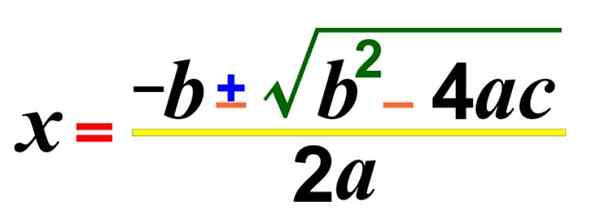
- 4846
- 790
- Dr. Rickey Hudson
De Tweede graad of kwadratische vergelijkingen En een onbekende heeft de vorm bijl2 + bx + c = 0. Waarbij a ≠ 0, sinds het is, de vergelijking zou worden omgezet in een lineaire vergelijking, en coëfficiënten A, B en C zijn reële getallen.
Het te bepalen onbekende is de waarde van x. Bijvoorbeeld de 3x -vergelijking2 - 5x + 2 = 0 is een complete tweede graad vergelijking.
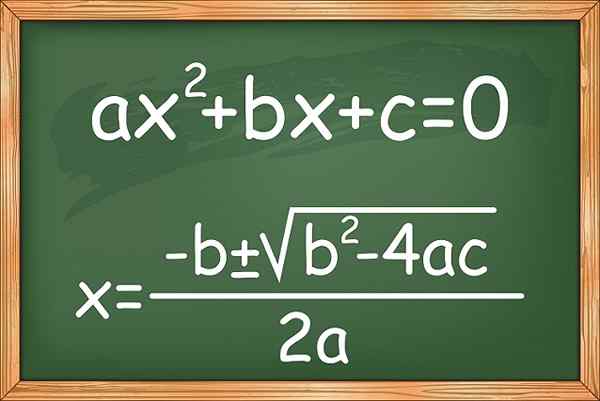 Figuur 1. De formule voor het oplossen van tweede graad of kwadratische vergelijkingen van een onbekende
Figuur 1. De formule voor het oplossen van tweede graad of kwadratische vergelijkingen van een onbekende Er zijn ook varianten die bekend staan als onvolledige tweede -graden vergelijkingen, die geen van de voorwaarden missen, behalve die van bijl2. Hier zijn enkele voorbeelden:
X2 - 25 = 0
3x2 - 5x = 0
Al Juarismi, de beroemde Arabische wiskundige van de oudheid, beschreef in zijn werken verschillende soorten eerste en tweede graad vergelijkingen, maar alleen met positieve coëfficiënten. Het was echter de Franse wiskundige Oplossen:
Dit is een algemene formule die het mogelijk maakt om een kwadratische vergelijking op te lossen, de wortels of nullen van hetzelfde te vinden, zelfs als de oplossingen niet echt zijn. Er zijn ook andere manieren om ze op te lossen.
[TOC]
Hoe u de tweede klas vergelijkingen oplossen?
Tweede -gradenvergelijkingen kunnen worden opgelost door de hierboven gegeven formule, en er zijn ook andere algebraïsche procedures die in sommige vergelijkingen kunnen werken.
We gaan de voorgestelde vergelijking in het begin oplossen met de formule, een geldige methode voor elke tweede graad vergelijking met een onbekenden:
3x2 - 5x + 2 = 0
Om de formule te gebruiken, merken we terecht op dat:
- naar Het is de coëfficiënt van de term met x2
- B Het is de coëfficiënt van de lineaire term
- C is de onafhankelijke termijn.
Laten we ze uit dezelfde vergelijking identificeren:
A = 3
B = -5
C = 2
Merk op dat het teken dat bij de coëfficiënt hoort, moet worden gehouden. Nu vervangen we deze waarden in de formule:
In de teller is het symbool van "meer - minder" ±, wat aangeeft dat de hoeveelheid met wortel als positief en ook als negatief kan worden beschouwd. Een tweede graadvergelijking heeft maximaal twee echte oplossingen, en dit symbool houdt er rekening mee.
Laten we X bellen1 en x2 Naar deze twee oplossingen, dan:
X1 = (5+1) / 6 = 1
X2 = (5-1)/6 = 4/6 = 2/3
Resolutie door factorisatie
Sommige tweede graad vergelijkingen bestaan uit trinomials die gemakkelijk factor zijn. Als dat zo is, is deze methode veel sneller. Overweeg de vergelijking:
X2 + 7x - 18 = 0
Factorisatie heeft deze vorm:
Kan u van dienst zijn: congruentie: congruente cijfers, criteria, voorbeelden, oefeningen(x +) ⋅ (x -)
De lege ruimtes zijn gevuld met twee nummers die, wanneer vermenigvuldigd in 18, en wanneer ze worden afgetrokken, 7 zijn 7. De tekenen tussen haakjes worden gekozen met dit criterium:
-In de eerste haakjes wordt het teken tussen de eerste en de tweede term geplaatst.
-En in de tweede haakjes gaat het product van de borden die worden gezien.
Wat de cijfers betreft, ze zijn gemakkelijk in dit geval: ze zijn 9 en 2. De oudste wordt altijd in de eerste van de haakjes geplaatst, zoals deze:
X2 + 7x - 18 = (x + 9). (x - 2)
De lezer kan controleren via distributieve eigenschap, die bij het ontwikkelen van het product van de rechterkant van gelijkheid, het trinomiaal van links wordt verkregen. Nu wordt de vergelijking herschreven:
(x + 9) ⋅ (x - 2) = 0
Om gelijkheid te vervullen, is het voldoende om een van de twee factoren nul te zijn. Dus, in de eerste moet het worden gedaan1 = -9 of het kan zijn dat de tweede factor is geannuleerd, in dat geval x2 = 2. Dit zijn de vergelijkingsoplossingen.
Grafische methode
De wortels of oplossingen van de tweede graadvergelijking komen overeen met de kruispunten van de gelijkenis y = = = bijl2 + bx + c Met de horizontale as of x -as. Zodat we door de overeenkomstige gelijkenis te leiden, de oplossing van de tweede graad vergelijking zullen vinden die y = 0 doet.
De sneden van de gelijkenissen met de horizontale as vertegenwoordigen de oplossingen van de vergelijking bijl2 + bx + c = 0. Een gelijkenis die slechts de horizontale as op een enkel punt snijdt, heeft een enkele wortel en dit zal altijd het hoekpunt van de parabool zijn.
En ten slotte, als een gelijkenis niet naar de horizontale as snijdt, de overeenkomstige vergelijking bijl2 + bx + c = 0 Het mist echte oplossingen.
Het bouwen van een handgrafiek kan moeizaam zijn, maar met het gebruik van programma's die online grafiek zijn, is het heel eenvoudig.
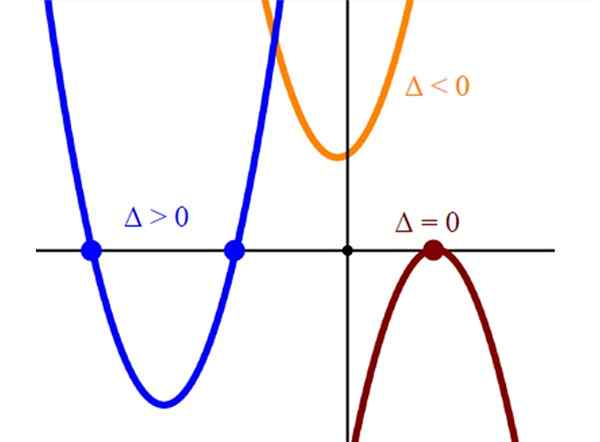 Figuur 2. Grafische weergave van drie soorten gelijkenissen, met twee, één en geen kruising met de horizontale as. Bron: Wikimedia Commons.
Figuur 2. Grafische weergave van drie soorten gelijkenissen, met twee, één en geen kruising met de horizontale as. Bron: Wikimedia Commons. Resolutie met wetenschappelijke rekenmachine
Veel modellen van wetenschappelijke rekenmachines hebben de mogelijkheid om tweede graad vergelijkingen op te lossen (en ook andere soorten vergelijkingen). Om het te weten, moet u het menu bekijken.
Zodra de kwadratische vergelijkingsoptie van een onbekend wordt gekozen, vraagt het menu om de waarden van coëfficiënten A, B en C in te voeren en de echte oplossingen terug te sturen als ze bestaan. En er zijn ook modellen van wetenschappelijke rekenmachines die met complexe nummers werken en deze oplossingen aanbieden.
Kan u van dienst zijn: veelvouden van 2: wat zijn en uitlegDiscrimineren van een tweede graad vergelijking
Om te weten of de vergelijking echte oplossingen heeft of niet, en hoeveel zijn, zonder de noodzaak om eerst op te lossen, wordt de discriminant gedefinieerd als de hoeveelheid onder de vierkantswortel:
Δ = B2 - 4AC
Volgens het discriminerende teken is het bekend hoeveel oplossingen de vergelijking heeft volgens dit criterium:
-Twee echte oplossingen: δ> 0
-Een echte oplossing (of twee identieke oplossingen): Δ = 0
-Geen echte oplossing: δ < 0
Hoeveel oplossingen hebben bijvoorbeeld de tweede graad -vergelijking -7x2 +12x + 64 = 0? We identificeren de coëfficiënten:
A = -7
B = 12
C = 64
Δ = B2 - 4AC = 122 - 4x (-7) x 64 = 144 + 1792 = 1936> 0
De vergelijking heeft twee oplossingen. Laten we nu eens kijken:
X2 - 6x + 9 = 0
A = 1
B = -6
C = 9
Δ = (-6)2 - 4 x 1 x 9 = 36 - 36 = 0
Dit is een vergelijking met een unieke oplossing of twee gelijke oplossingen.
Voorbeelden van eenvoudige tweedegraads vergelijkingen
In het begin zeiden we dat de tweede graadvergelijkingen compleet kunnen zijn als de trinomiale is, en onvolledig als de lineaire term of de onafhankelijke term ontbrak. Laten we nu enkele specifieke typen bekijken:
X vormvergelijking2 + mx + n = 0
In dit geval a = 1 en de formule wordt gereduceerd tot:
Voor dit type vergelijking, en altijd afhankelijk van de resterende coëfficiënten, kan de factorisatiemethode goed werken, zoals we in de voorgaande sectie zagen.
Onvolledige vergelijking van de bijlvorm2 + C = 0
De oplossing, als het bestaat, is de vorm:
Er is een echte oplossing wanneer A O C een negatief teken heeft, maar als de twee termen hetzelfde teken hebben, is de oplossing denkbeeldig.
Onvolledige vergelijking van de bijlvorm2 + Bx = 0
Deze vergelijking wordt snel opgelost door factorisatie te gebruiken, omdat de X een gemeenschappelijke factor is in beide termen. Een van de oplossingen is altijd x = 0, de andere is als volgt:
bijl2 + Bx = 0
x (ax + b) = 0
Ax + B = 0 → X = -b/A
Laten we dan naar een voorbeeld kijken. Oplossen:
X2 - 5x = 0
x (x - 5) = 0
Daarom x1 = 0 en x2 = 5
Vergelijkingen met noemer
Er zijn verschillende rationele vergelijkingen, waarin het onbekende zowel in de teller als in de noemer kan aanwezig zijn, of zelfs alleen in het laatste, en dat door algebraïsche manipulaties worden gereduceerd tot kwadratische vergelijkingen.
De manier om ze op te lossen, is om beide zijden van gelijkheid te vermenigvuldigen met de minimale gemeenschappelijke multiple of m.C.m van de noemers en herschikken vervolgens de voorwaarden. Bijvoorbeeld:
Kan u van dienst zijn: hoeveel diameters heeft een omtrek?Hogere orde vergelijkingen die worden omgezet in kwadratisch
Er zijn vergelijkingen van hogere orde die, door een variabele verandering, kunnen worden opgelost alsof ze kwadratisch zijn, bijvoorbeeld deze vergelijking Bicadrada:
X4 - 10x2 + 9 = 0
Laat x2 = U, dan wordt de vergelijking omgezet in:
of2 - 10U + 9 = 0
Deze vergelijking wordt snel opgelost door factorisatie, het vinden van twee getallen die zich in 9 vermenigvuldigen en 10 hebben toegevoegd. Deze cijfers zijn 9 en 1:
(U - 9).(U - 1) = 0
Daarom zijn de oplossingen van deze vergelijking u1 = 9 en u2 = 1. Nu geven we de verandering terug:
X2 = 9 → x1 = 3 en x2 = -3
X2 = 1 → x1 = 1 en x2 = -1
De oorspronkelijke vergelijking is van orde 4, daarom heeft het minstens 4 wortels. Het voorbeeld is -3, -1, 1 en 3.
Eenvoudige opgeloste oefeningen
- Oefening 1
Los de volgende kwadratische vergelijking op met het onbekende in de noemer:
Het minimale gewone multiple is x (x+2) en moet zich vermenigvuldigen met alle termen:
De equivalente uitdrukking blijft:
5x (x+2) - x = x (x+2)
We ontwikkelen:
5x2 + 10x - x = x2 + 2x
Alle termen worden links van gelijkheid omgezet en rechts is links 0:
5x2 + 10x - x - x2 - 2x = 0
4x2 - 7x = 0
We factoren, omdat het een onvolledige vergelijking is:
x (4x - 7) = 0
Een van de oplossingen is x = 0, de andere is:
4x = 7
x = 7/4
- Oefening 2
Vind de oplossing van de tweede graad vergelijkingen:
a) -7x2 +12x + 64 = 0
b) x2 - 6x + 9 = 0
Oplossing voor
Uit deze vergelijking kennen we de δ -determinant, omdat deze eerder als een voorbeeld werd berekend, dus we gaan er gebruik van maken en de oplosmiddelformule als volgt uitdrukken:
X1 = (-12+44)/ - 14 = - (32/14) = - (16/7)
X2 = (-12 -44) / -14 = 4
Oplossing B
Het vierkante trinomiale x2 - 6x + 9 is factoriseerbaar, omdat het een perfect vierkant trinomiaal is:
X2 - 6x + 9 = (x-3)2 = 0
De oplossing van deze vergelijking is x = 3.
- Oefening 3
Wat is de vergelijking waarvan de oplossingen 3 en 4 zijn?
Oplossing
De gefactoriseerde uitdrukking is:
(x - 3) ⋅ (x - 4) = 0
Distributieve onroerend goed toepassen:
X2 - 4x -3x + 12 = 0
De twee centrale termen zijn vergelijkbaar en kunnen worden verminderd, zijn: vertrekken:
X2 - 7x + 12 = 0
Referenties
- Baldor. 1977. Elementaire algebra. Venezolaanse culturele edities.
- Hoffman, J. Selectie van wiskundeproblemen. Deel 2.
- Jiménez, r. 2008. Algebra. Prentice Hall.
- Stewart, J. 2006. Precculment: wiskunde voor berekening. 5e. Editie. Cengage leren.
- Zapata, f. 4 manieren om een tweede graad vergelijking op te lossen. Hersteld van: Francesphysics.Blogspot.com.
- Zill, D. 1984. Algebra en trigonometrie. McGraw Hill.
- « Toevoeging polymeren structuur, kenmerken, functie, gebruik
- Intrinsieke motivatiekenmerken en voorbeelden »



\pm&space;\sqrt(-5)^2-4\times&space;3\times&space;22\times&space;3=)

^2-4c2)


x-\fracx(x+2)x+2=x(x+2))
=\frac-12\pm&space;44-14)