Arrhenius -vergelijking
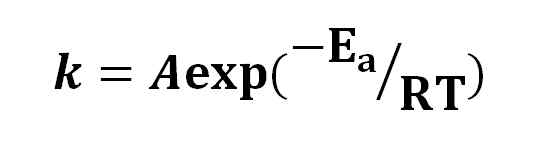
- 2163
- 79
- Aaron Okuneva
Wat is de Arrhenius -vergelijking?
De Arrhenius -vergelijking Het is een benadering die de snelheidsconstante van een chemische reactie relateert, afhankelijk van de temperatuur. Het werd opgericht in 1899 door de Zweedse chemicus Svante Arrhenius (1859-1927). Vertegenwoordigt een van de meest fundamentele bijdragen bij de ontwikkeling van chemische kinetiek.
Deze vergelijking is zijn theoretische bases te danken aan talloze wetenschappers, waaronder Wihelmy (1850), Berthelot (1862) en J. J. Hood (1885). Maar de grootste invloed wordt toegeschreven aan de oprichting van de Arrhenius -vergelijking aan het werk dat wordt gedaan door Van't Hoof (1884), die een afhankelijkheid van de evenwichtsconstanten van de chemische reacties met de temperatuur heeft vastgesteld met de temperatuur.
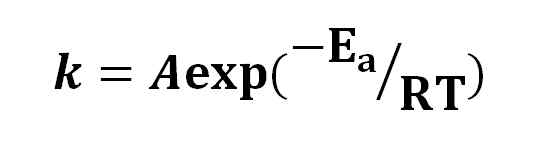 Arrhenius -vergelijking. Bron: Gabriel Bolívar.
Arrhenius -vergelijking. Bron: Gabriel Bolívar. Op basis van de Arrhenius -vergelijking is het idee dat een toename van 10 ºC een duplicatie van de reactiesnelheid heeft veroorzaakt, veroorzaakt. Andere interpretaties die het worden, is dat moleculen enige activeringsenergie nodig hebben om op elkaar te reageren.
Evenzo wordt erop gewezen dat de Arrhenius -vergelijking een andere vorm is van exponentiële desintegratie waarin de waarde van de snelheidsconstante afhankelijk van de exponent -Enaar/Rt, waar enaar is activeringsenergie.
Vergelijking en uitleg
De Arrhenius -vergelijking heeft de volgende twee uitdrukkingen:
K = AE-EA/RT
Vorm van de vergelijking die wordt gebruikt in de chemie en is gerelateerd aan reagensmol.
K = AE-EA/KBT
Vorm van de vergelijking die in de fysica wordt gebruikt en is gerelateerd aan de meer moleculen, dan met mollen.
Beide zijn afkomstig van de van 'Hoofvergelijking voor de variatie van de evenwichtsconstante K, afhankelijk van de temperatuur. De basisvergelijking is:
D (ln k)/dt = enaar/RT2
Het kan u van dienst zijn: dibenzalacetona: eigenschappen, reactiemechanisme, gebruik, risico'sDie is geïntegreerd, ervan uitgaandenaar is onafhankelijk van de temperatuur. Dus we hebben:
ln k = - enaar/Rt + ln a
Waar ln a de integratieconstante is. Wanneer de exponentiële functie aan beide zijden van de vergelijking wordt toegepast, verkrijgen we de reeds geïntroduceerde Arrhenius -vergelijking.
Componenten
k
Het is de snelheidsconstante van een chemische reactie. De waarde ervan kan worden verkregen, naast het gebruik van de Arrhenius -vergelijking, door de toepassing van de snelheidswet. Vertegenwoordigt het aantal botsingen tussen deeltjes geproduceerd door een reactie per seconde.
NAAR
Het is de zogenaamde pre-exponentiële factor, die de frequentie van botsingen tussen reagensmoleculen vertegenwoordigt met een geschikte geometrische oriëntatie die al dan niet een chemische reactie kan veroorzaken. Als de temperatuurvariatie van weinig grootte is, wordt deze meestal als constant beschouwd. Deze factor heeft zijn eigen formule:
A = z ρ
Waarbij z bekend staat als een frequentie- of botsingsfactor, en ρ de geometrische of sterische factor die de relatieve oriëntatie van de moleculen op het botspunt aangeeft. De constante A heeft dezelfde eenheden als de snelheidsconstante. In het geval dat er geen activeringsenergie is, zal de omvang van A gelijk zijn aan die van K.
ENnaar
Het is de activeringsenergie, die de drempel -energie vertegenwoordigt voordat de overgangsstat wordt bereikt.
Activatie -energie heeft de KJ/Mol -eenheid. Maar in de berekeningen wordt de J/Mol als eenheid gebruikt. Het minste (-) teken dat voorafgaat aan de Enaar, Het dient om aan te geven dat de toename ervan een afname van de reactiesnelheid veroorzaakt, evenals de afname ervan een toename van de reactiesnelheid oplevert.
Kan u van dienst zijn: gaschromatografieRT
Vertegenwoordigt de gemiddelde kinetische energie. Ondertussen is R de universele constante van gassen, een van de meest gebruikte waarden 8.31 J · K-1· Mol-1. En T is de absolute temperatuur die wordt uitgedrukt in Kelvin (K).
En
Het is de basis van natuurlijke of Neperiaanse logaritmen, met een waarde van 2.71828.
En-EA/RT
Het is de fractie van het reageren van moleculen met gelijke of overtollige energie in relatie tot activeringsenergie.
Toepassingen
De meeste toepassingen van de ARRHENIUS -vergelijking komen van gebruik bij het bepalen van de snelheidsconstante; en bij uitbreiding, de snelheid van de reactie, evenals de activeringsenergie.
Er is bijvoorbeeld een chemisch model ontwikkeld op basis van de Arrhenius -vergelijking, die de eigenschappen van de materialen kan voorspellen als hun temperatuurverandering, die worden toegepast op het gebied van geologie, constructie, engineering van materialen en in voedselwetenschap.
Het is toegepast, hoewel met bepaalde kritiek de Arhenius -vergelijking in de kinetiek van reacties van vaste toestand. Het is ook gebruikt om plantenreacties op waterstress te karakteriseren.
De Arenhius -vergelijking diende als basis voor het creëren van een wiskundig model, dat het effect van de temperatuur op de nuttige levensduur van de nikkelmetallische hydridecellen of batterijen kwantificeert.
Evenzo, op basis van de Arrhenius -vergelijking, werd de ontledingspercentage van varkensafval en kookolie vastgesteld, onder verschillende vochtinhoud.
Opgeloste oefeningen
Oefening 1
Wat is de activeringsenergie van een reactie als wordt vastgesteld dat zijn snelheidsconstante verdrievoudigt wanneer de temperatuur stijgt van 600 K tot 610 K?
Kan u van dienst zijn: fenoxyazijnzuur: synthese, procedure, gebruik, risico'sBeginnend bij de Arrhenius -vergelijking:
k = a · e-EA/RT
We wissen de factor A:
A = K1 / (e-EA/RT1))
Maar omdat we twee temperaturen hebben, T1 en t2, Er zullen twee snelheidsconstanten zijn: K1 en k2. Factor A verandert niet, dus we kunnen het matchen voor de tweede temperatuur:
k1 / (e-EA/RT1) = K2 / (e-EA/RT2))
En opruimen Enaar we zullen hebben:
ENnaar = R (ln k2/K1) / (1 / t1 - 1/t2))
Zoals2 is drie keer groter dan k1,
k2 / K1 = 3
ln (3) = 1.099
En aan de andere kant:
1 / t1 = 1/600 K = 1.66 x 10-3 K-1
1 / t2 = 1 /610 K = 1.64 x 10-3 K-1
Vervangen dan:
ENnaar = (8.31 J · K-1· Mol-1) (1.099) / (1.66 x 10-3 K-1 - 1.64 x 10-3 K-1))
= 456.5 kJ · mol-1
Oefening 2
In een gasfasereactie is activeringsenergie gelijk aan 103 kJ/mol, en de snelheidsconstante is 0.085 min-1. Bereken de snelheidsconstante bij 323 K.
Uit de vorige uitdrukking wissen we ln k2/K1:
ln k2/K1 = (Enaar/R) (1 /t1 - 1/t2))
Het juiste deel van de vergelijking ontwikkelen:
ln k2/K1 = (103.000 J · mol-1 / 8.31 J · K-1· Mol-1) (1/273 K - 1/323 K)
ln k2/K1 = 6.99
Antilogaritmen nemen:
k2/K1 = 1.086
k2 = (K1) (1.086)
= (0.085 min-1) (1.086)
= 0.092 min-1
Referenties
- Whitten, Davis, Peck & Stanley. (2008). Scheikunde. (8e ed.)). Cengage leren.
- Walter J. Moore. (1963). Fysische chemie. In chemische kinetiek. Vierde editie, Longmans.
- Iran. Levine. (2009). Principes van fysicochemie. Zesde editie. MC Graw Hill.
- Wikipedia. (2020). Arrhenius -vergelijking. Opgehaald uit: in.Wikipedia.borg
- Guenevieve del Mundo et al. (10 september 2020). Arrhenius -vergelijking. Hersteld van: chem.Librhetxts.borg
- Clark Jim. (2013). Rate constanten en de Arrhenius -vergelijking. Hersteld van: chemguide.co.Uk
- De redacteuren van Enyclopaedia Britannica. (2020). Arrhenius -vergelijking. Hersteld van: Britannica.com
- Helmestine, Anne Marie, pH.D. (28 augustus 2020). De Arrhenius -vergelijkingsformule en voorbeeld. Hersteld van: Thoughtco.com

