Domein en contradominium van een functie (met voorbeelden)

De concepten van domein en tegenspraak met een functie Ze worden vaak onderwezen in de berekeningscursussen die worden gegeven aan het begin van de universitaire carrière.

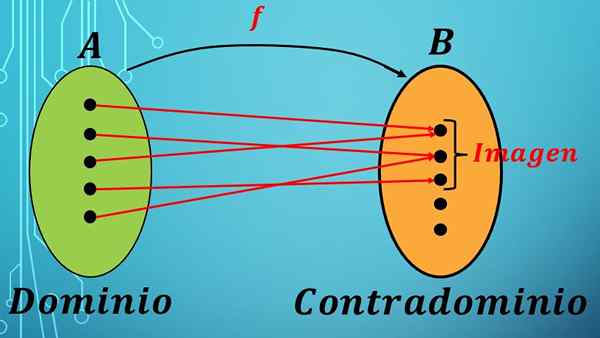
Voordat u domein en tegenstrijdigheid definieert, moet u weten wat een functie is. Een F -functie is een correspondentiewet (regel) tussen de elementen van twee sets.

Het geheel waarvan de elementen worden gekozen, wordt het domein van de functie genoemd, en de set waarnaar deze elementen worden verzonden door f wordt contradominium genoemd.

In de wiskunde wordt een functie met domein A en contradominium B aangeduid door expressie F: A → B.

De vorige uitdrukking zegt dat de elementen van set A worden verzonden naar Set B na de correspondentiewet f.

Een functie wijst elk element van de set toe aan een enkel element van set B.

Domein en tegenstrijdigheid

Gezien een echte functie van een echte variabele f (x), moet het domein van de functie al die reële getallen zijn, zodat, wanneer geëvalueerd in F, het resultaat een reëel getal is.

Over het algemeen is de tegenstelling van een functie de set reële nummers. De tegenstrijdigheid wordt ook de aankomst- of codominiumset van de F -functie genoemd.

De tegenstelling van een functie is altijd r?

Nee. Zolang de functie niet in detail wordt bestudeerd, wordt de reeks echte N -getallen meestal als tegenspraak beschouwd.

Maar zodra de functie is bestudeerd, kan een geschiktere set worden opgevat als contradominium, dat een subset van r zal zijn.

De juiste set die in de vorige paragraaf wordt genoemd, valt samen met de afbeelding van de functie.

De definitie van de afbeelding of het bereik van een functie F verwijst naar alle waarden die voortvloeien uit het evalueren van een element van het domein in F.

Domein- en tegenstrijdig voorbeelden

In de volgende voorbeelden, hoe het domein van een functie te berekenen en de afbeelding ervan wordt geïllustreerd.

voorbeeld 1

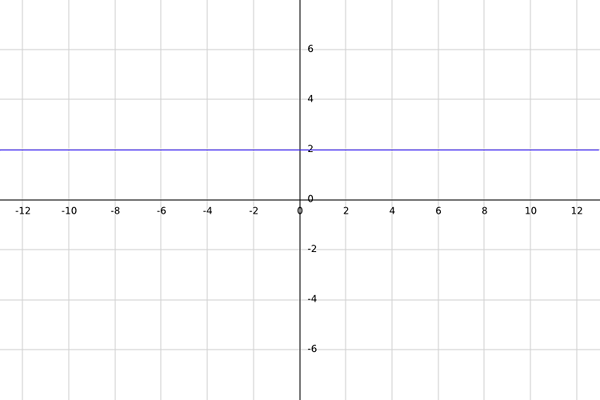
Laat F een echte functie zijn gedefinieerd door f (x) = 2.

De m -domein van F is allemaal reële getallen zodanig dat, bij het evalueren ervan in F, het resultaat een reëel getal is. De tegenstrijdigheid is voorlopig gelijk aan r.

Aangezien de gegeven functie constant is (altijd gelijk aan 2), moet het ongeacht welk reëel getal wordt gekozen, omdat bij het evalueren in F het resultaat altijd gelijk zal zijn aan 2, wat een reëel getal is.

Daarom is het domein van de gegeven functie allemaal reële getallen; dat wil zeggen a = r.

Nu het al bekend is dat het resultaat van de functie altijd gelijk is aan 2, is het beeld van de functie slechts nummer 2, daarom kan de tegenstelling van de functie opnieuw worden gedefinieerd als B = IMG (f) = 2.

Daarom f: r → 2.

Voorbeeld 2

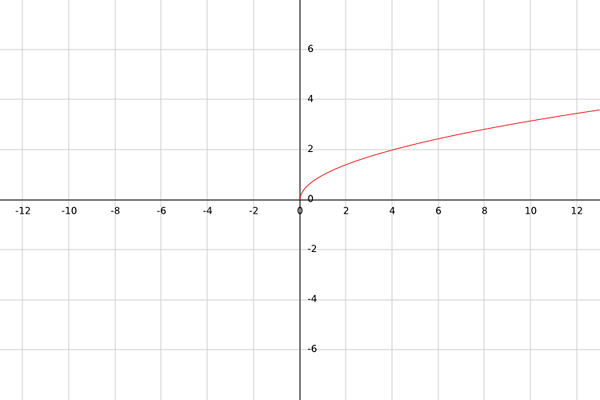
Laat G een echte functie zijn die wordt gedefinieerd door G (x) = √x.

Zolang het beeld van G niet bekend is, is het contradominium van G b = r.

Met deze functie moet rekening worden gehouden met dat vierkante wortels alleen worden gedefinieerd voor niet -negatieve getallen; dat wil zeggen, voor getallen groter dan of gelijk dan nul. √-1 is bijvoorbeeld geen echt getal.

Daarom moet de beheersing van de G -functie alle getallen groter dan of gelijk zijn dan nul; dat wil zeggen x ≥ 0.

Daarom a = [0,+∞).

Om het bereik te berekenen, moet worden opgemerkt dat elk resultaat van g (x), omdat het een vierkantswortel is, altijd groter zal zijn dan of gelijk aan. Dat wil zeggen, b = [0,+∞).

Concluderend, g: [0,+∞) → [0,+∞).

Voorbeeld 3

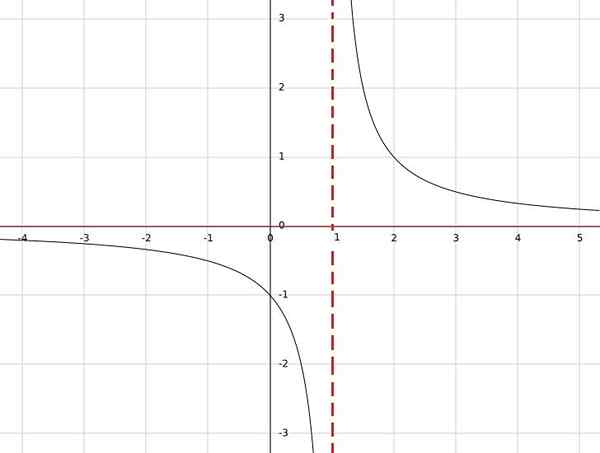
Als u de functie h (x) = 1/(x-1) hebt, wordt deze functie niet gedefinieerd voor x = 1, omdat deze in de noemer nul zou worden verkregen en de divisie door nul niet is gedefinieerd.

Aan de andere kant zal het resultaat voor elke andere echte waarde een reëel getal zijn. Daarom zijn domein allemaal Reais behalve één; dat wil zeggen a = r \ 1.

Op dezelfde manier is te zien dat de enige waarde die niet kan worden verkregen als resultaat is 0, omdat een fractie gelijk is aan nul, de teller nul moet zijn.

Daarom is de afbeelding van de functie de set van alle reais behalve nul, dan wordt het als contradominium b = r 0 beschouwd.

Tot slot, h: r \ 1 → r \ 0.

Waarnemingen

Domein en afbeelding hoeven niet dezelfde set te zijn, zoals aangetoond in voorbeelden 1 en 3.

Wanneer een functie in het Cartesiaanse vlak is, wordt het domein weergegeven door de X -as en het contradominium of het bereik wordt weergegeven door de Y -as.