120 divisors

De 120 divisors Het zijn al die cijfers die het precies verdelen. Deze cijfers zijn als volgt:

Divisors van 120 = 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 30, 40, 60, 120

Ook de tegenstellingen voor deze reeks getallen, dat wil zeggen de negatieven, zijn 120 divisors, omdat de divisie exact is. De 120 heeft 16 positieve hele delers en vele andere negatieven.

Er zijn verschillende manieren om de delers van een nummer te vinden. Als dit niet erg groot is, kunt u de vermenigvuldigingstabellen gebruiken (voor getallen minder dan 100) en verifiëren waarin tabellen het nummer in kwestie verschijnt. 12 verschijnt bijvoorbeeld in de tabellen van 2, 3, 4 en 6, en dit zijn hun divisors, samen met 1 en dezelfde 12.

Het aantal kan ook worden opgesplitst in zijn belangrijkste factoren, de deelname -regels toepassen en de factoren vermenigvuldigen. Maar u moet oppassen dat u geen divisie over het hoofd hebt doorstaan.

Omdat 120 groter is dan 100, is het niet direct in de vermenigvuldigingstabellen, maar het is niet te moeizaam om zijn 16 te vinden. Een geldige procedure voor alle nummers wordt onmiddellijk weergegeven, door het gebruik van zeer eenvoudige tabellen.

Hoeveel divisors is 120?

Ten eerste is het aantal delers van 120 ontdekt. Er is een formule waarmee je kunt weten hoeveel je hebt, hoewel het niet zegt wat ze zijn.

Samengestelde nummers, zoals 120, kunnen worden uitgedrukt als het product van priemgetallen of bevoegdheden hiervan. N -bellen naar een samengesteld nummer:

N = a^N ∙ B^M ∙ C^P … R^k

Kan u van dienst zijn: evenredigheidsrelaties: concept, voorbeelden en oefeningen

De getallen a, b, c ... r zijn priemgetallen en de waarden van n, m, p, ... k, de respectieve machten. De ontleding in topfactoren van 120 is als volgt:

120 | 2
60 | 2
30 | 2
15 | 3
5 | 5
1 | 1

Op deze manier is 120 het product van de factoren:

120 = 2³ ∙ 3 ∙ 5

Formule voor het berekenen van het aantal delers van n

Aantal divisors = (n +1) × (m +1) × (p +1)… × (k +1)

Nu wordt de formule op 120 toegepast. Van ontleding in factoren die u moet:

n = 3 (is de kracht van 2)

M = 1 (de 3 is verhoogd tot 1: 3¹ = 3)

P = 1 (de 5 lijkt ook verhoogd tot 1)

Met deze waarden:

Aantal divisors van 120 = (3 +1) × (1 +1) × (1 +1) = 4 × 2 × 2 = 16

Dit resultaat valt samen met het begin van het begin: 120 heeft 16 divisors. Bovendien is het al bekend dat de 2, 3 en 5 divisors van 120 zijn, evenals 10, omdat elk getal dat in 0 is afgewerkt, deelbaar is door 10. De procedure om ze allemaal te vinden, wordt onmiddellijk weergegeven.

Berekening van de delers van 120

Het wordt gedaan met behulp van de factoren die in de vorige sectie zijn berekend. Daar werd gezien dat de 2 een hoofdfactor is met exponent 3, en de 3 is een andere neeffactor, met exponent 1. Met deze informatie is de volgende tabel gebouwd:

Merk op dat de krachten van 2 beginnen in 2⁰ en eindigen in 2³, dat is de factor die ontstaat bij het ontbinden van 120. Onthoud dat 2⁰ en 3⁰ Beide zijn gelijk aan 1 (elk getal hoog tot 0 is 1). Voor factor 3 begint het in 3⁰ Tot 3¹, Sinds 3¹ = 3.

Vervolgens wordt de tabel voltooid met het product van de getallen in het rood, zoals hier getoond:

Kan u van dienst zijn: multiplicatief inverse: uitleg, voorbeelden, opgeloste oefeningen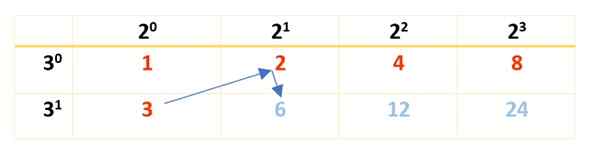

Alle rode en blauwe nummers zijn 120 divisors, maar er zijn amper 8. Om de resterende te vinden, is een nieuwe tabel barst, de divisors die al op de voorste rij zijn verkregen en de factor waarmee rekening moet worden gehouden, zijn geschreven: 5, met hun bevoegdheden in de eerste kolom, links, zoals deze:

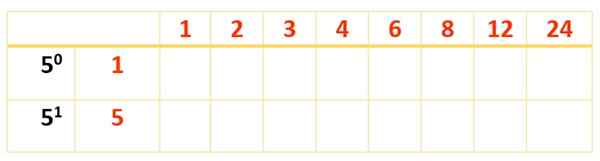
Nu wordt de tabel voltooid met de producten van de getallen in het rood, zoals met de eerste tabel werd gedaan:

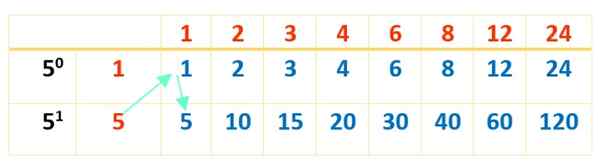
En ten slotte verschijnen de 16 divisors van 120 in Blue. De tabellen zijn een uitstekende hulp voor het op volgorde van bewerkingen en dus geen 120 deler.

Opgeloste oefeningen

De procedure om alle delers van een getal te vinden, is als volgt samengevat:

1. Het aantal opsplitsen in topfactoren.
2. Bereken het aantal divisors met de formule.
3. Bouw de benodigde tafels om delers te vinden. Als het aantal twee factoren heeft, is een tabel voldoende, als u drie factoren heeft, moeten twee tabellen worden gemaakt, zoals in het geval van 120.

Oefening 1

Vind alle delers van 288.

Oplossing

288 ontleedt in topfactoren:

288 | 2
144 | 2
72 | 2
36 | 2
18 | 2
9 | 3
3 | 3
1 | 1

De 288 is als volgt geschreven:

288 = 2⁵ ∙ 3²

Onmiddellijk is het aantal delers van 288 tot:

Aantal divisors = (n +1) × (m +1) × (p +1)… × (k +1)

Uit de ontleding in prime -factoren wordt opgemerkt dat n = 5 en m = 2, dan:

Divisors van 288 = (5 +1) × (2 +1) = 6 × 3 = 18

Er zijn 18 delers en omdat er slechts twee factoren zijn, is het voldoende met slechts één tabel:

Kan u van dienst zijn: kenmerken van de rechthoek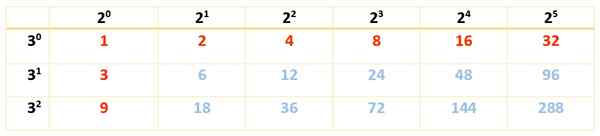

De divisors van 288 zijn de getallen in rood en in blauw:

Div (288) = 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 32, 36, 48, 72, 96, 144, 288

Ze kunnen snel worden gecontroleerd met behulp van een rekenmachine.

Oefening 2

Vind de delers van 350

Oplossing

350 ontbindingen:

350 | 2
175 | 5
35 | 5
7 | 7
1 | 1

De 350 kan worden geschreven als een product van drie factoren:

350 = 2 ∙ 5²∙ 7

De volgende stap is om te berekenen hoeveel divisors hebben, via de formule:

Aantal divisors = (n +1) × (m +1) × (p +1)… × (k +1)

Met n = 1, m = 2, p = 1

Divisors van 288 = (1 +1) × (2 +1) × (1 +1) = 2 × 3 × 2 = 12

Aangezien 350 drie factoren vereist, moeten er twee tafels worden gemaakt. De eerste is gedaan met 2 en 5², Maar het kan ook worden gedaan met 2 en 7, of met 7 en 5², Volgens de voorkeur is het eindresultaat in alle vormen hetzelfde:

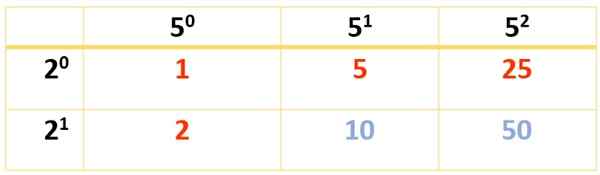
6 divisors worden verkregen. De anderen verschijnen met behulp van deze andere tabel:

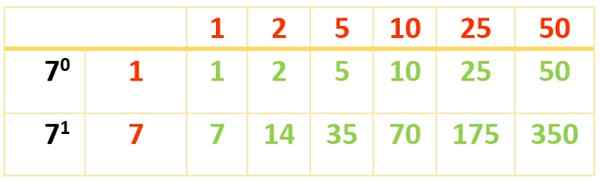
De divisors van 350 zijn:

Div (350) = 1, 2, 5, 7, 10, 14, 25, 35, 50, 70, 175, 350