Uniforme verdeling zet kenmerken, voorbeelden, toepassingen voort
- 4237
- 1191
- Pete Heaney V
Een willekeurige variabele heeft een Continue uniforme verdeling Als de kans om een waarde te nemen, binnen een eindig interval [a, b], hetzelfde is voor elke subinterval van gelijke lengte.
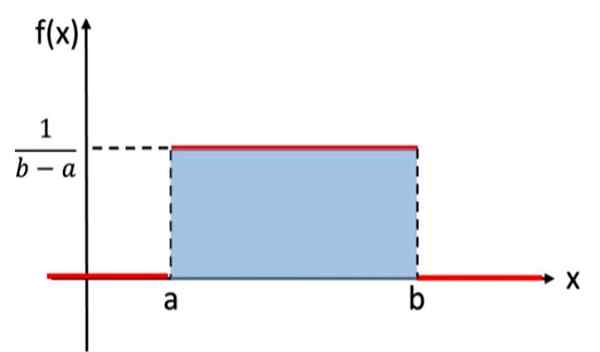
Deze verdeling is analoog aan de discrete uniforme verdeling, die aan elk resultaat van het willekeurige experiment dezelfde waarschijnlijkheid heeft toegewezen, maar in dit geval is de te overwegen variabele continu. Het experiment dat bestaat uit het selecteren van een willekeurig reëel getal, tussen waarden A en B, volgt de uniforme verdeling. Hier heb je je grafiek:
Figuur 1. Grafiek van de dichtheidsfunctie van de continue genormaliseerde uniforme verdeling In de wiskundige notatie heeft de continue uniforme verdeling een dichtheidsfunctie gedefinieerd als een functie in stukken of door secties, die kunnen worden geschreven als:
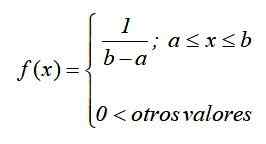
De grafiek van deze functie, bekend als Curve- of dichtheidsfunctie, Het is een rechthoek, dus de continue uniforme verdeling staat ook bekend als rechthoekige verdeling En het is de eenvoudigste van continue distributies.
Het gebied onder de grafiek van een waarschijnlijkheidsverdeling is gelijk aan 1 en neemt altijd positieve waarden aan. De uniforme verdeling voldoet aan deze criteria. Het is niet nodig om rechtstreeks te integreren om te controleren of het gebied 1 is, omdat het gebied van de gearceerde rechthoek in figuur 1 kan worden berekend met behulp van de formule:
Gebied = basis x hoogte = (b - a) x [1/(b - a)] = 1
Het kennen van het gebied onder de dichtheidscurve is erg belangrijk, omdat er een verband bestaat tussen het gebied en de kans op het optreden van een gebeurtenis, die voor deze verdeling in de volgende sectie wordt bepaald.
Continue uniforme verdelingskenmerken
De continue uniforme verdeling wordt gekenmerkt door zijn:
Dichtheidsfunctie
Laat X de continue willekeurige variabele zijn, die behoort tot het interval [a, b], dan:
Het kan u van dienst zijn: lineaire transformaties: eigenschappen, wat zijn het gebruik, typen, voorbeelden=\frac1b-a)
Distributie functie
Door middel van de distributiefunctie wordt de kans berekend dat de willekeurige variabele x een X -waarde uit de mogelijke waarden van het interval [a, b] neemt. Voor een continue verdeling wordt deze in het algemeen op deze manier berekend:
=\int_a^xf(x)dx)
In het geval van de continue uniforme verdeling is de kans f (x) gelijk aan het rechthoekige gebied waarvan de basis (x-a) is en de hoogte ervan (b-a) is:
=\int_a^x\left&space;(\frac1b-a&space;\right&space;)dx=\fracx-ab-a)
Wiskundig, als f (x) = pr (x = x) wordt de volgende functie vastgesteld door onderdelen, volgens het vorige resultaat:
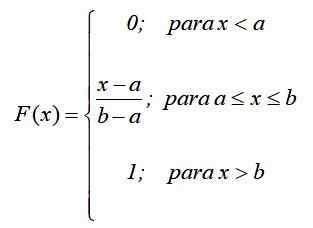
Op deze manier, wat eerder is gezegd: de waarschijnlijkheid hangt alleen af van de waarde van (X-A) en niet van de locatie in het interval [A, B]. De grafiek van de distributiefunctie is:
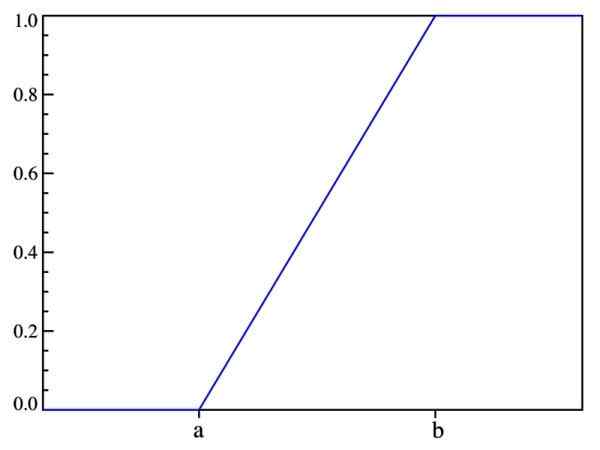Figuur 2. Grafiek van de distributiefunctie f (x). Bron: Wikimedia Commons. Verwachte waarde, variantie en standaardafwijking
Na het doen van talloze experimenten met de continue willekeurige variabele, wordt de gemiddelde waarde genoemd verwachte waarde, Het wordt aangeduid als E (x) en wordt berekend door de volgende integraal:
=\int_a^bxf(x)=\int_a^b\left&space;(\frac1b-a&space;\right&space;)xdx=\left&space;(\frac1b-a&space;\right&space;)\frac(b^2-a^2)2=\fraca+b2)
V (x) = e (x2) - EX)2
Daarom:
=\left&space;[\int_a^bx^2f(x)dx&space;\right&space;]-\left&space;(\fraca+b2&space;\right&space;)^2=\left&space;[\int_a^bx^2\left&space;(\fracb-a2&space;\right&space;)&space;dx\right&space;]-\left&space;(\fraca+b2&space;\right&space;)^2)
=\frac(b-a)^212)
D (x) = √ V (x)
=\sqrt\frac(b-a)^212)
Mediaan, mode, symmetrie en Curtosis
Het kan gemakkelijk worden geverifieerd dat de mediaan, die de centrale waarde van de uniforme verdeling is, gelijk is aan het gemiddelde, en omdat er geen waarde is die meer wordt herhaald dan andere, omdat ze allemaal even waarschijnlijk zijn in het interval [a, b ], mode bestaat niet.
Wat symmetrie betreft, is de uniforme verdeling symmetrisch en de Curtosis, die de mate is waarin de waarden rond het midden zijn geconcentreerd is -6/5.
Kan u van dienst zijn: wat zijn de 7 elementen van de omtrek?Voorbeelden
Verschillende situaties kunnen worden gemodelleerd door continue verdeling en dus hun gedrag voorspellen. Hier zijn enkele voorbeelden:
voorbeeld 1
Een bedrijf dat elektrische service biedt, biedt gelijkmatig gedistribueerde spanningsniveaus, tussen 123.0 V en 125.0 V. Dit betekent dat het in de binnenlandse opname mogelijk is om elke spanningswaarde te verkrijgen die tot dat interval behoort.
Vervolgens, zoals hierboven gezien, is de grafiek van de dichtheidsfunctie de rode rechthoek:
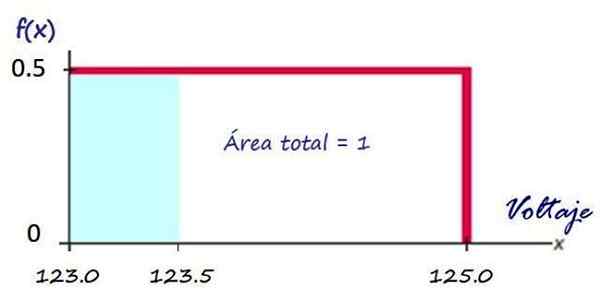figuur 3. Dichtheidsfunctie voor de spanning geleverd door een elektriciteitsbedrijf. Bron: f. Zapata. Het berekenen van de kans op het hebben van een spanning binnen het gegeven interval is bijvoorbeeld heel eenvoudig, bijvoorbeeld, wat de kans is dat het bedrijf een spanning zal sturen minder dan 123.5 V?
Deze waarschijnlijkheid is gelijk aan het gebied van de gearceerde rechthoek in blauw:
P (x<123.5) = (123.5 −123.0)x 0.5 = 0.25
En wat is de kans dat de geleverde spanning groter is dan 124.0 V?
Aangezien het totale gebied gelijk is aan 1, is de gezochte kans:
P (x> 124.0 V) = 1 - (1 × 0.5) = 0.5
Is logisch, sinds 124.0 is precies de waarde in het midden van het interval.
Voorbeeld 2
Een bepaalde willekeurige variabele X heeft een uniforme verdeling in het interval [0.100]. Bepalen:
a) De kans dat de waarde van X minder is dan 22.
b) De kans dat X waarden tussen 20 en 35 neemt.
c) De verwachte waarde, de variantie en de standaardafwijking van deze verdeling.
Antwoord op
Het wordt bepaald op het vorige voorbeeld, maar eerst moeten we de hoogte van de rechthoek bepalen, waardoor het totale gebied gelijk moet zijn aan 1:
Gebied = 100 × hoogte = 1
Daarom heeft de rechthoek een hoogte gelijk aan 1/100 = 0.01
Kan u van dienst zijn: Decagon: regelmatig, onregelmatig, eigenschappen, voorbeeldenP (x<22) = 22×0.01 = 0.22
Antwoord B
De gevraagde kans is gelijk aan het rechthoekige gebied waarvan de breedte is (35 - 20) en waarvan de hoogte 0 is.01:
P (22 Als u liever rechtstreeks naar de bovenstaande distributiefunctie gaat, moet u alleen de waarden vervangen in: P (20≤x≤35) = F (35) -f (20) Met f (x) gegeven door: F (x) = (x-a) / (b-a) De te introduceren waarden zijn: A = 0 B = 100 F (35) = (35-0) / (100-0) = 0.35 F (20) = (20-0) / (100-0) = 0.twintig P (20≤x≤35) = 0.35-0.20 = 0.vijftien De verwachte waarde is: E (x) = (a+b)/2 = (100+0)/2 = 50 De variantie is: V (x) = (b-a)2/12 = (100-0)2/12 = 833.33 En de standaardafwijking is: D (x) = √833.33 = 28.87 Deze verdeling is nuttig wanneer statistische simulatieprocessen worden uitgevoerd of bij het werken op gebeurtenissen waarvan de uiterlijk frequentie regelmatig is. Sommige programmeertalen genereren willekeurige getallen tussen 0 en 1, en zoals te zien uit de vorige voorbeelden, is de verdeling van de gevolg van de gevolg van waarschijnlijkheden uniform. In dit geval is het te overwegen interval [0,1]. Als u een experiment hebt waarin de gebeurtenissen regelmaat hebben, zoals hierboven uitgelegd, kunt u in principe elke dezelfde kans van optreden toewijzen. In dit geval biedt het probabilistische model van uniforme verdeling informatie voor de analyse. De uniforme verdeling wordt ook gebruikt bij de afronding van de verschillen tussen de waargenomen waarden en de reële waarden van een variabele, die volgens de afronding een uniforme verdeling van de fout in een bepaald interval uitgaan +0.5.Antwoord C
Toepassingen
Willekeurige nummers
Willekeurige distributiebemonstering
Foutafronding
Referenties