Oppervlakte -expansieformule, coëfficiënten en voorbeelden

De oppervlakkige verwijding Het is de uitbreiding die optreedt wanneer een object variaties van het oppervlak ervaart als gevolg van temperatuurvariatie. Het is te wijten aan de kenmerken van het materiaal of de geometrische vorm. Dilatatie overheerst in twee dimensies in dezelfde verhouding.

Bijvoorbeeld in een vel, wanneer er een variatie van temperatuur is, is dit het oppervlak van hetzelfde dat de grootste verandering lijdt als gevolg van thermische dilatatie.

Het oppervlak van een metalen plaat dat meestal op straat wordt gezien. Bron: Pixabay.

Het metalen vel van de vorige figuur verhoogt zijn breed en de lengte aanzienlijk wanneer het wordt verwarmd door zonnestraling. Integendeel, beide dalen aanzienlijk wanneer ze worden afgekoeld vanwege een daling van de omgevingstemperatuur.

Het is om deze reden dat, wanneer tegels op één verdieping worden geïnstalleerd, sommige randen met anderen niet moeten worden geraakt, maar er moet een scheidingsruimte zijn genaamd Dilatation Board.

Bovendien is deze ruimte gevuld met een speciaal mengsel dat een zekere mate van flexibiliteit heeft, waardoor tegels worden voorkomen dat kraken door sterke drukken die thermische dilatatie kan produceren.

[TOC]

Wat is oppervlakkige verwijding?

In een vast materiaal behouden atomen hun meer of minder vaste relatieve posities rond een balanspunt. Vanwege thermische agitatie oscilleren ze er echter altijd omheen.

Door de temperatuur te verhogen, neemt ook de thermische oscillatie toe, waardoor gemiddelde oscillatieposities veranderen. Dit komt omdat het linkpotentieel niet bepaald parabolisch is en asymmetrie heeft rond het minimum.

Hieronder staat een figuur dat de energie van de chemische binding schetst, afhankelijk van de interatomaire afstand. De totale oscillatie -energie bij twee temperaturen wordt ook getoond en hoe het oscillatiecentrum beweegt.

Het kan je van dienst zijn: Pascal Tonel: How It Works and Experimenten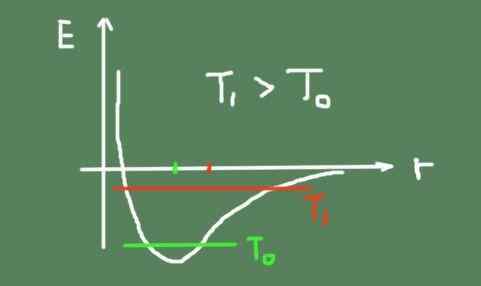Link Energy Graph versus Interatomic Distance. Bron: zelf gemaakt.

Oppervlakkige verwijding en de coëfficiënt ervan

Om de oppervlakkige dilatatie te meten, beginnen we uit een initiële gebied A en een begintemperatuur T, van het object waarvan de dilatatie moet worden gemeten.

Stel dat dit object een lamina van gebied A is, en de dikte ervan is veel lager dan de vierkantswortel van het gebied a. Het vel wordt onderworpen aan een AT -temperatuurvariatie, zodat de eindtemperatuur van hetzelfde zodra de thermische balans met de warmtebron zal worden vastgesteld, T '= T+ Δt zal zijn.

Tijdens dit thermische proces zal het oppervlak ook zijn gewijzigd in een nieuwe waarde bij '= a + ΔA. Aldus wordt de oppervlaktedilatiecoëfficiënt σ gedefinieerd als de verhouding tussen de relatieve variatie van oppervlakte per eenheid van temperatuurvariatie.

De volgende formule definieert de oppervlakkige dilatatiecoëfficiënt σ:

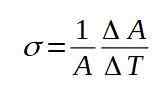
De oppervlakkige dilatatiecoëfficiënt σ is praktisch constant voor een breed bereik van temperatuurwaarden.

Vanwege de definitie van σ zijn de afmetingen ervan inverse temperatuur. Als eenheid wordt het meestal gebruikt ° C^-1.

Oppervlaktedilatatiecoëfficiënt voor verschillende materialen

Vervolgens zullen we een lijst geven van de oppervlakkige dilatatiecoëfficiënt voor sommige materialen en elementen. De coëfficiënt wordt berekend in normale atmosferische druk op basis van een omgevingstemperatuur van 25 ° C en de waarde ervan wordt als constant beschouwd in een bereik van AT van -10 ° C tot 100 ° C.

De eenheid van de oppervlakkige dilatatiecoëfficiënt zal zijn (° C)^-1

- Staal: σ = 24 ∙ 10^-6 (° C)^-1

- Aluminium: σ = 46 ∙ 10^-6 (° C)^-1

Het kan u van dienst zijn: magnetisatie: orbitaal en spin magnetisch moment, voorbeelden

- Goud: σ = 28 ∙ 10^-6 (° C)^-1

- Koper: σ = 34 ∙ 10^-6 (° C)^-1

- Messing: σ = 36 ∙ 10^-6 (° C)^-1

- IJzer: σ = 24 ∙ 10^-6 (° C)^-1

- Glas: σ = (14 tot 18) ∙ 10^-6 (° C)^-1

- Kwarts: σ = 0,8 ∙ 10^-6 (° C)^-1

- Diamant: σ = 2 ,, 4 ∙ 10^-6 (° C)^-1

- Lead: σ = 60 ∙ 10^-6 (° C)^-1

- Eiken hout: σ = 108 ∙ 10^-6 (° C)^-1

- PVC: σ = 104 ∙ 10^-6 (° C)^-1

- Koolstofvezel: σ = -1,6 ∙ 10^-6 (° C)^-1

- Beton: σ = (16 tot 24) ∙ 10^-6 (° C)^-1

De meeste materialen strekken zich uit met een temperatuurstijging. Sommige materialen zoals koolstofvezel voldoen echter aan de temperatuurstijging.

Opgeloste voorbeelden van oppervlakkige verwijding

voorbeeld 1

Een stalen plaat heeft afmetingen van 3m x 5 m. 'S Ochtends en in de schaduw is de temperatuur 14 ° C, maar' s middags verwarmt de zon het tot 52 ° C. Vind het laatste deel van de plaat.

Oplossing

We beginnen met de definitie van oppervlakkige dilatatiecoëfficiënt:

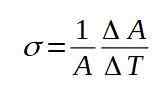
Vanaf hier wissen we de variatie in het gebied:

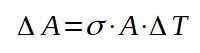
Vervolgens gaan we verder met het vervangen van de respectieve waarden om de toename van het gebied te vinden met de temperatuurstijging.

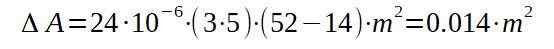
Dat wil zeggen, het uiteindelijke gebied zal 15.014 vierkante meter zijn.

Voorbeeld 2

Laat zien dat de oppervlakkige dilatatiecoëfficiënt ongeveer twee keer de lineaire dilatatiecoëfficiënt is.

Oplossing

Stel dat we beginnen met een rechthoekige plaat met breedte afmetingen LX en lange ly, dan zal het oorspronkelijke gebied a = lx ∙ ly zijn

Kan u van dienst zijn: thermometrische schalen

Wanneer de plaat een temperatuurstijging van AT lijdt, dan nemen de afmetingen ook toe zijn nieuwe breedte Lx 'en zijn nieuwe' lang, zodat zijn nieuwe gebied een '= lx' ∙ ly 'zal zijn

De variatie die door het plaatoppervlak wordt geleden als gevolg van temperatuurverandering zal dan zijn

Δa = lx '∙ ly' - lx ∙ ly

waarbij lx '= lx (1 + α Δt) en ly' = ly (1 + α Δt)

Dat wil zeggen dat de verandering van het gebied afhankelijk van de lineaire dilatatiecoëfficiënt en de temperatuurverandering zal zijn:

ΔA = lx (1 + α Δt) ∙ ly (1 + α Δt) - lx ∙ ly

Dit kan worden herschreven als:

Δa = lx ∙ ly ∙ (1 + α Δt) ² - lx ∙ ly

Het ontwikkelen van het vierkant en het vermenigvuldigen hebben we het volgende:

I

Zoals α in de orde van 10 is^-6, Door het vierkant op te voeden, is het de volgorde van 10^-12. Aldus is de kwadratische term in de vorige uitdrukking verachtelijk.

Dan kan de toename van het gebied worden benaderd door:

Δa ≈ 2a Δt lx ∙ ly

Maar de toename van het gebied, afhankelijk van de oppervlakkige dilatatiecoëfficiënt is:

ΔA = γ Δt a

Van waar een uitdrukking wordt afgeleid die de lineaire dilatatiecoëfficiënt relateert aan de oppervlakkige dilatatiecoëfficiënt.

γ ≈ 2 ∙ α

Referenties

1. Bauer, W. 2011. Fysica voor engineering en wetenschappen. Deel 1. Mac Graw Hill. 422-527
2. Giancoli, D. 2006. Fysica: principes met toepassingen. 6e. Editie. Prentice Hall. 238-249.