Verschil tussen cirkel en omtrek (met voorbeelden)

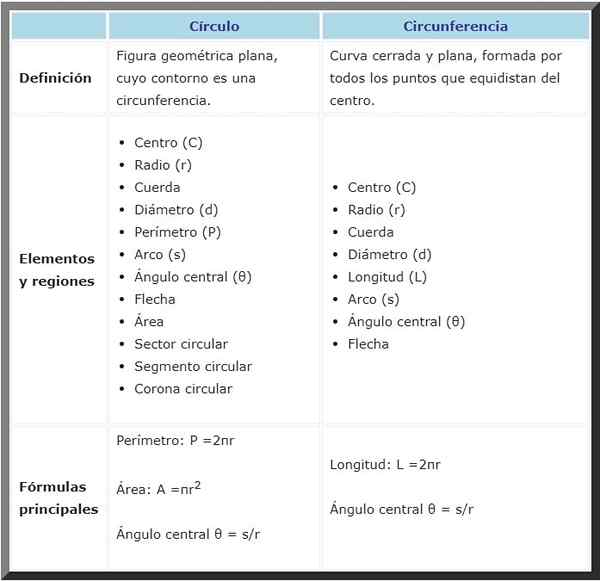
De Verschil tussen cirkel en omtrek Het is de volgende: de cirkel is een plat, voorgevormd of afgebakend oppervlak door een cirkel, terwijl de laatste een platte curve is.

Vaak zijn beide concepten in de war, omdat ze gerelateerd zijn, maar je moet altijd onthouden dat de omtrek de rand van de cirkel is, terwijl het de omtrek en alle punten bevat.

Beide hebben veel gemeenschappelijke elementen, zoals het centrum, de straal en de diameter, onder andere, volgens de volgende vergelijkende tabel:

	Cirkel	Omtrek
Definitie	Vlakke geometrische figuur, waarvan de contour een omtrek is.	Gesloten en platte curve, gevormd door alle punten die in het midden gelijk zijn.
Elementen en regio's	Centrum (c) Radio (R) Touw Diameter (D) Perimeter (P) Boog (s) Centrale hoek (Θ)) Pijl Gebied Circulaire sector Cirkelvormig segment Cirkelvormige kroon	Centrum (c) Radio (R) Touw Diameter (D) Lengte (l) Boog (s) Centrale lengte (Θ)) Pijl
Formules	Perimeter: P = 2π⋅R Gebied: a =πR2 Centrale hoek: Θ= S/R	Lengte: l = 2π⋅R Centrale hoek: Θ= S/R

[TOC]

Cirkel: definitie, kenmerken en onderdelen

Een cirkel is een platte geometrische figuur, die alle punten van de omtrek omvat die de contour vormt en ook alle interieurpunten.

Om deze reden wordt het gekenmerkt door te hebben:

-Rand of perimeter, wat de cirkelomtrek is.

-Een oppervlakkig gebied.

De elementen van de cirkel

Elke cirkel heeft de volgende onderdelen of elementen:

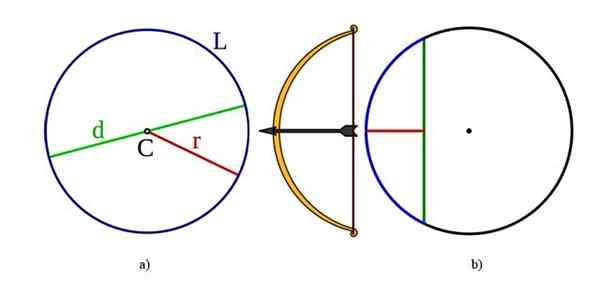Elementen van de cirkel, ook gemeenschappelijk voor de omtrek: links in a) zijn de middelste d, diameter d, straal r en lengte l l. Rechts op B) Er zijn het touw en de sagita of de pijl. Bron: Wikimedia Commons.

Centrum: Wat is punt C, dat alle punten van de rand equidisteert.

Kan u dienen: boog (geometrie): maat, soorten bogen, voorbeelden

Touw: segment dat twee punten van de rand van de cirkel verbindt. In figuur B) aan de rechterkant is het het donkerdere groene segment.

Diameter: lichter groen segment, aangeduid als "D" in figuur A), die twee punten van de rand verbindt en tegelijkertijd door het midden gaat. De diameter is ook een touw, de langste van allemaal, dus het staat bekend als de Groot touw.

Radio: aangeduid door "r" in figuur A), het is het rode segment dat zich bij het midden van de cirkel verbindt met een punt van de rand. De maat is de helft van de diameter.

Boog: een deel van de contour dat tussen twee punten hiervan is, in blauw in figuur B).

Centrale hoek: Het is de hoek waarvan het hoekpunt zich in het midden bevindt of en de zijkanten zijn radio's van de cirkel.

Pijl: segment loodrecht op een touw (in rood in figuur B), dat het midden van het touw met een punt van de rand verbindt.

Lengte of omtrek: Het is de maat van de cirkelcontour, aangeduid als l. Het hangt af van Radio R en is evenredig met het irrationele getal π:

π = 3.1416 ..

Zodat:

L = 2π⋅r

Cirkelvormige gebieden

Als een plat figuur heeft de cirkel een totale oppervlakte en ook verschillende regio's. De bekendste zijn de volgende:

Cirkelgebied: Het is evenredig met het kwadraat van de straal, de evenredigheidsconstante is het getal π.

Het Circle -gebied bellen, wordt uitgedrukt als:

A = πr²

Cirkelvormig segment: Het is een deel van de cirkel beperkt door de blauwe boog en het donkergroene touw in figuur B.

Kan u van dienst zijn: aanvullende hoeken: wat zijn, berekening, voorbeelden, oefeningen

Circulaire sector: Het is ook een regio van de cirkel, maar bevatte tussen twee radio's en de bijbehorende boog.

Cirkelvormige kroon: Het heeft de vorm van een ring en wordt beperkt door twee concentrische omtrek, buiten die van Radio Menor en binnen de radio -burgemeester.

Omtrek: DEfinitie, kenmerken en onderdelen 

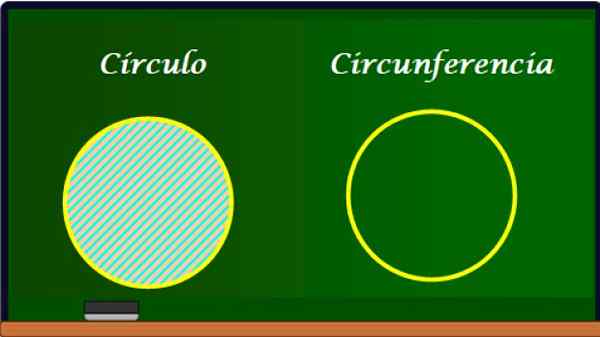Een cirkel en zijn omtrek. Bron: f. Zapata.

De omtrek is de rand van de cirkel en heeft daarom veel elementen gemeen. De omtrek heeft echter geen gebied, want omdat het een curve is, heeft het alleen lengte l.

De omtrek wordt formeel gedefinieerd als de set van alle punten die overeenkomen met een ander punt dat bekend staat als het centrum.

De interieurpunten zijn niet inbegrepen, omdat deze overeenkomen met de cirkel.

De elementen van de omtrek

Veel van de elementen van de omtrek zijn dezelfde als die van de cirkel, exclusief die welke verwijzen naar gebieden en regio's, dus de bovenste figuur dient als referentie.

We hebben dan:

Centrum: aangeduid door C en soms ook als O, houden alle punten van de omtrek dezelfde afstand bij.

Touw: segment dat samenkomt met twee punten van de omtrek.

Diameter: Het voegt ook twee punten van de omtrek, maar gaat altijd door het centrum van hetzelfde.

Radio: Het is de afstand tussen het midden en elk punt van de omtrek.

Boog: Het is een deel van de omtrek.

Centrale hoek: Het is de hoek met het hoekpunt in het midden C en twee gelijke kanten die net als de radio meten.

Pijl: segment loodrecht op een touw, dat zich bij het midden hiervan verbindt met het overeenkomstige punt van de omtrek.

Kan u van dienst zijn: multiplicatief principe: teltechnieken en voorbeelden

Lengte of omtrek: Het is de maat van de omtrek, die zoals we hebben gezien, evenredig is met het nummer π = 3.1416 ... en het wordt berekend door de formule:

L = 2π⋅r

De omtrekvergelijking

Een punt P behoort tot een omtrek zolang zijn afstand tot een ander punt C gelijk is aan R, de radio.

Elk punt op het Cartesiaanse vlak heeft coördinaten (X, y) en het kwadraat van afstand D Tussen twee van hen, p₁(X₁,En₁) En P₂(X₂,En₂), wordt gegeven door de formule:

D₂² = (x₂ - X₁))² +  (En₂ - En₁))²

Laten we op het punt van coördinaten (x, y) gaan en punt C (h, k) coördineren. Vervangen, de vorige vergelijking zou zo zijn:

(X - h)² +  (Y- k)² = r²

Dit is de omtrekvergelijking, dat elk punt daarop voldoet. Als het midden van de omtrek samenvalt met de oorsprong van het coördinatensysteem, dan is h = k = 0 en de vergelijking is vereenvoudigd:

X² + En² = r²

Laten we eens kijken naar een voorbeeld van het gebruik van de vergelijking en dit probleem kunnen beantwoorden: behoort het punt (4.6) tot de omtrek (x - 1)² +  (en - 2)² = 25?

Om erachter te komen dat de coördinaten van het punt in de vergelijking worden vervangen, en als het een gelijkheid is, behoort het punt tot de omtrek:

(4 - 1)² +  (6 - 2)² = 3² + 4² = 9 + 16 = 25

En inderdaad, als 25 = 25, wordt geconcludeerd dat (4.6) wel tot de omtrek behoort.

Referenties

1. Gratis wiskunde tutorials. Gebied en perimeter van een cirkel - geometriecalculator. Hersteld van: Analyzemath.com.
2. Math Open Referentie. Omtrek, perimeter van een cirkel. Hersteld van: Mathpenref.com.
3. Wetenschap. Hoe u de omtrek van een cirkel kunt vinden. Hersteld van: wetenschap.com.
4. Stewart, J. 2006. Precculment: wiskunde voor berekening. 5e. Editie. Cengage leren.
5. Zill, D. 1984. Algebra en trigonometrie. McGraw Hill.