Additieve ontleding

De Additieve ontleding van een positief geheel getal is om het uit te drukken als een som van twee of meer positieve getallen. We hebben dus dat nummer 5 het kan uitdrukken als 5 = 1+4, 5 = 2+3 of 5 = 1+2+2. Elk van deze manieren om nummer 5 te schrijven is wat we additieve ontleding zullen noemen.

Als we opletten, kunnen we zien dat uitdrukkingen 5 = 2+3 en 5 = 3+2 dezelfde compositie vertegenwoordigen; Beide hebben dezelfde cijfers. Alleen voor een kwestie van comfort wordt echter meestal elk van de advertenties geschreven die de criteria volgen van het minst naar het grootste.

Additieve ontleding

Als een ander voorbeeld kunnen we nummer 27 nemen, dat we het kunnen uitdrukken als:

27 = 7+10+10

27 = 9+9+9

27 = 3+6+9+9

27 = 9+18

Additieve ontleding is een zeer nuttig hulpmiddel waarmee we onze kennis over nummeringssystemen kunnen versterken.

Canonieke additieve ontleding

Wanneer we aantallen meer dan twee cijfers hebben, is een bepaalde vorm van het ontbinden ervan in de veelvouden van 10, 100, 1000, 10.000, enz., die het goedmaken. Deze manier om elk getal te schrijven wordt canonieke additieve ontleding genoemd. Nummer 1456 kan het bijvoorbeeld als volgt ontbinden:

1456 = 1000 + 400+ 50 + 6

Als we het nummer 20 846 295 hebben, zal uw canonieke additieve ontleding zijn:

20 846 295 = 20 000 000 + 800 000 + 40 000 + 6000 + 200 + 90 +5.

Dankzij deze ontleding kunnen we zien dat de waarde van een bepaald cijfer wordt gegeven door de positie die het inneemt. Laten we als voorbeeld de nummers 24 en 42 nemen:

24 = 20 + 4

42 = 40 +2

Hier kunnen we zien dat in 24 de 2 een waarde heeft van 20 eenheden en op 4 een waarde van 4 eenheden; Aan de andere kant heeft de 4 in 42 een waarde van 40 eenheden en de 2 van twee eenheden. Hoewel beide getallen dezelfde cijfers gebruiken, zijn hun waarden dus totaal verschillend door de positie die ze innemen.

Kan je van dienst zijn: x kwadraat

Toepassingen

Een van de toepassingen die we kunnen geven aan additieve ontleding is in bepaalde soorten demonstraties, waarin het zeer nuttig is om een ​​positief geheel getal te zien als de som van anderen.

Voorbeeld stelling

Laten we als voorbeeld de volgende stelling nemen met hun respectieve demonstraties.

- Wees z een heel getal van 4 cijfers, dan is z deelbaar met 5 als de figuur die overeenkomt met de eenheden nul of vijf is.

Demonstratie

Laten we onthouden wat deelname is. Als we "A" en "B" hele getallen hebben, zeggen we dat "een" Divides "B" als er een gehele getal "C" is, zodat B = A*C.

Een van de eigenschappen van de scheidbaarheid vertelt ons dat als "A" en "B" deelbaar zijn tussen "C", de aftrekking "A-B" ook is.

Wees z een heel aantal van 4 cijfers; Daarom kunnen we schrijven naar Z en Z = ABCD.

Met behulp van canonieke additieve ontleding moeten we:

Z = a*1000 + b*100 + c*10 + d

Het is duidelijk dat A*1000 + B*100 + C*10 deelbaar is tussen 5. Daarom hebben we dat z deelbaar is tussen 5 als z - (a*1000 + b*100 + c*10) deelbaar is tussen 5.

Maar z - (a*1000 + b*100 + c*10) = d en d is een enkel figuurnummer, dus de enige manier om deelbaar te zijn tussen 5 is dat het 0 of 5 is.

Daarom is z deelbaar tussen 5 als d = 0 of d = 5.

Merk op dat als Z n -cijfers heeft, de demonstratie exact hetzelfde is, het alleen verandert dat we nu Z = a zouden schrijven₁NAAR₂… NAAR_N En het doel zou zijn om dat te bewijzen_N is nul of vijf.

Partities

We zeggen dat een verdeling van een positief geheel getal een manier is waarop we een nummer kunnen schrijven als een som van positieve gehele getallen.

Kan u van dienst zijn: Convergence Radio: Definitie, voorbeelden en oefeningen opgelost

Het verschil tussen een additieve ontleding en een partitie is dat, hoewel in de eerste wordt gevraagd dat het tenminste kan worden opgesplitst in twee of meer, in de partitie deze beperking.

We hebben dus het volgende:

5 = 5

5 = 1+4

5 = 2+3

5 = 1+2+2

Bovenstaande zijn partities van 5.

Dat wil zeggen, we hebben dat alle additieve ontleding een partitie is, maar niet alle partitie is noodzakelijkerwijs een additieve ontleding.

In getallen theorie garandeert de fundamentele stelling van rekenkunde dat elk hele aantal uniek kan worden geschreven als een product van neven en nichten.

Wanneer de partities worden bestudeerd, is het doel om te bepalen op hoeveel manieren een positief geheel getal kan worden geschreven als de som van andere gehele getallen. Daarom definiëren we de partitiefunctie zoals hieronder gepresenteerd.

Definitie

Partitie P (n) functie wordt gedefinieerd als het aantal manieren waarop een positief geheel getal N kan worden geschreven als een som van positieve gehele getallen.

Terugkerend naar het voorbeeld van 5, moeten we:

5 = 5

5 = 1+4

5 = 2+3

5 = 1+1+3

5 = 1+2+2

5 = 1+1+1+2

5 = 1+1+1+1+1

Op deze manier, P (5) = 7.

Grafieken

Zowel partities als additieve ontledingen van een getal n kunnen geometrisch worden weergegeven.  Stel dat we een additieve ontleding van n hebben. In deze ontleding kunnen de addends worden opgelost zodat de leden van de som worden besteld van het minst tot de grootste. Dus het is de moeite waard:

n = a₁ + naar₂ + naar₃ +… + A_R met

naar₁ ≤ a₂ ≤ a₃ ≤ ... ≤ a_R.

We kunnen de ontleding als volgt grafieken: op een eerste rij markeren we de a₁-punten, dan markeren we in het volgende₂-punten, enzovoort tot het reiken_R.

Kan u van dienst zijn: ongelijkheid van de driehoek: demonstratie, voorbeelden, opgeloste oefeningen

Laten we als voorbeeld nummer 23 nemen en de volgende ontleding ervan:

23 = 5 + 4 + 7 + 3 + 1 +3

We bestellen deze ontleding en we hebben:

23 = 1 + 3 + 3 + 4+ 5 + 7

De bijbehorende grafiek zou zijn:

Evenzo, als we deze grafiek in plaats daarvan horizontaal verticaal lezen, kunnen we een ontleding verkrijgen die mogelijk anders is dan de vorige. In het voorbeeld van de 23 valt het volgende op:

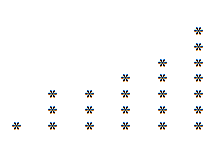
Dus we hebben die 23, we kunnen het ook schrijven als:

23 = 6 + 5 + 5 + 3 + 2 + 1 + 1.