Gedeeltelijke derivatenigenschappen, berekening, oefeningen

De Gedeeltelijke derivaten van een functie met verschillende onafhankelijke variabelen zijn die welke worden bereikt door het gewone derivaat in een van de variabelen te nemen, terwijl de anderen worden onderhouden of als constanten worden beschouwd.

Het gedeeltelijke derivaat in een van de variabelen, bepaalt hoe de functie op elk punt varieert, per eenheid van verandering de variabele in kwestie. 

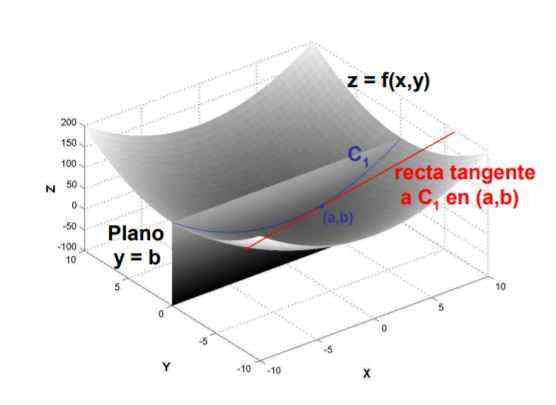Figuur 1. De helling van de raaklijn naar de curve gevormd door de kruising van het vlak y = b met het oppervlak f (x, y) op punt (a, b) is de gedeeltelijke afgeleide van f ten opzichte van x, geëvalueerd op dat punt. Bron: UPM.is

Vanwege de definitie ervan wordt het gedeeltelijke derivaat berekend met de wiskundige limiet van het quotiënt tussen de variatie van de functie en de variatie van de variabele ten opzichte van wat is afgeleid, wanneer de verandering van deze laatste neigt naar nul.

Stel dat het geval van een functie F Het hangt af van de variabelen X En En, dat wil zeggen voor elk paar (X, y) A wordt toegewezen Z: 

f: (x, y) → z .

De gedeeltelijke afgeleide van de functie z = f (x, y), met betrekking tot X is gedefinieerd als:

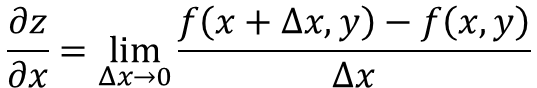
Nu zijn er verschillende manieren om de gedeeltelijke afgeleide van een functie aan te duiden, bijvoorbeeld:

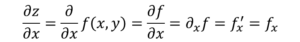
Het verschil met de gewone derivaat, in termen van notatie, is dat de D van afleiding wordt gewijzigd in het symbool ∂, Bekend als "Jacobi D".

[TOC]

Eigenschappen van gedeeltelijke derivaten

De gedeeltelijke afgeleide van een functie van verschillende variabelen, met betrekking tot een van hen, is de gewone derivaat in genoemde variabele en de rest als vast of constant beschouwen. Om het gedeeltelijke derivaat te vinden, kunnen de afleidingregels van gewone derivaten worden gebruikt.

Onder de belangrijkste eigenschappen:

Kan u van dienst zijn: gemeenschappelijke factor voor het groeperen van termen: voorbeelden, oefeningen

Continuïteit

Als een functie F (x, y) heeft gedeeltelijke derivaten in X En En op het punt (Xo, ik) dan kan worden gezegd dat de functie op dat moment continu is.

Kettingregel

Een functie F (x, y) Met continue gedeeltelijke derivaten in X En En, die op zijn beurt afhangt van een parameter T door x = x (t) En y = y (t), Het heeft een gewone afgeleide ten opzichte van de variabele T, die wordt berekend door de kettingregel:

D_T Z = ∂_XZ D_Tx + ∂_EnZ D_TEn

Eigenschap sluiten of vergrendelen

Het gedeeltelijke afgeleide met betrekking tot een van de variabelen van een functie F van twee of meer variabelen (X, y, ...), Het is een andere functie G In diezelfde variabelen bijvoorbeeld: 

G (x, y, ...) = ∂_En F (x, y, ...)

Dat wil zeggen, gedeeltelijke afleiding is een operatie die van r gaat^N a r^N. In die zin wordt gezegd dat het een gesloten werking.

Opeenvolgende gedeeltelijke derivaten

De opeenvolgende gedeeltelijke derivaten van een functie van verschillende variabelen kunnen worden gedefinieerd, waardoor nieuwe functies in dezelfde onafhankelijke variabelen aanleiding geven.

Wees de functie F (x, y). De volgende opeenvolgende derivaten kunnen worden gedefinieerd:

F_Xx = ∂_XF ;  F_Yy = ∂_YyF ; F_XY = ∂_XYF En F_Yx = ∂_YxF

De laatste twee staan ​​bekend als Gemengde derivaten Omdat ze twee verschillende onafhankelijke variabelen met zich meebrengen.

Schwarz Stelling

Wees een functie F (x, y), op een zodanige manier gedefinieerd dat zijn gedeeltelijke derivaten continue functies zijn in een open subset van R².

Dus voor elke paren (X, y) Dat ze tot de genoemde subset behoren, zijn de gemengde derivaten identiek:

∂_XYF = ∂_YxF

De vorige verklaring staat bekend als Schwarz Stelling.

Hoe worden gedeeltelijke derivaten berekend?

Gedeeltelijke derivaten worden berekend vergelijkbaar met gewone functiesderivaten in een enkele onafhankelijke variabele. Wanneer de gedeeltelijke afgeleide van een functie van verschillende variabelen wordt genomen met betrekking tot een van hen, worden de andere variabelen als constanten beschouwd.

Kan u van dienst zijn: de helft van 15

Hieronder staan ​​verschillende voorbeelden:

voorbeeld 1

Wees de functie:

f (x, y) = -3x² + 2 (en - 3)²

Er wordt gevraagd om de eerste gedeeltelijke afgeleide te berekenen met betrekking tot X en de eerste gedeeltelijke afgeleide met betrekking tot En.

Procedure

Om het gedeeltelijke te berekenen F met betrekking tot X, Is bezet En als constant:

∂_XF = ∂_X(-3X² + 2 (en - 3)² ) = ∂_X(-3X² )+ ∂_X(2 (en - 3)² ) = -3 ∂_X(X²) + 0 = -6x.

En op zijn beurt, om het afgeleide te berekenen met betrekking tot En Is bezet X als constant:

∂_EnF = ∂_En(-3X² + 2 (en - 3)² ) = ∂_En(-3X² )+ ∂_En(2 (en - 3)² ) = 0 + 2 · 2 (y - 3) = 4y - 12.

Voorbeeld 2

Bepaal de tweede orde gedeeltelijke derivaten:  ∂_Xxf, ∂_Yyf, ∂_YxF En ∂_XYF Voor dezelfde functie F van voorbeeld 1.

Procedure

In dit geval, aangezien de eerste gedeeltelijke derivaat al is berekend in X En En (Zie Voorbeeld 1):

∂_XxF = ∂_X(∂_Xf) = ∂_X(-6x) = -6

∂_YyF = ∂_En(∂_Enf) = ∂_En(4y - 12) = 4

∂_YxF = ∂_En(∂_Xf) = ∂_En(-6x) = 0

∂_XYF = ∂_X(∂_Enf) = ∂_X(4y - 12) = 0

Dat wordt waargenomen ∂_YxF = ∂_XYF, Zo vervullen de stelling van Schwarz, sinds de functie F en de eerste -orde gedeeltelijke derivaten zijn allemaal continue functies in R².

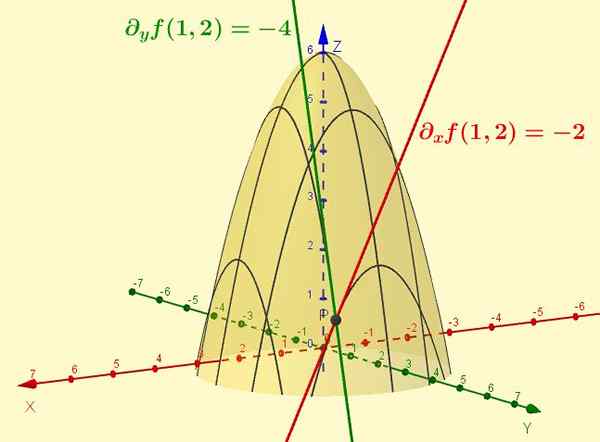
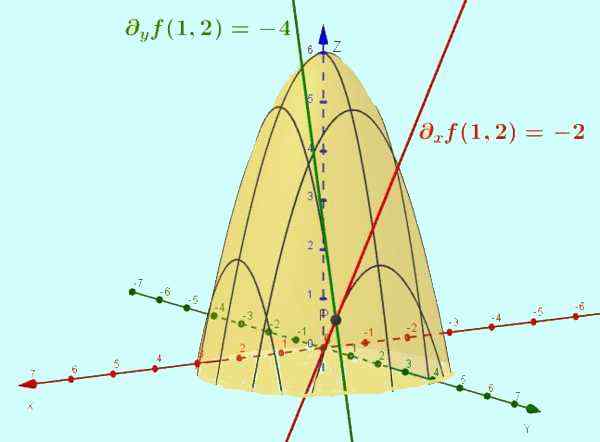Figuur 2. De functie z = f (x, y) = -x2 - y2 + 6 is het oppervlak dat in de figuur wordt getoond. De gedeeltelijke afgeleide met betrekking tot X is de helling van de raaklijn van de curve die het gevolg is van de kruising van genoemde oppervlak met het vlak Y = CTTE (het specifieke geval wordt getoond y = 2). Evenzo is het deel van F ten opzichte van en is de helling van de raaklijn van de kruising met x = 1, op het punt (1, 2, 1).

Opgeloste oefeningen

Oefening 1

Wees de functie:

Kan u van dienst zijn: kwadratische opvolgingen: voorbeelden, regel en oefeningen opgelost

f (x, y) = -x² - En² + 6

Vind functies G (x, y) = ∂_XF  En H (x, y) = ∂_EnF.

Oplossing

De gedeeltelijke afgeleide van F met betrekking tot X, waarvoor de variabele En Het wordt constant:

G (x, y) = - 2x

Evenzo de gedeeltelijke afgeleide van G met betrekking tot En, aan het doen X constant, resulterend voor de functie H:

H (x, y) = -2Y

Oefening 2 

Evalueer voor het punt (1, 2) De functies F (x, y) En G (x, y) van oefening 1. Interpreteer de resultaten.

Oplossing

Waarden worden vervangen x = 1 En y = 2 het verkrijgen van:

F (1,2) = -(1)² -(2)² + 6 = -5 + 6 = 1

Dit is de waarde die de functie f neemt wanneer op dat moment wordt geëvalueerd.

De functie F (x, y) Het is een twee -dimensionaal oppervlak en coördineren z = f (x, y) Het is de hoogte van de functie voor elk paar (X, y). Wanneer het paar wordt ingenomen (1.2), De oppervlaktehoogte F (x, y) is Z = 1.

De functie G (x, y) = - 2x vertegenwoordigt een vlak in de drie -dimensionale ruimte waarvan de vergelijking is Z = -2x O goed -2x + 0 en -z = 0.

Dit vlak staat loodrecht op het vlak XZ En ga door het punt (0, 0, 0). Wanneer geëvalueerd in x = 1 En y = 2 Dus Z = -2. Merk op dat de waarde z = g (x, y) Het is onafhankelijk van de waarde die is toegewezen aan de variabele En.

Aan de andere kant, als het oppervlak kruist F (x, y) Met het vliegtuig y = c, met C constant, je hebt een curve in het vliegtuig Zx: z = -x² - C² + 6.

In dit geval de afgeleide van Z met betrekking tot X valt samen met de gedeeltelijke afgeleide van F (x, y) met betrekking tot X: D_X Z = ∂_XF .

Bij het evalueren in het paar (x = 1, y = 2) De gedeeltelijke afgeleide op dat moment ∂_XF (1.2) Het wordt geïnterpreteerd als de helling van de lijn die op de curve raakt z = -x² + 2 op het punt (x = 1, y = 2) En de waarde van deze helling is -2.

Referenties

1. Ayres, f. 20000000000000000000. Berekening. 5ed. MC Graw Hill.
2. Gedeeltelijke derivaten van een functie in verschillende variabelen. Hersteld van: gebouw.UPM.is.
3. Leithold, l. 1992. Berekening met analytische geometrie. Harla, s.NAAR.
4. Purcell, E. J., Varberg, D., & Rigdon, s. EN. (2007). Berekening. Mexico: Pearson Education.
5. Gorostizaga J. C. Gedeeltelijke derivaten. Hersteld van: ehu.EUS
6. Wikipedia. Gedeeltelijke afgeleide. Hersteld van: is.Wikipedia.com.