Decodering van uitdrukkingen
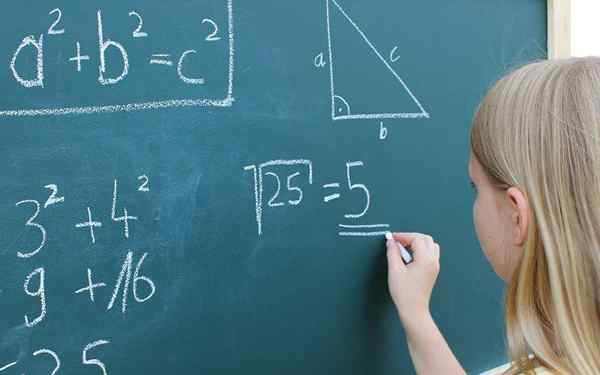
- 4861
- 39
- James Dach
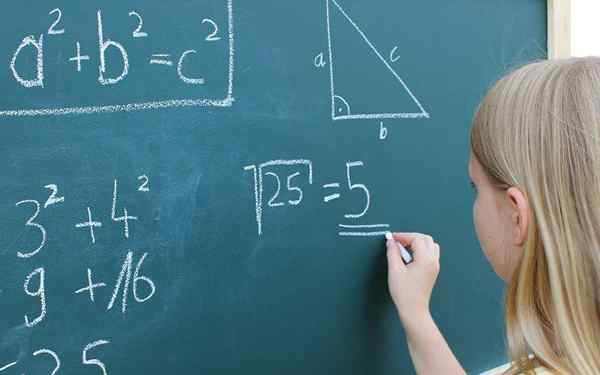 Wiskundige uitdrukkingen. Met licentie
Wiskundige uitdrukkingen. Met licentie Wat is het decoderen van uitdrukkingen?
De Decodering van uitdrukkingen Het verwijst naar de manier om verbaal een wiskundige uitdrukking te uitdrukken. In wiskunde, een uitdrukking, Ook wel wiskundige expressie genoemd, het is een combinatie van letterlijke coëfficiënten en letterlijke delen door andere wiskundige tekens (+, -, x, ±, /, [],), om een wiskundige bewerking te vormen.
In eenvoudigere woorden worden de coëfficiënten weergegeven door getallen, terwijl het letterlijke deel bestaat uit letters (de eerste drie letters van het alfabet, A, B en C, worden meestal gebruikt om het letterlijke onderdeel aan te duiden).
Op hun beurt vertegenwoordigen deze "letters" magnitudes, variabelen en constanten waaraan een numerieke waarde kan worden toegewezen.
Wiskundige uitdrukkingen bestaan uit termen, die elk van de elementen zijn die worden gescheiden door operatiesymbolen. De volgende wiskundige uitdrukking heeft bijvoorbeeld vier termen:
5x2 + 10x + 2x + 4
Opgemerkt moet worden dat uitdrukkingen alleen kunnen worden gevormd door coëfficiënten, door coëfficiënten en letterlijke onderdelen en alleen door letterlijke delen.
Bijvoorbeeld:
25 + 12
2x + 2y (algebraïsche expressie)
3x + 4/y + 3 (irrationele algebraïsche expressie)
x + y (hele algebraïsche expressie)
4x + 2y2 (hele algebraïsche expressie)
Decodering van wiskundige uitdrukkingen
Decodering van eenvoudige wiskundige uitdrukkingen
1. A + B: de som van twee getallen
Bijvoorbeeld: 2 + 2: de som van twee en twee
2. A + B + C: de som van drie getallen
Bijvoorbeeld: 1 + 2 + 3: de som van één, twee en drie
3. A - B: de aftrekking (of het verschil) van twee getallen
Bijvoorbeeld: 2 - 2: de aftrekking (of verschil) van twee en twee
4. A X B: het product van twee nummers
Kan u van dienst zijn: probleembenaderingBijvoorbeeld: 2 x 2: het product van twee en twee
5. naar ÷ B: De twee getallenverhouding
Bijvoorbeeld: 2/2: het quotiënt van twee en twee
6. 2 (x): twee keer per nummer
Bijvoorbeeld: 2 (23): tweemaal 23
7. 3 (x): drievoudige van een nummer
Bijvoorbeeld: 3 (23): The Triple of 23
8. 2 (a + b): tweemaal de som van twee getallen
Bijvoorbeeld: 2 (5 + 3): tweemaal de som van vijf en drie
9. 3 (a + b + c): drievoudige van de som van drie getallen
Bijvoorbeeld: 3 (1 + 2 + 3): drievoudige van de som van één, twee en drie
10. 2 (a - b): tweemaal het verschil van twee getallen
Bijvoorbeeld: 2 (1 - 2): tweemaal het verschil van één en twee
elf. x/2: de helft van een nummer
Bijvoorbeeld: 4/2: de helft van vier
12. 2n + x: de som van dubbel één nummer en een ander nummer
Bijvoorbeeld: 2 (3) + 5: de som van dubbele drie en vijf
13. X> y: "equis" is groter dan "ye"
Bijvoorbeeld: 3> 1: drie is groter dan één
14. X < y: “Equis” es menor que “ye”
Bijvoorbeeld: 1 < 3: Uno es menor que tres
vijftien. X = y: "equis" is gelijk aan "ye"
Bijvoorbeeld: 2 x 2 = 4: het product van twee en twee is gelijk aan vier
16. X2 : Het vierkant van een nummer of een vierkant nummer
Bijvoorbeeld: 52 : Het vijf of vijf vierkante vierkant
17. X3: De kubus van een nummer of een nummer naar de kubus
Bijvoorbeeld: 53: De vijf of vijf kubus naar de kubus
Kan u van dienst zijn: kwalitatieve methode18. (A + B)2: Het vierkant van de som van twee getallen
Bijvoorbeeld: (1 + 2)2: Het vierkant van de som van één en twee
19. (x - y)/2: de helft van het verschil van twee getallen
Bijvoorbeeld: (2 - 5)/2: de helft van het verschil van twee en vijf
twintig. 3 (x + y)2: Drievoud van het kwadraat van de som van twee getallen
Bijvoorbeeld: 3 (2 + 5)2 : Het drievoudige vierkant van de som van twee en vijf
eenentwintig. (A + B)/2: twee nummers
Bijvoorbeeld: (2 + 5)/2: de twee -en vijf semi -seismum
Decodering van algebraïsche uitdrukkingen
1. 2 x5 + 7/y + 9: [Twee equis verhoogd tot vijf] meer [zeven over ye] meer [negen]
2. 9 x + 7y + 3 x6 - 8 x3 + 4 y: [Negen equis] meer [zeven jaar] meer [drie equis verhoogd tot zes] minder [acht equis verhoogd tot 3] meer [vier jaar]
3. 2x + 2y: [twee equis] meer [twee jaar]
4. X/2 - Y5 + 4y5 + 2x2: [x op 2] minder [en verhoogd tot vijf] meer [vier en verhoogd tot vijf] meer [twee vierkante verhoogde]
5. 5/2 x + y2 + X: [vijf op twee equis] meer [en kwadrated] Meer [equis]
Polynoomdecodering
1. 2x4 + 3x3 + 5x2 + 8x + 3: [twee van equis verhoogd tot de vier] meer [drie van equis verheven tot de drie] meer [vijf van de vierkante verhoogde] meer [8 van equis] plus drie
2. 13 en6 + 7y4 + 9y3 + 5Y: [Dertien van en verheven tot zes] meer [zeven van en verheven tot de vier] meer [negen van en verheven tot de drie] meer [vijf van ye]]
3. 12Z8 - 5z6 + 7z5 + Z4 - 4Z3 + 3z2 + 9z: [Twaalf Zeta verheven tot acht] minder [vijf van Zeta verheven tot zes] meer [zeven van Zeta verheven tot vijf] meer [zeta verheven tot vier] minus [vier van zeta verheven tot de kubus] meer [drie van Zeta verheven tot het vierkant] meer [negen Zeta]
Het kan u van dienst zijn: het belang van wiskunde om fysieke situaties aan te pakkenReferenties
- Wrinting -uitdrukkingen met variabelen. Hersteld van Khanacademy.borg.
- Begrip van algebraïsche uitdrukkingen door ervaren gebruikers van wiskunde. NCBI hersteld.NLM.NIH.Gov.
- Wiskundige uitdrukkingen schrijven. Hersteld van Mathgoodies.com.

