Regelmatige, onregelmatige decagon, eigenschappen, voorbeelden

Hij decagon Het is een platte figuur met een polygoonvormige van 10 zijden en 10 hoekpunten of tips. De ontcagons kunnen regelmatig of onregelmatig zijn, in het eerste geval hebben alle partijen en interne hoeken dezelfde maatregel, terwijl in de tweede de zijkanten en/of de hoeken van elkaar verschillen.

Figuur 1 toont voorbeelden van decagons van elk type en zoals we kunnen zien, is de reguliere decagon erg symmetrisch.

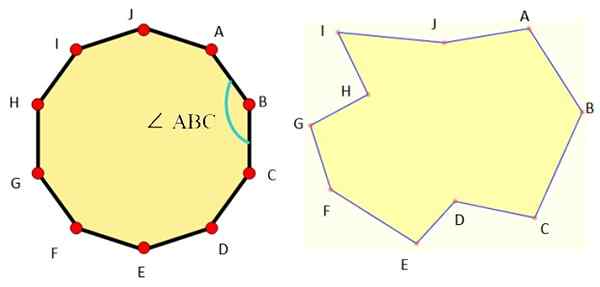Figuur 1. Links een normale decagon en rechts een onregelmatige decagon. Bron: Wikimedia Commons/F. Zapata/Mathpenref.

De basiselementen van alle decagon zijn:

-Kanten, de lijnsegmenten die bij het toetreden tot de Decagon.

-Hoekpunten of punten tussen elke opeenvolgende kant.

-Interne en externe hoeken tussen aangrenzende kanten.

-Diagonalen, segmenten die twee niet -opeenvolgende hoekpunten verenigen.

De hoekpunten worden door hoofdletters genoemd, zoals weergegeven in figuur 1, waar de eerste letters van het alfabet werden gebruikt, maar elke letter kan worden gebruikt.

De zijkanten worden gesymboliseerd met de twee letters van de hoekpunten waaronder, bijvoorbeeld de AB -zijde is die tussen de hoekpunten A en B. Op dezelfde manier wordt het gedaan met de diagonalen, dus we hebben de diagonale AF, die lid wordt van punten a en f.

Voor hoeken gebruiken we dit symbool: ∠, vergelijkbaar met een hellende l. De hoek ∠ ABC is bijvoorbeeld een wiens hoekpunt B is en waarvan de zijkanten de AB- en BC -segmenten zijn.

[TOC]

Regelmatige decagon

In de reguliere decagon hebben alle partijen dezelfde maatregel, evenals interne hoeken. Daarom wordt gezegd dat het zo is gelijkzijdig (gelijke zijden) en gelijkhoekig (Gelijke hoeken). Het is een zeer symmetrische figuur

Interieurhoeken van een reguliere decagon

Om de maat voor de interne hoeken van een gewone polygoon te vinden, inclusief de reguliere decagon, wordt de volgende formule gebruikt:

Waar:

-Ik is de maat voor de hoek in graden.

-n is het aantal zijden van de polygoon. In het geval van decagon n = 10.

Kan je van dienst zijn: heptagon

N = 10 vervangen in de vorige formule verkrijgen we het volgende:

Nu wordt gezegd dat een polygoon is convex Als de hoekige maatregelen minder zijn dan 180º, is de polygoon anders concaaf. Zoals elke interne hoek van de reguliere decagon meet 144º en is minder dan 180º, dan is het een convexe polygoon.

Som van interne hoeken

De som van de maatregelen van de interne hoeken van elke polygoon is in graden:

S = (N-2) x 180º; n is altijd groter dan 2

In deze formule moeten we:

-S is de som van de maatregelen van de interne hoeken.

-n is het aantal zijden. Voor de decagon n = 10

De formule toepassen voor n = 10 resultaten:

S = (10 - 2) x 180º = 1440º

Buitenhoeken 

Een buitenste hoek wordt gevormd tussen één kant en de uitbreiding van de aangrenzende kant, laten we eens kijken:

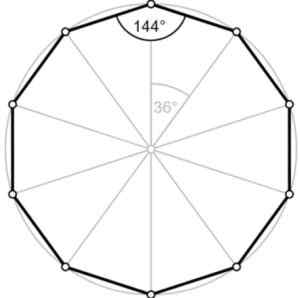
Figuur 2.- De externe hoek van de reguliere decagon meet 36º. Fontein. Wikimedia commons/f. Zapata.

De hoek ∠ ABC plus de externe hoek voegt 180º toe, dat wil zeggen dat ze zijn Aanvullend. Daarom is de externe hoek gelijk aan 180º-144º = 36º, zoals we in de figuur zien.

Aantal diagonalen

Zoals eerder vermeld, zijn de diagonalen de segmenten die niet -opeenvolgende hoekpunten verenigen. Hoeveel diagonalen kunnen we traceren in een decagon? Wanneer het aantal hoekpunten klein is, kunnen ze gemakkelijk worden geteld, maar wanneer dat aantal toeneemt, kunt u een account verliezen.

Gelukkig is er een formule om het aantal diagonalen te kennen dat een polygoon heeft N zijkanten:

Voor de decagon vervangen we n = 10 en krijgen we:

D = 10 x (10 - 3) /2 = 35

In de reguliere decagon worden alle diagonalen op een bepaald punt gesneden, wat het midden van de figuur is:

figuur 3. Hoeken en diagonalen van de reguliere decagon. Bron: Wikimedia Commons.

Centrum

Het midden van een polygoon wordt gedefinieerd als dat op gelijke afstand van een hoekpunt. In de vorige figuur valt het centrum samen met het snijpunt van alle diagonalen.

Omtrek

Als de reguliere Decagon zijde A heeft, is de omtrek P de som van alle kanten:

Kan u van dienst zijn: 90 divisors: wat zijn en uitleg

P = 10.naar

Gebied

De lengte kennen naar Aan de zijkant wordt het reguliere decagongebied berekend door:

Een geschatte formule voor het gebied is:

En een derde optie om het gebied te vinden is over de lengte van de apothem l_NAAR. Dit is het segment dat aan de ene kant het middelpunt aansluit bij het midden van de polygoon.

In dit geval kan het gebied worden berekend met behulp van de formule:

Onregelmatige decagon

De onregelmatige decagon is niet gelijkzijdig of Equiaggle, en in het algemeen mist het de symmetrie van de reguliere figuur, hoewel sommige decagons mogelijk symmetrie hebben.

Ze kunnen ook convex of concaaf zijn, als er interne hoeken zijn groter dan 180º.

De onregelmatige decagon van figuur 1 is concaaf, omdat sommige van zijn interne hoeken groter zijn dan 180º. Het is duidelijk dat er veel combinaties van hoeken en partijen zijn die aanleiding geven tot een onregelmatige decagon.

In elk geval is het vervuld dat:

-De interne hoeken van een onregelmatige decagon voegt ook 1440º toe.

-Het heeft ook 35 diagonalen.

Gebied van een onregelmatige decagon door Gauss -determinanten

Over het algemeen is er geen unieke formule om het gebied van een onregelmatige polygoon te vinden, omdat de zijkanten en hoeken anders zijn. U kunt echter het kennen van de coördinaten van de hoekpunten vinden en de Gauss -determinanten:

-Laten we bellen (x_N , En_N ) naar de coördinaten van de hoekpunten, met N variërend van 1 tot 10.

-U kunt beginnen met elk hoekpunt, waaraan coördinaten worden toegewezen (x x₁, En₁ )). Nu moet u de waarden van elke coördinaat in deze formule vervangen:

Waar determinanten precies de bewerkingen zijn tussen haakjes.

-Het is belangrijk om op te merken dat de laatste determinant het eerste hoekpunt omvat samen met de laatste. Voor de Decagon zou het zo zijn:

(X₁₀En₁ - X₁En₁₀))

Kan u van dienst zijn: lagrange interpolatie

Belangrijk: De balken zijn die van absolute waarde en betekenen dat het eindresultaat altijd met een positief teken is.

De procedure kan moeizaam zijn wanneer de figuur veel hoekpunten heeft, in het geval van de decagon zijn er 10 bewerkingen, dus het is raadzaam om een ​​tabel of een lijst te maken.

Oefening opgelost

Bereken het onregelmatige decagongebied dat in de figuur wordt getoond. De coördinaten van de hoekpunten zijn a, b, c ... j, wiens waarden links worden getoond.

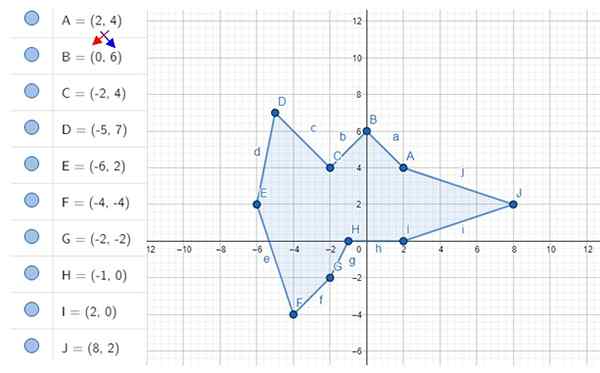Figuur 4. Onregelmatige decagon en zijn hoekpunten. Bron: f. Zapata met Geogebra.

Oplossing

-We maken elk van de 10 bewerkingen:

• 2 × 6 - 4 × 0 = 12 - 0 = 12
• 0 × 4 - 6 × (-2) = 0 + 12 = 12
• (-2) × 7- 4 × (-5) = -14 + 20 = 6
• (-5) × 2 -7 × (-6) = -10 + 42 = 32
• (-6) × (-4) -2 × (-4) = 24 + 8 = 32
• (-4) × (-2)-(-4) × (-2) = 8-8 = 0
• (-2) × 0-(-2) × (-1) = 0 -2
• (-1) × 0 - 0 × (2) = 0 - 0 = 0
• 2 × 2 - 0 × 8 = 4 - 0 = 4
• 8 × 4 -2 × 2 = 32 - 4 = 28

-We voegen de resultaten toe:

12 + 12 + 6 + 32 + 32 + 0 + (-2) + 0 + 4 + 28 = 124

Een positief resultaat wordt zelfs verkregen, zelfs zonder de staven van absolute waarde, maar als het negatief is, wordt hetzelfde gewijzigd.

-Het vorige resultaat wordt gedeeld door 2 en dat is het gebied van de polygoon:

A = 124/2 = 62

Decangon -eigenschappen

Hieronder is de samenvatting van de algemene eigenschappen van een decagon, nu regelmatig of onregelmatig:

-Heeft 10 zijden en 10 hoekpunten.

-De som van interne hoeken is 1440º.

-Er zijn 35 diagonalen.

-De perimeter is de som van alle kanten.

-U kunt driehoeken maken in een polygoontekensegmenten van een hoekpunt naar alle anderen. In een decagon is het mogelijk om 8 driehoeken op deze manier te tekenen, zoals hieronder getoond:

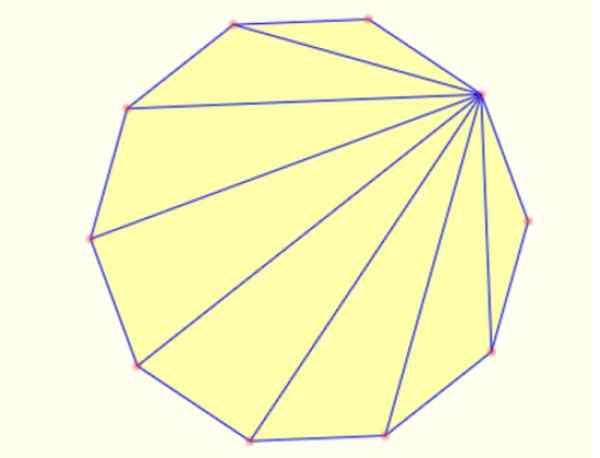Figuur 5. Interne driehoeken in een reguliere decagon. Bron: Mathpenref.

Referenties

1. Alexander, D. 2013. Geometrie. 5e. Editie. Cengage leren.
2. Decagon.com. Decagon. Hersteld van: Decagon.com
3. Math Open Referentie. Decagon. Hersteld van: Mathpenref.com.
4. Sangaku -wiskunde. Elementen van een polygoon en zijn classificatie. Hersteld van: Sangakoo.com.
5. Wikipedia. Decagon. Hersteld van: is.Wikipedia.com.