Wat zijn de delers van 30? (Uitleg)
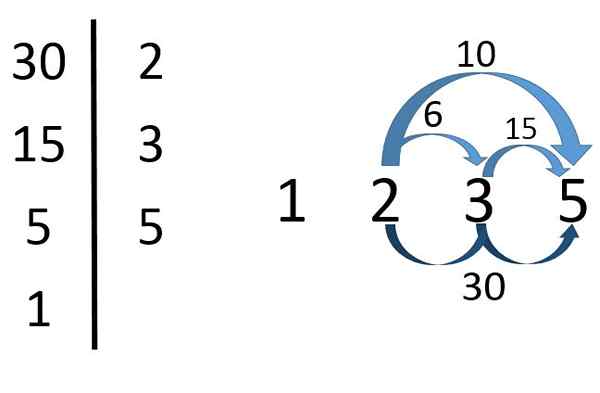
- 3587
- 227
- Cecil Graham
De divisors van 30 zijn 1, 2, 3, 5, 6, 10, 15 en 30. We leggen uit waarom en hoe u het zelf kunt berekenen.
Kan snel bekend zijn Wat zijn de delers van 30, evenals elk ander nummer (anders dan nul), maar het fundamentele idee is om te leren hoe divisors van een getal op een algemene manier worden berekend.
Er moet voorzichtig zijn wanneer u over divisors praat, omdat snel kan worden vastgesteld dat alle divisors van 30 1, 2, 5, 6, 10, 15 en 30 zijn, maar hoe zit het met de negatieven van deze cijfers? Zijn divisors of niet?
Om de vorige vraag te beantwoorden, is het noodzakelijk om een zeer belangrijke term in de wiskundewereld te begrijpen: het divisie -algoritme.
Divisie -algoritme
Het divisie -algoritme (of Euclidian Division) zegt het volgende: Gegeven twee gehele getallen "N" en "B", "B" anders dan nul (b ≠ 0), er zijn unieke "Q" en "R", zodat n = BQ+R, waar 0 ≤ r < |b|.
Het nummer "n" wordt dividend genoemd, "b" wordt divisor genoemd, "q" wordt quotiënt genoemd en "r" wordt de rest of afval genoemd. Wanneer de rest "R" gelijk is aan 0, wordt gezegd dat "B" "N" verdeelt, en dit wordt aangeduid met "B | N".
Het divisie -algoritme is niet beperkt tot positieve waarden. Daarom kan een negatief getal een deler zijn van een ander nummer.
Waarom 7.5 geen deler van 30 is?
Met behulp van het divisie -algoritme is te zien dat 30 = 7,5 × 4+0. De rest is gelijk aan nul, maar er kan niet worden gezegd dat 7,5 30 verdeelt.
Kan u van dienst zijn: exponentiële functie: eigenschappen, voorbeelden, oefeningenDivisors van 30
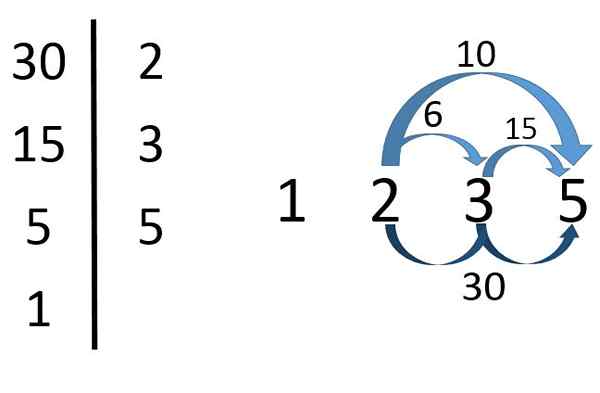 Divisors van 30
Divisors van 30 Zoals in het beeld te zien is, moeten eerst hun prime factoren worden gevonden om de divisors van 30 te vinden.
Dan, 30 = 2x3x5. Vanaf hier wordt geconcludeerd dat 2, 3 en 5 Ze zijn divisors van 30. Maar dat geldt ook voor de producten van deze belangrijkste factoren.
Zodat 2 × 3 =6, 2 × 5 =10, 3 × 5 =vijftien en 2x3x5 =30 Ze zijn divisors van 30. Hij 1 Het is ook een deler van 30 (hoewel het in werkelijkheid een deler van elk getal is).
Dat kan worden geconcludeerd 1, 2, 3, 5, 6, 10, 15 en 30 zijn divisors van 30 (Iedereen vervult het divisie -algoritme), maar we moeten niet vergeten dat hun negatieven ook delers zijn.
Daarom zijn alle delers van 30: -30, -15, -10, -6, -5, -3, -2, -1, 1, 2, 3, 5, 6, 10, 15 en 30.
Wat hierboven is geleerd, kan worden toegepast met elk heel nummer.
Als u bijvoorbeeld de divisors van 92 wilt berekenen, gaat u verder zoals voorheen. Het breekt af als een product van priemgetallen.
92 wordt gedeeld door 2 en verkregen 46; Nu is 46 opnieuw gedeeld door 2 en krijgt 23.
Dit laatste resultaat is een priemgetal, dus het zal niet meer divisors hebben naast 1 en dezelfde 23.
We kunnen dan 92 = 2x2x23 schrijven. Doorgaan zoals eerder, wordt geconcludeerd dat 1,2,46 en 92 92 divisors zijn.
Ten slotte zijn de negatieven van deze cijfers op de vorige lijst opgenomen, wat de lijst is van alle divisors van 92 is -92, -46, -4, -2, -1, 1, 2, 4, 46, 46, 92.
- « Activiteiten voor kinderen met leerproblemen
- Hoeveel honderdsten passen in een tiende? (Voorbeelden) »

