Rigide lichaam

Wat is een rigide lichaam?

Een rigide lichaam is een materieel object waarvan de deeltjes altijd in dezelfde relatieve posities blijven. Daarom is het een object dat niet is vervormd, een kwaliteit die wordt toegeschreven aan de intense cohesiekrachten die de deeltjes op hun plaats houden.

Eigenlijk hebben de deeltjes van elk lichaam dat wordt onderworpen aan externe krachten, neigen om te trillen of te bewegen, dus het object is altijd tot op zekere hoogte vervormen, maar deze effecten zijn meestal klein.

Wanneer dit het geval is, kan worden aangenomen dat het lichaam rigide is en een zeer goede benadering van zijn gedrag heeft, zelfs als het een idealisatie is.

Rigide lichamen typen

U kunt twee soorten rigide lichaam onderscheiden:

• Degenen wier deeltjes in discrete hoeveelheden komen, dat wil zeggen dat ze kunnen tellen. Twee metalen bollen verbonden door een dunne en lichte staaf kunnen bijvoorbeeld worden beschouwd als een unieke entiteit. Als de staaf stijf genoeg is om niet te buigen, wordt het systeem beschouwd als een rigide lichaam.
• Degenen die continu zijn, wat betekent dat de deeltjes die ze verzinnen niet te onderscheiden zijn. Elke dag en natuurobjecten zijn goede voorbeelden: stenen, meubels en anderen, evenals het land en andere hemelse rotsen rocky.

Rigide lichaamsbeweging en dynamiek

Net als objecten die als deeltjes worden beschouwd, kunnen rigide lichamen worden overgedragen, roteren en een meer algemene beweging hebben, het combineren van vertaling en rotatie.

Om de vertaling te bestuderen is het niet nodig.

Deze vertaal- en rotatiebewegingen kunnen zijn:

• Onafhankelijk, zoals in het geval van de planeten, die een rotatiebeweging rond hun as hebben (beschouwd als gefixeerd) en een andere vertaling rond de zon, maar de snelheden van elk zijn niet gerelateerd.
• Broken-afval, als de hoeksnelheid en vertaalsnelheid van het massamiddelpunt zijn gerelateerd. In dit geval is de rotatieas mobiel, zoals in het geval van de cilinder die neerschieten zonder te glijden door een hellende helling.

Het kan u van dienst zijn: eerste wet van thermodynamica: formules, vergelijkingen, voorbeelden

De dynamiek van rigide vaste stof

De volgende magnitudes zijn relevant in de dynamiek van rigide vaste stof:

Massacentrum

Het massamiddelpunt is het punt waar de gehele massa van het lichaam wordt beschouwd als geconcentreerd. Als het een homogeen en symmetrisch lichaam is, als een bol, valt het centrum van massa samen met het geometrische centrum.

Het moment van traagheid

Deze scalaire grootte is de waarde van rotatie -traagheid of weerstand die zich verzet tegen een object om rond een bepaalde as te roteren. Het hangt volledig af van de geometrie van het object en de massa ervan en daarom is het in bepaalde gevallen gemakkelijker om bepaalde assen om te keren dan op andere.

Voor lichamen met goed gedefinieerde geometrische vormen zijn er tafels met de traagheidsmomenten met betrekking tot de symmetriezen, bijvoorbeeld degene die door het massacentrum gaat. Met deze informatie en de stellingen gerelateerd aan het traagheidsmoment, kunnen de momenten met betrekking tot andere assen gemakkelijk worden berekend.

Krachten en koppel of koppel

Krachten zijn nodig om een ​​lichaam te verplaatsen. Als het rigide vaste massacentrum beweegt, is de bewegingsvergelijking, volgens de tweede wet van Newton,:

F_Netto = M ∙naar_cm

Waar:

-De netto kracht is F_Netto

-M is de massa

-De versnelling van het massacentrum is naar_cm

Maar niet alle toegepaste krachten doen het object breken. Om dit te doen is het koppel of het koppel nodig, wat zegt hoe effectief het de rotatie -werking van een kracht is. Het wordt gedefinieerd als het vectorproduct tussen de positievector R Met betrekking tot een bepaald punt en kracht F in kwestie. Het wordt aangeduid met de Griekse brief τ (Vetgedrukte brief is het ook een vector):

Kan u van dienst zijn: elliptische beweging

τ = R × F

In het internationale systeem is de koppeleenheid N⋅m (Newton per meter).

In veel gevallen wordt de rotatiebeweging rond een as die door het massamiddelpunt passeert, beschreven door een analoge vergelijking met de tweede wet van Newton:

Waar de subscript "Z" verwijst naar de rotatieas die door een as van symmetrie gaat, vast of bewegend, maar zonder van richting te veranderen, en_cm Het is het moment van traagheid ten opzichte van het midden van massa en α_Z Het is de hoekversnelling van het lichaam. De zomer bedekt alle externe momenten rond de Z -as.

Kinetische energie van een rigide vaste stof

De beweging van een rigide lichaam wordt beschreven door vertalingen van het midden van massa en rotaties rond dat punt, daarom heeft de kinetische energie beide bijdragen.

Laat K de kinetische energie van het lichaam, v_cm De snelheid van het massacentrum, de massa van het lichaam, en_cm Het traagheidsmoment ten opzichte van het massamidrum en ω de hoeksnelheid. Het kan worden aangetoond dat kinetische energie is:

K = ½ mV_cm² + ½ i_cm Ω²

Opgemerkt wordt dat de tweede term rechts de rotatie -analoog is van de term van links. Daar speelt het traagheidsmoment dezelfde rol als de massa, terwijl de hoeksnelheid dezelfde rol speelt als de lineaire snelheid.

Voorbeelden in het dagelijks leven

Fysieke slinger

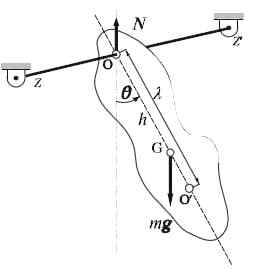Fysieke slinger

De fysieke slinger of echte slinger is heel gemakkelijk te bouwen: het bestaat uit een stijve vaste stof zoals een staaf of stang, die vrij rond een horizontale as oscilleert. De rotatieas kruist het massamiddelpunt van het object niet en dit kan in principe enige vorm hebben.

Kan u van dienst zijn: Weerstandsthermometer: kenmerken, werking, gebruik

Deze slinger verschilt van de eenvoudige slinger, omdat in deze laatste wordt beschouwd dat de massa die het componeert punctueel is.

Fietsenwiel

Fietsenwiel

Een ander goed bekend rigide lichaamsbeeld is het fietswiel, waarvan de as door het massamiddelpunt gaat, dat het midden van het wiel oversteekt. Zolang ze niet aan de zijkant of beurt leunen, zijn de vergelijkingen van de beschreven dynamiek van toepassing om uw beweging te beschrijven.

Een bowlingbal

Een goed voorbeeld van een rigide lichaam is de bowlingbal

Het stijve solide model past zich zeer goed aan om de beweging van de bowlingbal op het spoor te beschrijven of wanneer deze rolt zonder de retourhelling af te glijden.

De yoyo

YoYo is een populair speelgoed dat kan worden gemodelleerd als een rigide lichaam

Dit populaire speelgoed is gemaakt met een hout- of plastic cilinder en een touw overweldigd in een sleuf eromheen.

De cilinder kan worden gemodelleerd als een rigide lichaam waarin de spanning in de string het koppel voor de rotatie levert, terwijl het gewicht (toegepast op het massamiddelpunt) en de spanning verantwoordelijk is voor de verticale versnelling van het massamiddelpunt.

Referenties

1. Bauer, W. 2011. Fysica voor engineering en wetenschappen. Deel 1. MC Graw Hill. 
2. Giancoli, D.  2006. Fysica: principes met toepassingen. 6e. Ed Prentice Hall.
3.  Katz, D. 2013. Natuurkunde voor wetenschappers en ingenieurs. Stichtingen en verbindingen. Cengage leren.
4. Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14e. ED. Deel 1. Pearson.
5. Serway, r., Jewett, J. (2008). Natuurkunde voor wetenschap en engineering. Deel 1. 7e. ED. Cengage leren.