Criteria vergelijkbare driehoeken

Wat zijn de criteria van de driehoeken?

De criteria van de driehoeken zijn de regels die toestaan ​​te weten of twee driehoeken vergelijkbaar zijn. De gelijkenis van geometrische figuren, inclusief driehoeken, vereist dat de cijfers op dezelfde manier hebben, hoewel ze niet noodzakelijkerwijs dezelfde grootte of dezelfde oriëntatie hebben.

Voor twee driehoeken die vergelijkbaar zijn, is het noodzakelijk dat: i) hun homologe kanten evenredig zijn en ii) de interne hoeken van elk dezelfde maatregel hebben.

Figuur 1. Twee vergelijkbare driehoeken: hoewel ze niet dezelfde grootte hebben, zijn hun zijkanten evenredig en hebben hun interne hoeken gelijke maatregel. Bron: f. Zapata.

Een evenredige verhouding of verhouding tussen twee hoeveelheden A en B wordt weergegeven door de A/B -verhouding, met B ≠ 0. Voor soortgelijke driehoeken zijn de volgende verhoudingen tussen hun zijden geldig:

a/a '= b/b' = c/c '= r

De waarde van r wordt genoemd gelijkenis reden.

Bovendien moeten de overeenkomstige interne hoeken dus van dezelfde maat zijn, daarom: ∠a = ∠a '; ∠b = ∠b 'en ∠c = ∠c'. Volgens deze voorwaarden zijn de criteria van de Triangles -overeenkomst:

Criteria 1: Twee driehoeken zijn vergelijkbaar als ze twee interne hoeken van gelijke maatregelen hebben. Als dat zo is, meet de derde hoek ook hetzelfde, omdat de som van de interne hoeken in een driehoek 180º is:

α = α '; β = β '

Criteria 2: De driehoeken zijn vergelijkbaar als twee homologe kanten evenredig zijn en de hoek ertussen hetzelfde is:

a/a '= b/b'; α = α '

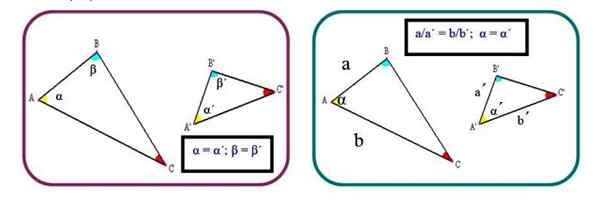Figuur 2. Twee criteria om de gelijkenis van driehoeken vast te stellen. Bron: f. Zapata.

Criteria 3: De drie homologe kanten zijn evenredig:

a/a '= b/b' = c/c '= r

Voorbeelden

De gelijkenis van driehoeken is zeer nuttig voor het berekenen van hoogten en afstanden die niet gemakkelijk direct meetbaar zijn. Door enkele eenvoudige berekeningen is het mogelijk om deze lengtes te achterhalen door vergelijkbare driehoeken te vergelijken.

Kan u van dienst zijn: Fundamentele stelling van rekenkunde: demonstratie, toepassingen, oefeningen

Hoogte van kolommen, gebouwen en bomen

Er wordt gezegd dat de vader van de geometrie in het oude Griekenland, zoals Miletus (625-547 tot.C.), berekende de hoogte van de kolom van een tempel zonder de noodzaak van speciale instrumenten, eenvoudigweg de lengte van de schaduw van de riet vergelijken met die van de kolom en de gelijkenis van driehoeken toepassen. Met dezelfde methode slaagde hij erin om de hoogte van de grote piramide van Egypte te meten en zo indruk te maken op de farao.

De afstand tot de maan

Er is een eenvoudig experiment dat wordt gedaan om de afstand tussen de aarde en de maan te berekenen. Het vereist een valuta, een beetje lijmband en een Vernier of een afgestudeerde regel. Wanneer de maan vol is, is de valuta bevestigd aan het glas van een raam en wordt de maan waargenomen met één oog, op een manier waarop de valuta alleen de volle maan bedekt.

Wanneer dit gebeurt, is de reden tussen de diameter van de valuta en de afstand tussen het oog en de valuta hetzelfde dat er is tussen de diameter van de maan en de afstand tussen het oog en de maan:

Valuta diameter/afstand valuta = maandiameter/afstand tot de maan

De reden is ongeveer 1/110. Wat betekent dat de afstand tot de maan 110 keer de diameter hiervan is.

Momenteel wordt de straal van de maan geschat in 1737.1 km, dus de diameter is 3474.2 km. Door deze waarde in de relatie te vervangen:

Afstand tot de maan = maandiameter ÷ (valutadiameter/afstand tot de valuta)

Is verkregen:

Afstand tot de maan = 3474.2 km ÷ (1/110) = 382.162 km

Het kan je van dienst zijn: hepagonaal prisma

Heel dicht bij de waarde vastgesteld door 384 astronomen.000 km.

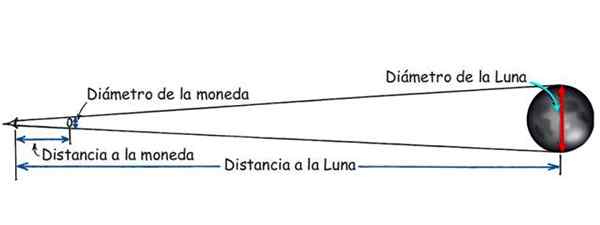figuur 3. De afstand tot de maan kan bekend zijn dankzij de gelijkenis van driehoeken. Bron: Modified Hewitt, P. Conceptuele fysica.

Afstand tussen een schip en de kust

Om de afstand tussen het schip en de kust te meten, zitten de palen vast op het strand in punten A, B, C en Q. ABC- en PCQ -driehoeken zijn vergelijkbaar met criteria 1, omdat ze twee gelijke hoeken hebben: de twee hoeken ∠c = α die worden tegengewerkt door het hoekpunt en de twee rechte hoeken gelijk aan 90º: ∠b = ∠q.

Er wordt gezegd dat twee driehoeken zich op deze manier bevinden Thales -positie En ze zijn altijd vergelijkbaar. Driehoeken worden geïdentificeerd in de positie van Thales voor het hebben van een gemeenschappelijke hoek en de tegenoverliggende zijden onder die hoek zijn parallel.

In de volgende sectie is er een oefening met numerieke waarden.

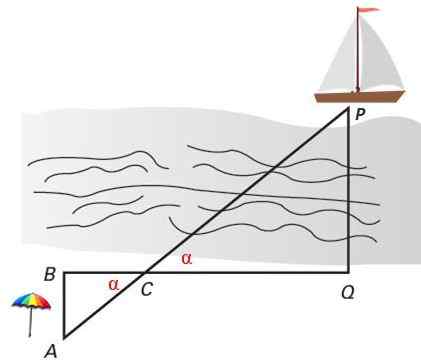Figuur 4. Twee vergelijkbare driehoeken in Thales -positie dienen om de loodrechte afstand van een schip naar de kust te berekenen. Bron: f. Zapata.

Opgeloste oefeningen

Oefening 1

U wilt ontdekken hoe ver de zeilboot verankerd is in de vorige figuur, vanaf een punt dat zich aan de oever van het strand bevindt, waarvoor staken worden genageld in punten A, B, C en Q, waardoor de driehoek ABC wordt bepaald, is vergelijkbaar met PCQ, maar waarvan de zijden gemakkelijker te meten zijn.

Bereken de loodrechte afstand PQ tussen het schip en de kust, door de gelijkenis van driehoeken, als de beschikbare afstanden zijn:

AB = 12 m

BC = 16 m

QC = 60 m

Oplossing

De verhoudingen tussen homologe kanten zijn:

Ab/qp = bc/cq = 16 m/60 m = 0.267

Daarom 0.267 is de reden voor gelijkenis:

AB/QP = 0.267

QP = AB / 0.267 = 12 m / 0.267 = 44.9 m

Oefening 2

In de volgende driehoek: hoeveel meet het AD -segment?

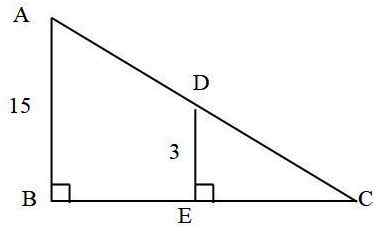
Het is bekend dat:

• AC = 25 cm
• AB = 15 cm
• DE = 3 cm

Kan u van dienst zijn: veelvouden van 2: wat zijn en uitleg

Oplossing

De driehoeken zijn vergelijkbaar, omdat ze een hoek delen die ∠c is en de zijkanten van en AB parallel zijn. De gelijkenisverhouding wordt berekend door:

R = AB / DE = 15 cm / 3 cm = 5

En ook door:

R = AC / DC

Daarom dc = ac / r = 25 cm / 5 = 5 cm

Sinds:

AC = AD + DC

Hieruit volgt dat AD = AC - DC = 25 cm - 5 cm = 20 cm

Oefening 3

Een gelijkbenige driehoek heeft een omtrek van 49 cm en een basis van 21 cm. Bereken de omtrek van een driehoek vergelijkbaar met deze, maar waarvan de basis 4 cm meet.

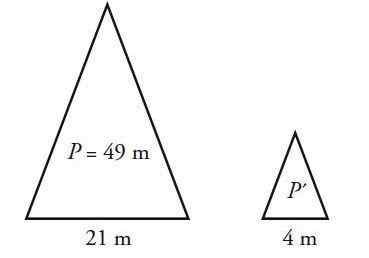
Oplossing

De gelijkbenige driehoek heeft twee gelijke zijden, anders dan basis B. Laat ℓ de maat van de zijkanten en P de omtrek, die bestaat uit de som van de drie zijden. Voor de grootste driehoek:

P = 2 ℓ + b = 49 cm

2 ℓ + 21 cm = 49 cm → ℓ = (49-21) cm / 2 = 14 cm

Nu wordt de verhouding tussen de zijkanten van de driehoeken verhoogd, die van de kleine driehoek worden gesymboliseerd met premies:

B/ b '= ℓ/ ℓ ℓ'

21 cm / 4cm = 14 cm / ℓ '→ ℓ ℓ' = 14 cm / (21 cm / 4 cm) = 2.67 cm

De omtrek van de kleine driehoek zal zijn:

P '= 2 ℓ' + b '= (2 x 2.67) cm + 4 cm = 9.33 cm.

Referenties

1. Alexander, D. 2013. Geometrie. 5e. Editie. Cengage leren.
2. Hewitt, Paul. 2012. Conceptuele fysieke wetenschap. 5e. ED. Pearson.
3. Clemens, s. Geometrie met toepassingen. Addison Wesley.
4. Ibáñez, p. 2010. Wiskunde III. Cengage leren.
5. Jiménez, r. Wiskunde II: Geometrie en trigonometrie. 2e. Editie. Pearson.
6. Stewart, J. 2007. Voorzetting. 5e. Editie. Cengage leren.
7. Vicmat. Samos Aristarco: Maatregelen voor zonnestelsels. Hersteld van: vicmat.com