Cilindrische coördinaten systeem, verandering en oefeningen

De cilindrische coördinaten Ze dienen om punten te vinden in de drie -dimensionale ruimte en bestaan ​​uit een radiale coördinaat ρ, een azimutale coördinaat φ en een hoogte -coördinaat Z.

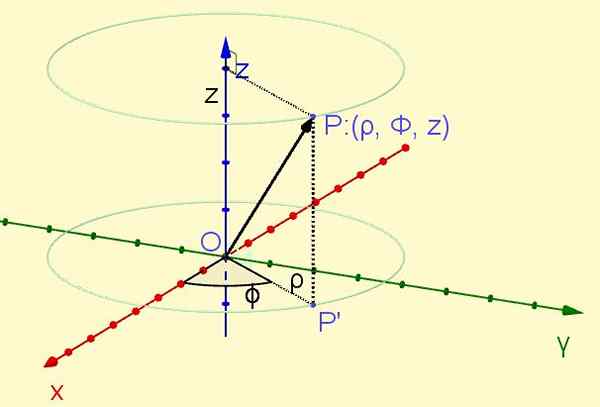
Een punt P Gelegen in de ruimte wordt orthogonaal op het vliegtuig geprojecteerd XY aanleiding geven tot het punt P ' In dat vliegtuig. De afstand van de oorsprong tot het punt P ' Definieert de coördinaat ρ, terwijl de hoek die de as vormt X Met de semi -strak OP ' Definieer de coördinaat φ. Eindelijk de coördinaat Z Het is de orthogonale projectie van het punt P op de as Z. (Zie figuur 1).

Figuur 1. Punt P van cilindrische coördinaten (ρ, φ, z). (Eigen uitwerking)

De radiale coördinaat ρ is altijd positief, de azimutale coördinaat φ varieert van nulradians tot twee Pi -radianen, terwijl de z -coördinaat elke echte waarde kan aannemen:

0 ≤ ρ < ∞

0 ≤ φ < 2π

- ∞ < z < + ∞

[TOC]

Verandering van coördinaten

Het is relatief eenvoudig om de Cartesiaanse coördinaten (x, y, z) te verkrijgen van een punt p van zijn cilindrische coördinaten (ρ, φ, z):

x = ρ cos (φ)

y = ρ sen (φ)

z = z

Maar het is ook mogelijk om de polaire coördinaten (ρ, φ, z) te verkrijgen op basis van de kennis van de Cartesiaanse coördinaten (x, y, z) van een punt p:

ρ = √ (x² + En²))

φ = arctan (y/x)

z = z

Vectorbasis in cilindrische coördinaten

De basis van cilindrische vectoren is gedefinieerd Uρ, Uφ, Uz.

De vector Uρ Het is raaklijn aan de lijn φ = ctte en z = ctte (radialiteit wijzen), de vector Uφ is raaklijn aan de lijn ρ = ctte en z = ctte en ten slotte Uz Het heeft dezelfde richting van de z -as.

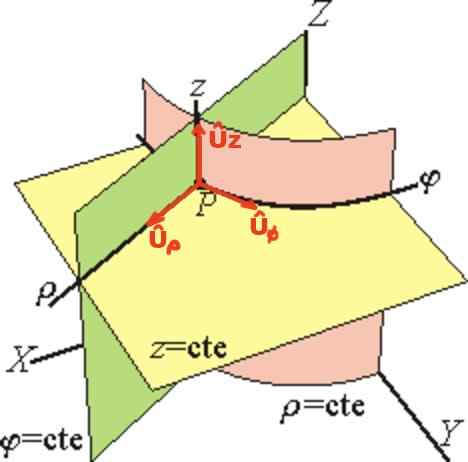Figuur 2. Cilindrische coördinaatbasis. (Wikimedia Commons)

In de cilindrische eenheidsbasis, de positievector R Vanuit een punt P is het vectoraal geschreven:

Het kan u van dienst zijn: domein en tegenspraak met een functie (met voorbeelden)

R = ρ Uρ + 0 Uφ + Z Uz

Aan de andere kant, een oneindigimale verplaatsing DR Uit punt P wordt het als volgt uitgedrukt:

DR = Dρ Uρ + ρ dφ  Uφ + Dz Uz

Evenzo is een oneindig element van DV -volume in cilindrische coördinaten:

Dv = ρ dρ dφ dz

Voorbeelden

Er zijn talloze voorbeelden van het gebruik en de toepassing van cilindrische coördinaten. In cartografie bijvoorbeeld de cilindrische projectie, precies gebaseerd op deze coördinaten. Er zijn meer voorbeelden:

voorbeeld 1

Cilindrische coördinaten hebben toepassingen in technologie. Als voorbeeld heeft u het CHS (cilinder-head-sector) -systeem van gegevenslocatie op een harde schijf, die eigenlijk uit verschillende schijven bestaat:

- De cilinder of baan komt overeen met coördineren ρ.

- De sector komt overeen met de φ -positie van het album dat op hoog roteert hoekige snelheid.

- De kop komt overeen met de z -positie van de leeskop op het bijbehorende album.

Elke informatie -byte heeft een nauwkeurig adres in cilindrische coördinaten (C, S, H).

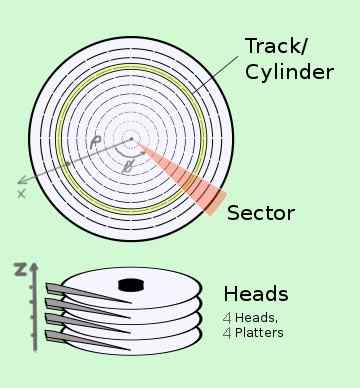Figuur 2. Locatie van informatie in cilindrische coördinaten in een hard schijfsysteem. (Wikimedia Commons)

Voorbeeld 2

Constructiekranen zetten de laadpositie in cilindrische coördinaten in. De horizontale positie wordt gedefinieerd door de afstand tot de kraanas of pijl. De verticale positie van de belasting wordt bepaald door de z -coördinaat van de hoogte.

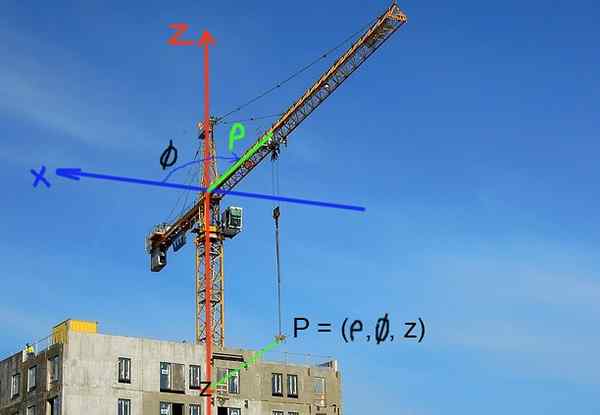figuur 3. De positie van de belasting in een bouwkraan kan gemakkelijk worden uitgedrukt in cilindrische coördinaten. (Pixabay -afbeelding - rcos r. Pérez)

Opgeloste oefeningen

Oefening 1

Er zijn de P1 -punten van cilindrische coördinaten (3, 120º, -4) en het punt P2 van cilindrische coördinaten (2, 90º, 5). Vind de Euclidiaanse afstand Tussen deze twee punten.

Kan u van dienst zijn: divisies waarin het residu 300 is

Oplossing: Eerst gaan we verder met het vinden van de Cartesiaanse coördinaten van elk punt na de formule die hierboven is opgetreden.

P1 = (3* cos 120º, 3* sen 120º, -4) = (-1.5, 2.60, -4)

P2 = (2* cos 90º, 2* sin 90º, 5) = (0, 2, 5)

De Euclidiaanse afstand tussen P1 en P2 is:

D (P1, P2) = √ ((0 - (-1.5)²+(2 - 2.60)²+(5 -(-4))² ) =…

… √ (2.25+0.36+81) = 9.14

Oefening 2

Punt P heeft Cartesiaanse coördinaten (-3, 4, 2). Zoek de overeenkomstige cilindrische coördinaten.

Oplossing: De cilindrische coördinaten worden gevonden met behulp van de hierboven gegeven relaties:

ρ = √ (x² + En²) = √ ((-3)² + 4²) = √ (9 + 16) = √ (25) = 5

φ = arctan (y/x) = arcan (4/(-3)) = -53.13º + 180º = 126.87º

Z = 2

Er moet aan worden herinnerd dat de arcangent -functie multivaluada is van periodiciteit 180º. Bovendien moet de hoek φ tot het tweede kwadrant behoren, omdat de x e y en van punt p -coördinaten in dat kwadrant zijn. Dit is de reden waarom 180º is toegevoegd aan het resultaat φ.

Oefening 3

Express in cilindrische coördinaten en in Cartesiaanse coördineert het oppervlak van een radiocilinder 2 en waarvan de as samenvalt met de Z -as.

Oplossing: het is wel verstaan ​​dat de cilinder een oneindige extensie in de Z -richting heeft, zodat de vergelijking van dit oppervlak in cilindrische coördinaten is:

ρ = 2

Om de Cartesiaanse vergelijking van het cilindrische oppervlak te verkrijgen, wordt het kwadraat van beide leden van de vorige vergelijking genomen:

ρ² = 4

We vermenigvuldigen met 1 beide leden van de vorige gelijkheid en passen de Fundamentele trigonometrische identiteit (Sen²(φ) + cos²(φ) = 1):

1 * ρ² = 1 * 4

(Sen²(φ) + cos²(φ)) * ρ² = 1 * 4

De haakjes ontwikkelt zich om te verkrijgen:

(ρ sen (φ))² + (ρ cos (φ))² = 4

Kan u van dienst zijn: populatie en steekproef

We herinneren ons dat de eerste haakjes (ρ sen (φ)) gecoördineerd is en een punt in polaire coördinaten, terwijl de haakjes (ρ cos (φ)) de x -coördinaat vertegenwoordigt, zodat we zijn vertrokken De cilindervergelijking in Cartesiaanse coördinaten:

En² + X² = 2²

De vorige vergelijking moet niet worden verward met die van een cirkel in het XY -vlak, omdat het in dit geval zo zou zijn: en² + X² = 2² ; Z = 0.

Oefening 4

Een straalcilinder r = 1 m en hoogte h = 1m heeft zijn radiaal verdeelde massa volgens de volgende vergelijking d (ρ) = c (1 - ρ/r) waarbij C een constante van waarde C = 1 kg/m is³. Zoek de totale massa van de cilinder in kilogram.

Oplossing: Het eerste is om te beseffen dat de functie d (ρ) de volumetrische masserdichtheid vertegenwoordigt en dat de dichtheidsmassa wordt verdeeld in cilindrische cascaronen van afnemende dichtheid van het midden tot de periferie. Een oneindigimaal volume -element volgens de symmetrie van het probleem is:

Dv = ρ dρ 2π h

Van daaruit moet je de oneindige massa van een cilindrische schaal zijn:

Dm = d (ρ) dv

Dus de totale massa van de cilinder zal door het volgende worden uitgedrukt Gedefinieerd integraal:

M = ∫_of^R D (ρ) dv = ∫_of^R C (1 - ρ/r) ρ dρ 2π h = 2π h c ∫_of^R (1 - ρ/r) ρ dρ

De oplossing van de aangegeven integrale is niet moeilijk te verkrijgen, het resultaat ervan:

∫_of^R (1 - ρ/r) ρ dρ = (⅙) r²

Het opnemen van dit resultaat in de expressie van de cilindermassa wordt verkregen:

M = 2π h c (⅙) r² = ⅓ π h c r² =

 ⅓ π 1m*1kg/m³* 1m² = π/3 kg ≈ 1.05 kg

Referenties

1. Arfken G en Weber H. (2012). Wiskundige methoden voor natuurkundigen. Een uitgebreide gids. 7e editie. Academische pers. ISBN 978-0-12-384654-9
2. CC -berekening. Opgeloste cilindrische en bolvormige coördinaten. Teruggewonnen uit: berekening.DC
3. Weisstein, Eric W. “Cilindrische coördinaten.”Van Mathworld-a Wolfram Web. Hersteld van: Mathworld.Wolfraam.com
4. Wikipedia. Cilindrisch coördinatensysteem. Opgehaald uit: in.Wikipedia.com
5. Wikipedia. Vectorvelden in cilindrische en bolvormige coördinaten. Opgehaald uit: in.Wikipedia.com