Constanten van antoine -formules, vergelijkingen, voorbeelden

De constanten van Antoine Er zijn drie parameters die verschijnen in een empirische relatie tussen verzadigingsdampdruk en temperatuur voor zuivere stoffen. Ze zijn afhankelijk van elke stof en worden verondersteld constant te zijn bij een bepaald bereik van temperaturen.

Uit dat bereik veranderen de constanten van Antoine hun waarde. De constanten zijn gerelateerd door een vergelijking die in 1888 is gecreëerd door de Franse ingenieur Louis Charles Antoine (1825-1897).

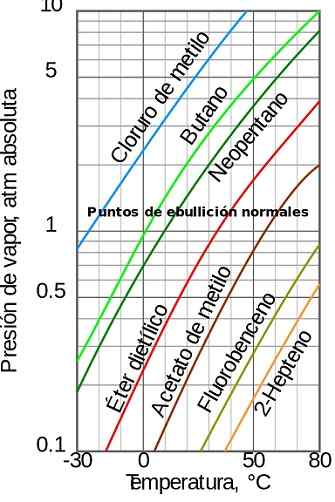
Figuur 1. Stoomdruk, afhankelijk van de temperatuur. Bron: Wikimedia Commons

[TOC]

Formules en vergelijkingen

De meest gebruikelijke manier om de functie van Antoine uit te drukken is:

 

In deze formule P vertegenwoordigt het de verzadigingsdampdruk die wordt uitgedrukt in kwikmillimeters (mmHg), t is de temperatuur die de onafhankelijke variabele is en tot expressie wordt gebracht in ℃. 

A, B en C zijn de constanten of parameters van de Antoine -formule.

Het belang van deze formule die ondanks het empirisch is, geeft een eenvoudige analytische uitdrukking die gemakkelijk kan worden gebruikt in thermodynamische berekeningen.

De formule van Antoine is niet uniek, er zijn meer precieze uitdrukkingen die uitbreidingen van deze formule zijn, maar met het nadeel dat zes of meer parameters heeft en hun wiskundige expressie complexer is, waardoor ze zeer praktijken kunnen gebruiken om te gebruiken in de thermodynamische berekeningen.

Verzadigingsdamp

Aangezien de formule van Antoine verzadigingsdampdruk meet, is het noodzakelijk om uit te leggen waar het uit bestaat.

In een glazen ampul of andere container wordt een vloeistof geplaatst. Alle luchtlucht wordt geëxtraheerd. De set wordt in een thermisch bad geplaatst totdat de balans is bereikt.

In het begin is alles vloeibaar, maar omdat er een vacuüm is, beginnen de snelste moleculen de vloeistof te verlaten die een gas vormt van dezelfde stof van de vloeistof.

Kan u van dienst zijn: uniforme rechtlijnige beweging: kenmerken, formules, oefeningen

Het vorige proces is het verdamping En naarmate de stoomdruk toeneemt. 

Sommige stoommoleculen verliezen energie en keren terug naar de vloeibare fase van de stof, dit is het proces van condensatie.

Dan komen twee processen, verdamping en condensatie tegelijkertijd op. Wanneer hetzelfde aantal vloeibare moleculen die erin zijn opgenomen, uitkomen, een dynamisch evenwicht En op dit moment treedt de maximale stoomdruk bekend als verzadigingsdruk op.

Het is deze dampverzadigingsdruk die de antoine -formule voor elke stof en elke temperatuur voorspelt.

In sommige vaste stoffen is er een soortgelijk fenomeen wanneer het rechtstreeks van de vaste fase naar de frisdrank gaat zonder de vloeibare fase te doorlopen, in deze gevallen kan een verzadigingsdampdruk ook worden gemeten.

Het is niet eenvoudig om een ​​theoretisch model vast te stellen dat begint bij vroege principes, omdat er veranderingen in moleculaire kinetische energie zijn, die van translationeel, rotatie- en vibratietype kunnen zijn, met de interne moleculaire bindingsergie. Het is om deze reden dat in de praktijk empirische formules worden gebruikt.

Hoe gaat het met de constante van Antoine?

Er is geen theoretische methode om de constanten van Antoine te verkrijgen, omdat het een empirische relatie is.

Ze worden verkregen uit de experimentele gegevens van elke stof en het aanpassen van de drie parameters A, B en C, zodat ze het kwadratische verschil (methode van de vierkante minima) van de voorspelling minimaliseren met de experimentele gegevens.

Voor de eindgebruiker, die over het algemeen chemische ingenieurs zijn, zijn er tabellen in de chemiehandleidingen waar deze constanten worden gegeven voor elke stof die de maximale en minimale temperatuurbereiken aangeven waarin ze van toepassing zijn.

Kan u van dienst zijn: Weerstandsthermometer: kenmerken, werking, gebruik

Online services zijn ook beschikbaar die de waarden van de constanten A, B en C geven, zoals het geval is van DDBST GMBH Onlines Services.

Voor dezelfde stof kan er meer dan één geldigheidstemperaturen zijn. Afhankelijk van het werkbereik wordt een of andere groep constanten gekozen.

De moeilijkheden kunnen verschijnen als het temperatuurwerkbereik tussen twee geldigheidsbereiken van de constanten ligt, omdat de formuledrukvoorspellingen niet samenvallen in de borderline -zone.

Voorbeelden

voorbeeld 1

Vind de waterdampdruk bij 25 ℃.

Oplossing 

We hebben de tafels geraadpleegd om de constanten van Antoine te bepalen.

Er zijn twee waterbereiken: 

Tussen 1 ℃ en 100 ℃ en tussen 99 ℃ tot 374 ℃.

Omdat we geïnteresseerd zijn in 25 ℃ nemen we het eerste bereik waarin de waarde van de constanten van Antoine is:

A = 8.07131

B = 1730.63

C = 233,426

P = 10^(8.07131 - 1730.63/(25 + 233,426)))

Berekening van de exponent

Laten we eerst de exponent berekenen: 1.374499

P = 10^1.374499 = 23.686 mmHg = 0,031166 ATM

Resultatenanalyse

Deze resultaten worden als volgt geïnterpreteerd:

Stel dat zuiver water wordt geplaatst in een hermetische container waaraan de lucht is geëxtraheerd door een vacuümpomp.

De container met water wordt in een thermisch bad geplaatst bij een temperatuur van 25 ℃ totdat het thermische evenwicht bereikt.

Water in de hermetische container verdampt gedeeltelijk totdat de verzadigingsdampdruk is bereikt, wat niets anders is dan de druk waarin de dynamische balans tussen de vloeibare fase van het water en de stoomfase wordt vastgesteld. 

Kan u van dienst zijn: Dirac Jordan Atomic Model: kenmerken en postulaten

Die druk bleek in dit geval 0,031166 atm te zijn bij 25 ℃.

Voorbeeld 2

Vind de waterdampdruk bij 100 ℃.

Oplossing 

We hebben de tafels geraadpleegd om de constanten van Antoine te bepalen. Er zijn twee waterbereiken: 

Tussen 1 ℃ en 100 ℃ en tussen 99 ℃ tot 374 ℃.

In dit geval ligt de interesse temperatuur in de twee reeksen.

We gebruiken de eerste van de bereiken [1 ℃, 100 ℃]

A = 8.07131

B = 1730.63

C = 233,426

P = 10^(8.07131 - 1730.63/(100 + 233,426)))

Berekening van de exponent

Laten we eerst de exponent berekenen: 2.8808

P = 10^1,374499 = 760,09 mmHg = 1.0001 atm

Vervolgens gebruiken we de tweede van de bereiken [99 ℃, 374 ℃]

In dit geval zijn de constanten dat

A = 8,14019

B = 1810.94

C = 244.485

P = 10^(8.14019 - 1810.94/(100 + 244.485))

Laten we eerst de exponent berekenen: 2.88324

P = 10^2.88324 = 764.2602 mmHg = 1.0056 ATM

Er is een procentuele verschil tussen de twee resultaten van 0,55%.

Referenties

1. Toepassing van de wetten van Raoult en Dalton en de Antoine -vergelijking. Opgehaald uit: mijn eigen en oude.WordPress.com
2.  Online rekenmachine van de Antoine -formule. Hersteld van: ddbonline.DDBST.van/antoinecalcion/antoinecalculaticgi.ETE
3. Gecousb. Thermodynamica en stoomtafels / constant van Antoine. Hersteld van: GECOUSB.com.gaan
4. Thermische eigenschappen van materie. Hersteld van: webserver.DMT.UPM.is
5. Gieren en yang. Antoine constante tabellen voor meer dan 700 organische verbindingen. Hersteld van: gebruiker.Eng.Umd.Edu
6. Wikipedia. Antoine -vergelijking. Hersteld van Wikipedia.com
7. Wikipedia. Clausius-Claapeyron-vergelijking. Hersteld van Wikipedia.com
8. Wisniak J. Historische ontwikkeling van de stoomdrukvergelijking van Dalton Toy Antoine. Hersteld van: link.Springer.com