Eindige vaste eigenschappen, voorbeelden, oefeningen opgelost

Het wordt begrepen door Eindige set allemaal ingesteld met een beperkt of boekhoudkundige aantal elementen. Voorbeelden van eindige sets zijn de knikkers die in een tas zijn opgenomen, de set huizen in een buurt of de set P Gevormd door de twintig (20) natuurlijke nummers:

P = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12,13, 14, 16, 17, 18, 19, 20 

De set universumsterren is zeker enorm, maar het is niet zeker bekend of het eindig of oneindig is. De set van planeten van het zonnestelsel is echter eindig.

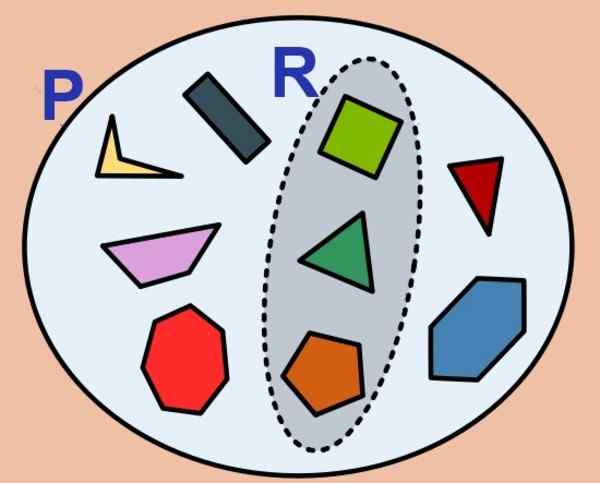
Figuur 1. De set polygonen is eindig en ook de subset van de reguliere. (Wikimedia Commons)

Het aantal elementen van een eindige set wordt de kardinaliteit genoemd en voor de set P Het wordt als volgt aangegeven: kaart (P) of #P. De lege set heeft nul kardinaliteit en wordt beschouwd als een eindige set.

[TOC]

Eigenschappen

Onder de eigenschappen van eindige sets zijn de volgende:

1- De unie van eindige sets resulteert in een nieuwe eindige set.

2- Als twee eindige set onderschept, is dit een nieuwe eindige set.

3- Een subset van een eindige set is eindig en de kardinaliteit is kleiner dan of gelijk aan die van de oorspronkelijke set.

4- De lege set is een eindige set.

Voorbeelden

Er zijn veel voorbeelden van eindige sets. Onder sommige voorbeelden zijn de volgende:

Set M van de maanden van het jaar, die als volgt kan worden verlengd:

M = Januari, februari, maart, april, mei, juni, juli, augustus, september, oktober, november, december, de kardinaliteit van m is 12.

Set S van de dagen van de week: S = Maandag, dinsdag, woensdag, donderdag, vrijdag, zaterdag, zondag. De kardinaliteit van S is 7.

Kan u van dienst zijn: evenredigheidsrelaties: concept, voorbeelden en oefeningen

Set N Uit de letters van het Spaanse alfabet is het een eindige set, deze ingestelde door uitbreiding is als volgt geschreven:

N = A, b, c, d, e, f, g, h, i, j, k, l, m, n, ñ, o, p, q, r, s, t, u, v, w, W, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, W, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, x, y, z en zijn Kardinaliteit is 27.

Set V Uit de klinkers in het Spaans is het een subset van de set:

V ⊂ N Daarom is het een eindige set.

De eindige set V Uitgebreide manier waarop het zo is geschreven: V = a, e, i, o, u en de kardinaliteit is 5.

Sets kunnen worden uitgedrukt door begrip. Set F Gemaakt uit de letters van het woord "eindig" is een voorbeeld:

F = x / x is een letter van het woord "eindig"

Deze set uitgedrukt zal uitgebreid zijn:

F = f, i, n, t, o waarvan de kardinaliteit 5 is en daarom is het een eindige set.

Meer voorbeelden

De kleuren van de regenboog zijn een ander eindig set voorbeeld, de set C van deze kleuren is:

C = rood, oranje, geel, groen, cyaan, blauw, violet en de kardinaliteit is 7.

De set fasen F Van de maan is een ander eindig set voorbeeld:

F = Nieuwe maan, groeieruimte, volle maan, afnemende kamer Deze set heeft kardinaliteit 4.

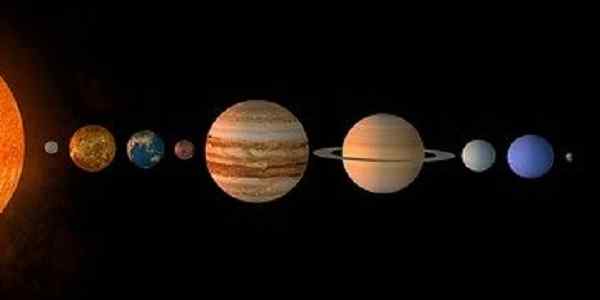Figuur 2. De planeten van het zonnestelsel vormen een eindige set. (Pixabay)

Een andere eindige set is die gevormd door de planeten van het zonnestelsel:

P = Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, Neptunus, Pluto Cardinality 9.

Opgeloste oefeningen

Oefening 1

De volgende set wordt gegeven a = x∊ r / x^3 = 27. Druk het uit in woorden en schrijf het bij uitbreiding, duiden op de kardinaliteit en zeg of het wel of niet eindig is.

Kan u van dienst zijn: ellips

Oplossing: Set A is de set reële getallen x zodanig dat X daardoor naar de kubus is verhoogd 27.

Vergelijking x^3 = 27 heeft drie oplossingen: die x1 = 3, x2 = (-3/2 + 3√3/2 i) en x3 = (-3/2-3√3/2 i). Van de drie oplossingen is alleen X1 echt, terwijl de andere twee complexe nummers zijn.

Omdat de definitie van set A zegt dat X tot reële getallen behoort, zijn oplossingen in complexe getallen geen deel uit.

De uitgebreide set is:

A = 3, wat een eindige set kardinaliteit is 1.

Oefening 2

Schrijf symbolisch (door begrip) en uitgebreid de set B van de reële getallen die groter zijn dan 0 (nul) en minder of gelijk dan 0 (nul). Geef uw kardinaliteit aan en of deze al dan niet eindig is.

Oplossing: B = x∊ r / 0 < x <= 0

Set B is leeg omdat een reëel getal x niet gelijktijdig groter en minder dan nul kan zijn, evenals 0 en ook minder dan 0.

B = en de kardinaliteit is 0. De lege set is een eindige set.

Oefening 3

De s set van de oplossingen van een bepaalde vergelijking wordt gegeven. De set van begrip is als volgt geschreven:

S = x∊ r / (x -3) (x^2 - 9x + 20) = 0

Schrijf deze set uitgebreid, geef je kardinaliteit aan en geef aan of het een eindige set is of niet.

Oplossing: Ten eerste, door de uitdrukking te analyseren die de set s beschrijft, wordt verkregen dat het een set echte X -waarden is die oplossingen van de vergelijking zijn:

(x -3) (x^2 - 9x + 20) = 0 (*)

Een oplossing van deze vergelijking is x = 3, wat een reëel getal is en daarom tot S behoort. Maar er zijn meer oplossingen die kunnen worden verkregen op zoek naar de oplossingen van de kwadratische vergelijking:

Kan u van dienst zijn: Distributie F: Kenmerken en oefeningen opgelost

(x^2 - 9x + 20) = 0

De vorige uitdrukking kan als volgt factor zijn:

(x - 4) (x - 5) = 0

Dat leidt ons naar nog twee oplossingen van de oorspronkelijke (*) vergelijking die x = 4 en x = 5 zijn. Kortom, vergelijking (*) heeft oplossingen 3, 4 en 5.

De S -set die uitgebreid wordt uitgedrukt, is als volgt:

S = 3, 4, 5, die Cardinality 3 heeft en daarom een ​​eindige set is.

Oefening 4

Er zijn twee sets a = 1, 5, 7, 9, 11 en b = x ∊ n / x is par ^ x x < 10 .

Schrijf Set B expliciet en vind de Unie met de set A. Vind ook de onderschepping van deze twee sets en concludeer.

Oplossing: Set B bestaat uit natuurlijke getallen zodanig dat ze zelfs zijn en ook lager zijn dan waarde 10, daarom wordt B -uitgebreid samen als volgt geschreven:

B = 2, 4, 6, 8

De unie van set A met set B is:

A u b = 1, 2, 4, 5, 6, 7, 8, 9, 11

En de onderschepping van set A met set B is als volgt geschreven:

A ⋂ b = = Ø is de lege set. 

Opgemerkt moet worden dat de unie en onderschepping van deze twee eindige sets leiden tot nieuwe sets, die op hun beurt ook eindig zijn.

Referenties

1. Bronnen, een. (2016). BASIS WISKUNDE. Een inleiding tot berekening. Lulu.com.
2. Garo, m. (2014). Wiskunde: kwadratische vergelijkingen: hoe een kwadratische vergelijking oplossen. Marilù Garo.
3. Haeussler, E. F., & Paul, r. S. (2003). Wiskunde voor administratie en economie. Pearson Education.
4. Jiménez, J., Rodríguez, m., Estrada, r. (2005). Wiskunde 1 september. Drempelwaarde.
5. Kostbaar, c. T. (2005). Wiskundecursus 3o. Redactionele progreso.
6. Wiskunde 10 (2018). "Voorbeelden van eindige sets". Opgehaald uit: Mathematics10.netto
7. Rock, n. M. (2006). Algebra I is gemakkelijk! Zo makkelijk. Team Rock Press.
8. Sullivan, J. (2006). Algebra en trigonometrie. Pearson Education.
9. Wikipedia. Eindige set. Hersteld van: is.Wikipedia.com