Bose Einstein condensaat
- 4883
- 560
- Glen Armstrong
We leggen uit wat het Bose-Einstein-condensaat is, zijn oorsprong, kenmerken, hoe het wordt verkregen en zijn toepassingen
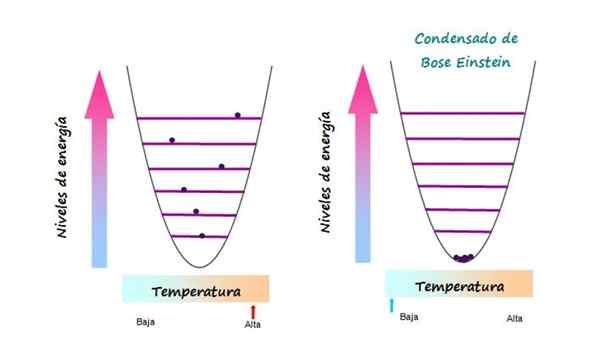
Figuur 1.- In het condensaat van Bose Einstein worden op de laagste energietoestand op lage temperatuur allemaal gehandhaafd. Bron: f. Zapata Wat is het condensaat van Bose Einstein?
Bose Einstein's condensaat (CBE) is een staat van aggregatie van materie, evenals de gebruikelijke staten: gasvormige, vloeistof en vast.
Het bestaat uit deeltjes die bosonen worden genoemd, die zich bij deze temperaturen bevinden in de kwantumstaat van lagere energie, genaamd Fundamentele staat. Albert Einstein voorspelde deze omstandigheid in 1924, na het lezen van de werken die door de hindoeïstische natuurkundige Satyendra Bose waren gestuurd over de statistieken van de fotonen.
Het is niet eenvoudig om in het laboratorium de noodzakelijke temperaturen te verkrijgen voor de vorming van het Bose-Einstein-condensaat, dus moesten we wachten tot 1995 om de nodige technologie te hebben.
Dat jaar slaagden de Amerikaanse fysici Eric Cornell en Carl Wieman (Universiteit van Colorado) en vervolgens de Duitse natuurkundige Wolfgang Ketterle (MIT), erin het eerste condensaat van Bose-Einstein te observeren. Colorado-wetenschappers gebruikten Rubidio-87, terwijl Ketterle het bereikte door een extreem verdund gas van natriumatomen.
Dankzij deze experimenten, die de deuren openden voor nieuwe onderzoeksvelden in de aard van het onderwerp, ontvingen Ketterle, Cornell en Wieman de Nobelprijs in 2001.
En het is dat de zeer lage temperaturen het mogelijk maken dat de atomen van een gas met bepaalde kenmerken zo'n ordelijke toestand worden uitgevoerd, dat ze erin slagen om dezelfde verminderde energie en hoeveelheid beweging te verwerven, iets dat niet in gewone materie gebeurt.
Bose-Einstein condensaatkenmerken
Laten we eens kijken naar de belangrijkste kenmerken van het Bose-Einstein-condensaat:
- Bose-Einstein-condensaat wordt geproduceerd in gassen die bestaan uit zeer verdunde bosonische atomen.
- De atomen in het condensaat blijven in dezelfde kwantumtoestand: de fundamentele of lagere energietoestand.
- Extreem lage temperaturen zijn vereist, alleen wat nano-kelvin boven de absolute nul. Hoe lager de temperatuur, het golfgedrag van de deeltjes wordt steeds vaker duidelijk.
- In principe bestaat materie in de Bose Einstein -condensaatstatus niet in de natuur, omdat tot op heden temperaturen niet onder 3 k zijn gedetecteerd.
- Sommige CBE hebben supergeleiding en super-fluïditeit, dat wil zeggen gebrek aan oppositie tegen de passage van de huidige, evenals viscositeit.
- De atomen in het condensaat, allemaal in dezelfde kwantumtoestand, presenteren uniformiteit in hun eigenschappen.
Oorsprong van het Bose-Einstein-condensaat
Wanneer je een gas hebt vergrendeld in een container, houden de deeltjes die het samenstellen, houden voldoende afstand van elkaar, interactie zeer weinig, behalve incidentele botsingen tussen hen en met de wanden van de container. Van daaruit ontleent het goed bekende ideale gasmodel.
De deeltjes bevinden zich echter in een permanente thermische agitatie en de temperatuur is de beslissende parameter die de snelheid definieert: bij een hogere temperatuur, snellere beweging.
En hoewel de snelheid van elk deeltje kan variëren, blijft de gemiddelde snelheid van het systeem constant bij een gegeven temperatuur.
Fermions en bosonen
Het volgende belangrijke feit is dat materie bestaat uit twee soorten deeltjes: fermionen en bosonen, gedifferentieerd door spin (intrinsiek hoekmomentum), een volledig kwantumkwaliteit.
Het elektron is bijvoorbeeld een fermion met semi-bestaande spin, terwijl bosonen hele spin hebben, waardoor hun statistisch gedrag anders is.
Fermions zijn graag anders en gehoorzamen daarom het uitsluitingsprincipe van Pauli, volgens welke er geen twee fermionen in het atoom kunnen zijn met dezelfde kwantumtoestand. Dit is de reden waarom de elektronen zich in verschillende atomaire orbitalen bevinden en dus niet dezelfde kwantumstaat bezetten.
Aan de andere kant houden bosonen zich niet aan het principe van uitsluiting, dus hebben ze geen ongemak om dezelfde kwantumstaat te bezetten.
Dubbele aard van materie
Een ander belangrijk feit in het begrip van de CBE is de dubbele aard van de zaak: golf en deeltjes tegelijkertijd.
Zowel fermionen als bosonen kunnen worden omschreven als een golf met een bepaalde uitbreiding in de ruimte. De golflengte λ van deze golf is gerelateerd aan zijn momentum of hoeveelheid beweging P, Door de vergelijking van de Broglie:
Kan u van dienst zijn: elektrodynamica
Waar H de constante van Planck is, waarvan de waarde 6.62607015 × 10 is-3. 4 J.S.
Bij hoge temperaturen overheerst de thermische agitatie, wat betekent dat het momentum P is groot en golflengte λ is klein. Atomen tonen dus hun eigenschappen als deeltjes.
Maar wanneer de temperatuur daalt, neemt de thermische agitatie af en daarmee het momentum, dat is ontstaan dat de golflengte toeneemt en de golvende kenmerken prevaleren. Aldus houden de deeltjes op zich te vinden, omdat de respectieve golven hun grootte verhogen en met elkaar overlappen.
Er is een bepaalde kritieke temperatuur waaronder de bosonen in de fundamentele staat zijn, die de staat is met de laagste energie (het is niet 0). Dat is wanneer er condensatie optreedt.
Het resultaat is dat bosonische atomen niet langer te onderscheiden zijn en het systeem een soort superatoom wordt, beschreven door een enkele golffunctie. Het is gelijk aan het zien door een krachtige toename -lens waarmee u de details kunt zien.
Hoe kom je aan het condensaat?
De moeilijkheid van het experiment ligt om het systeem op voldoende lage temperaturen te houden, zodat de golflengte van De Broglie hoog blijft.
Colorado -wetenschappers bereikten het via een laserkoelsysteem, dat bestaat uit het frontaal van het atoommonster met zes laserlichtstralen om ze scherp te stoppen en dus hun thermische agitatie drastisch te verminderen.
Toen werden de koudere en langere atomen gevangen door een magnetisch veld, waardoor het snelst het systeem verder koelt.
Kan u van dienst zijn: Kirchhoff -wetten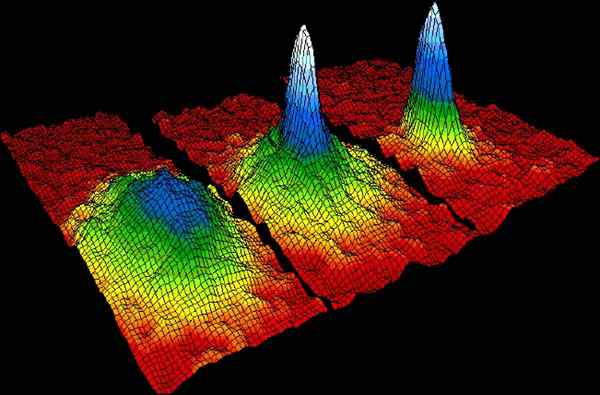
Figuur 2.- Snelheidsverdeling van RB -atomen in de CBE. De witte piek vertegenwoordigt het grootste aantal atomen, met geschatte snelheid van 0.5 mm/s. Bron: Wikimedia Commons. De op deze manier beperkte atomen slaagden erin om een paar ogenblikken een kleine druppel CBE te vormen, die voldoende tijd duurde om in een afbeelding te worden opgenomen.
Toepassingen en voorbeelden
CBE -applicaties zijn momenteel in volledige ontwikkeling en zullen nog wat tijd doorbrengen.
Kwantum computing
Het handhaven van samenhang in kwantumcomputers is geen gemakkelijke taak, dus CBE is voorgesteld als een middel om de uitwisseling van informatie tussen individuele kwantumcomputers te behouden.
Vermindering van lichtsnelheid
De snelheid van het licht in vacuüm is een constante van de natuur, hoewel de waarde ervan in andere media, zoals in water, anders kan zijn.
Dankzij de CBE is het mogelijk om de snelheid van het licht grotendeels te verminderen, tot 17 m/s, volgens sommige experimenten. Dit is iets dat niet alleen meer kan verdiepen in de studie van de aard van het licht, maar het gebruik ervan in Quantum Computing om informatie op te slaan.
Atomaire horloges van grote precisie
Koude atomen maken het maken van atomaire horloges van grote precisie mogelijk, die minimale vertragingen ervaren in lange periodes, in de orde van miljoenen jaren, zeer nuttige kwaliteiten bij het synchroniseren van GPS -systemen.
Simulatie van kosmologische processen
De atomaire krachten die in het condensaat worden gegenereerd, kunnen helpen de omstandigheden te simuleren waarin fysieke processen plaatsvinden binnen enkele opmerkelijke objecten in het universum, zoals neutronensterren en zwarte gaten.
Referenties
- Bauer, W. 2011. Fysica voor engineering en wetenschappen. Deel 1. MC Graw Hill.
- Chang, R. 2013. Scheikunde. Elfde editie. McGraw Hill Education.
- Landsil. De vijf staten van materie. Hersteld van: Landsil.com.
- Het qubit -rapport. Bose-Einstein condensaatvormingssnelheid nam toe, de vormingsmethode vereenvoudigd. Opgehaald uit: qubitreport.com.
- Tipler, p. 2008. Moderne fysica. 5e. Bewerking. W. H. Freeman & Company.