Samenvoegbaarheid van vaste stoffen, vloeistoffen, gassen, voorbeelden

De samendrukbaarheid van een stof of materiaal is de verandering in volume die het ervaart wanneer het onderhevig is aan een drukverandering. Meestal neemt het volume af bij het uitoefenen van een druk op een systeem of object. Soms komt het tegenovergestelde echter voor: een drukverandering kan een explosie veroorzaken waarin het systeem het volume verhoogt, of wanneer een faseverandering plaatsvindt.

In sommige chemische reacties kan dit gebeuren en ook in gassen, omdat door de frequentie van botsingen te verhogen, de afstotende krachten plaatsvinden.

Een onderzeeër ervaart compressiekrachten wanneer ondergedompeld. Bron: Pixabay.com.

Door zich voor te stellen hoe gemakkelijk of moeilijk het kan zijn om een ​​object te comprimeren, moet u rekening houden. In elk van hen houden de moleculen bepaalde afstanden van elkaar. Hoe stevig de links die de middelenmoleculen verenigen die het object en dichterbij vormen, hoe moeilijker het is om een ​​vervorming te veroorzaken.

Een vaste stof heeft zijn zeer nauwe moleculen, en bij het proberen meer, verschijnen afstotingskrachten die de taak belemmeren. Daarom wordt gezegd dat vaste stoffen niet compressief zijn. In vloeibare moleculen is er meer ruimte, dus de samendrukbaarheid is groter, maar toch vereist de verandering in volume meestal grote krachten.

Dus vaste stoffen en vloeistoffen zijn nauwelijks samendrukbaar. Een zeer grote drukvariatie zou nodig zijn om een ​​aanzienlijke verandering te bereiken in de zogenaamde normale druk- en temperatuuromstandigheden. Aan de andere kant worden gassen, omdat ze zeer afstandelijke moleculen hebben, gemakkelijk gecomprimeerd en gedecomprimeerd.

[TOC]

Solide samendrukbaarheid

Wanneer een object bijvoorbeeld in een vloeistof wordt ondergedompeld, oefent het druk uit op het object in alle richtingen. Op deze manier kunnen we denken dat het volume van het object zal afnemen, hoewel dit in de meeste gevallen niet merkbaar zal zijn.

De situatie is te zien in de volgende figuur:

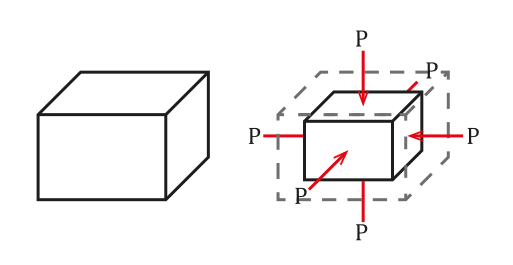De kracht die wordt uitgeoefend door de vloeistof op het ondergedompelde object staat loodrecht op het oppervlak. Bron: Wikimedia Commons.

De druk wordt gedefinieerd als kracht per oppervlakte -eenheid, die een volumeverandering zal veroorzaken ΔV die evenredig is aan het initiële volume van object V_of. Deze volumeverandering hangt af van de kwaliteiten van hetzelfde.

De wet van Hooke stelt dat de vervorming van een object evenredig is met de op de toegepaste inspanning:

Inspanning ∝ vervorming

De volumetrische vervorming die door een lichaam wordt ervaren, wordt gekwantificeerd door B de vereiste evenredigheidsconstante, die wordt genoemd als de Volumetrische module van het materiaal:

B = -Seft/unitaire vervorming

Kan u van dienst zijn: thermische straling: eigenschappen, voorbeelden, toepassingen

B = -AP/ (ΔV/ V_of))

Zoals ΔV/v_of Het is een dimensieloze hoeveelheid, omdat het het quotiënt is tussen twee delen, de volumetrische module heeft dezelfde drukeenheden, die in het internationale systeem Pascal zijn (PA).

Het negatieve teken geeft de verwachte volume -vermindering aan, wanneer het object voldoende wordt gecomprimeerd, dat wil zeggen, de druk neemt toe.

-Samendrukbaarheid van een materiaal

De omgekeerde of wederzijdse waarde van de volumetrische module staat bekend als samendrukbaarheid En het wordt aangeduid met de teksten k. Daarom:

Hier k Het is het negatieve van de fractionele volumeverandering als gevolg van toename van de druk. De eenheden in het internationale systeem zijn het omgekeerde van de PA, dat is m² /N.

De vergelijking voor B of K indien voorkeur, is van toepassing op zowel vaste stoffen als vloeistoffen. Het volumetrische module -concept wordt zelden toegepast op gassen. Later wordt een eenvoudig model uitgelegd om de afname van het volume te kwantificeren dat een echt gas kan ervaren.

De snelheid van het geluid en de compressibiliteitsmodule

Een interessante toepassing is de snelheid van het geluid in een medium, die afhankelijk is van de compressibiliteitsmodule van hetzelfde:

Waar C de snelheid van het geluid is, is B de volumetrische module en ρ is de dichtheid van het medium

Opgeloste oefeningen-voorbeelden

-Oefening opgelost 1

Een solide koperen bol waarvan het volume 0 is.8 m³ Het valt in de oceaan tot een diepte waarin de hydrostatische druk 20 m groter is dan op het oppervlak. Welke verandering zal het volume van de bol ervaren? Het is bekend dat de messing compressibiliteitsmodule is B = 35.000 MPa,

Oplossing

1 M PA = 1 Mega Pascal = 1. 10 ⁶ vader

De drukvariatie ten opzichte van het oppervlak is dp = 20 x 10 ⁶ vader. Door de gegeven vergelijking voor B toe te passen, hebt u:

B = -AP/ (ΔV/ V_of))

Daarom:

Dus:

ΔV = -5.71.10 ^-4 X 0.8 m³ = -4.57 x 10^-4 M³

Het volumeverschil kan een negatief teken hebben wanneer het uiteindelijke volume kleiner is dan het initiële volume, daarom komt dit resultaat overeen met alle veronderstellingen die we tot nu toe hebben gemaakt.

De compressibiliteitsmodule zo hoog, geeft aan dat een grote verandering in de druk vereist is, zodat het object een aanzienlijk volume -afname ervaart.

-Oefening opgelost 2

Het oor tegen de treinsporen plaatsen is bekend wanneer een van deze voertuigen in de verte nadert. Hoe lang duurt het geluid als het door een stalen rail reist als de trein op 1 km afstand is?

Kan u van dienst zijn: behoud van het lineaire momentum: principe, voorbeelden, oefeningen.

Gegevens

Stalen dichtheid = 7.8 x 10 ³ kg/m3

Stalen samendrukbaarheidsmodule = 2.0 x 10 ^elf vader.

Oplossing

Samperrukbaarheid van vloeistoffen

De hierboven berekende compressibiliteitsmodule B wordt ook toegepast op vloeistoffen, hoewel meestal een grote inspanning nodig is om een ​​aanzienlijke afname van het volume te produceren. Maar vloeistoffen kunnen uitbreiden of samentrekken als ze verwarmen of afkoelen, en ook als ze worden ontmoedigd of onder druk gezet.

Voor water in standaarddruk- en temperatuuromstandigheden (0 ºC en een drukatmosfeer ongeveer of 100 kPa), is de volumetrische module 2100 MPa. Dat wil zeggen, ongeveer 21000 keer atmosferische druk.

Daarom worden in de meeste toepassingen vloeistoffen meestal als niet -samendrukbaar beschouwd. Dit is onmiddellijk te zien met numerieke toepassing.

-Oefening opgelost 3

Zoek de fractionele afname van het watervolume wanneer onderworpen aan een druk van 15 MPa.

Oplossing

Samperrukbaarheid in gassen

Gassen, zoals hierboven uitgelegd, werken een beetje anders.

Om te weten welk volume ze hebben N mol een bepaald gas wanneer het bij een druk wordt beperkt P en bij een temperatuur T, De staatsvergelijking wordt gebruikt. In de staatsvergelijking voor een ideaal gas, waar geen intermoleculaire krachten in aanmerking worden genomen, geeft het eenvoudigste model aan dat:

P.V_ideaal = n. R. T

Waar r de constante van ideale gassen is.

Veranderingen in gasvolume kunnen worden uitgevoerd bij constante druk of bij constante temperatuur. Door bijvoorbeeld de temperatuur constant te houden, is de isotherme samendrukbaarheid κ_T is:

In plaats van het "delta" -symbool dat werd gebruikt voordat het concept voor vaste stoffen werd gedefinieerd, wordt het voor een gas beschreven met afgeleide, in dit geval gedeeltelijk afgeleid met betrekking tot P, met behoud van constante t.

Daarom B_T De isothermische samendrukbaarheidsmodule is:

 B_T = P

En de adiabatische module B -module B is ook belangrijk_adiabatisch, Waarvoor er geen inkomende of uitgaande warmtestroom is.

B_adiabatisch = γp

Waarbij γ de adiabatische coëfficiënt is. Met deze coëfficiënt kunt u de geluidssnelheid in de lucht berekenen:

-Oefening opgelost 4

Door de vorige vergelijking toe te passen, vindt u de snelheid van het geluid in de lucht.

Gegevens

De adiabatische luchtcompressibiliteitsmodule is 1,42 × 10⁵ vader

Luchtdichtheid is 1.225 kg/m³ (bij atmosferische druk en 15 ºC)

Oplossing

De samendrukbaarheidsfactor z

In plaats van te werken met de compressibiliteitsmodule, als een volume -eenheid van volume als gevolg van drukverandering, de ECHTE GAS SOMPRESSIBRIEK Factor, Een ander maar illustratief concept over hoe echt gas zich verhoudt tot het ideale gas:

Kan u van dienst zijn: golvende lichttheorie: uitleg, toepassingen, voorbeelden

P . V_echt = Z. R. T

Waarbij z de consisbosbaarheid van gaskruisbaarheid is, die afhangt van de omstandigheden waaronder het is, meestal een functie van zowel de P- als de temperatuur T -druk, kunnen zich uitdrukken als:

Z = f (p, t)

In het geval van een ideaal gas z = 1. Voor echte gassen neemt de Z -waarde bijna altijd toe met druk en neemt af met de temperatuur.

Door de druk te verhogen, botsen gasvormige moleculen vaker vaker en zijn de afstotende krachten tussen hen verhoogd. Dit kan leiden tot een toename van het volume in echt gas, dus z> 1.

Aan de andere kant, om de druk te verlagen, zijn de moleculen vrij om te bewegen en de krachten van aantrekkingskracht overheersen. In dit geval, z < 1.

Voor het eenvoudige geval van 1 mol gas n = 1, als dezelfde druk- en temperatuuromstandigheden worden gehandhaafd, worden de vorige vergelijkingen verkregen door de vorige vergelijkingen te delen:

Er wordt geconcludeerd dat:

V_echt = Z V_ideaal

-Oefening opgelost 5

Er is een echt gas bij 250 ºK en 15 atm druk, dat een molair volume heeft dat 12 % lager is dan dat berekend door de status van ideale gassen. Als de druk en temperatuur constant blijven, zoek dan:

a) de samendrukbaarheidsfactor.

b) Het molaire volume van echt gas.

c) Wat voor soort krachten overheersen: aantrekkelijk of weerzinwekkend?

Oplossing

a) Als het echte volume 12 % lager is dan het ideaal, betekent dit dat:

V_echt = 0.88 V_ideaal

Daarom is de samendrukbaarheidsfactor voor 1 mol gas:

Z = 0.88

b) Het kiezen van de constante van de ideale gassen met de juiste eenheden voor de verstrekte gegevens:

R = 0,082 l.ATM/MOL.K

Het molaire volume wordt berekend door waarden te wissen en te vervangen:

c) Aantrekkelijke krachten overheersen, omdat Z minder is dan 1.

Referenties

1. Atkins, P. 2008. Fysische chemie. Pan -Amerikaans medisch redactioneel. 10 - 15.
2. Giancoli, D.  2006. Fysica: principes met toepassingen. 6^e. Ed Prentice Hall. 242 - 243 en 314-15
3. Mott, r.  2006. Vloeistofmechanica. Pearson Education.13-14.
4. Rex, a. 2011. Fundamentals of Physics. Pearson Education. 242-243.
5. Tipler, p. (2006) Natuurkunde voor wetenschap en technologie. 5e ed. Deel 1. Redactioneel teruggekeerd. 542.