Poisson -coëfficiëntcoëfficiënt, formules, waarden, voorbeelden

Hij Poisson -coëfficiënt Het is een dimensieloze hoeveelheid, kenmerkend voor elk materiaal. Het is een indicatie van de vervorming van een stuk materiaal vóór de toepassing van bepaalde inspanningen.

Wanneer een materiaalstuk dat spanning of compressie ondergaat, een vervorming lijdt, is het quotiënt tussen transversale vervorming en longitudinale vervorming precies de Poisson -coëfficiënt.

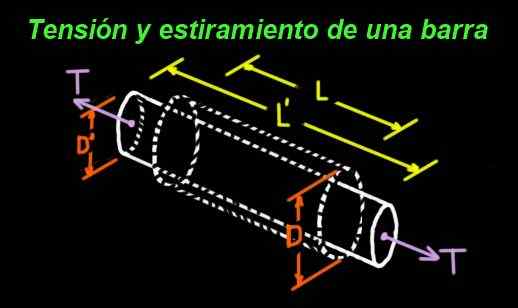
Figuur 1. Poisson's coëfficiënt meet de relatie tussen longitudinaal stretchen en dwars vernauwing. (Opgesteld door Ricardo Pérez)

Een rubberen cilinder die spanning aan de uiteinden ondergaat, wordt bijvoorbeeld in longitudinale richting uitgerekt, maar deze is transversaal smal. Figuur 1 toont een balk waarvan de oorspronkelijke afmetingen zijn: lange l en diameter d.

De balk wordt door zijn uiteinden onderworpen aan een T -spanning, en als gevolg van deze spanning lijdt een stuk, zodat de nieuwe lengte l '> l is. Maar bij het uitrekken komt ook een vernauwing van de diameter van de nieuwe waarde voor: D ' < D.

Het quotiënt tussen stretching (positief) en vernauwing (negatief) vermenigvuldigd met (-1), is een positief getal tussen 0 en 0,5. Dit nummer is de zo -aangedane Poisson ν -coëfficiënt (Griekse brief).

[TOC]

Poisson -coëfficiëntformule

Om de Poisson -coëfficiënt te berekenen, is het noodzakelijk om de longitudinale en transversale eenheid vervorming te bepalen.

Longitudinale eenheid vervorming ε_L Het is het stuk verdeeld tussen de oorspronkelijke lengte:

ε_L = (L ' - l) / l

Evenzo, transversale unitaire vervorming ε_T Het is de radiale vernauwing verdeeld tussen de oorspronkelijke diameter:

ε_T = (D ' - d) / d

Daarom wordt de Poisson -coëfficiënt berekend door de volgende formule:

ν = - ε_T / ε_L 

Relatie met de elasticiteitsmodule en de stijfheidsmodule

Poisson ν coëfficiënt is gerelateerd aan de module EN van elasticiteit (of jonge module) en met de rigiditeitsmodule G, door de volgende formule:

Kan u van dienst zijn: Geometrische optiek: welke studies, wetten, toepassingen, oefeningen

ν = e /(2g) - 1

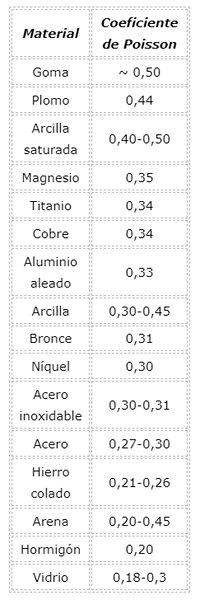
Poisson -coëfficiëntwaarde voor materialen

Figuur 2. Roestvrij staal heeft Poisson -coëfficiënt tussen 0,30 en 0,31. Bron: Pixabay.

Voorbeelden van berekening

voorbeeld 1

Een balk van een bepaald plastic materiaal heeft een lengte van 150 mm en een cirkelvormige sectie met een diameter van 20 mm. Wanneer een compressiekracht van 612,25 kg-F wordt onderworpen aan een compressiekracht, wordt een verkorting van 14 mm waargenomen en tegelijkertijd een toename van 0,85 mm in de diameter van de balk.

Berekenen:

a) Longitudinale unitaire vervorming.

b) Transversale unitaire vervorming.

c) Poissons coëfficiënt van dat materiaal.

d) De elasticiteitsmodule van de jongeren die overeenkomt met het materiaal.

e) De stijfheidsmodule voor dat plastic.

Oplossing voor

Bedenk dat de vervorming van de longitudinale eenheid εl de stretch is gedeeld door de oorspronkelijke lengte:

εl = (l ' - l) / l

εl = (-14 mm) / 150 mm = -0.0933

Merk op dat de longitudinale unitaire vervorming dimensieloos is en in dit geval heeft het negatief gegeven omdat er een afname van zijn longitudinale dimensie was.

Oplossing B

Evenzo is eenheidsovereenkomst van eenheidsovereenkomst εt radiaal vernauwing, gedeeld door de oorspronkelijke diameter:

εt = (d ' - d) / d

εt = (+0,85 mm) / 20 mm = 0,0425

Transversale unitaire vervorming is positief omdat de diameter van de bar een toename is geweest.

Oplossing C

Voor de berekening van Poisson -coëfficiënt moeten we niet vergeten dat het wordt gedefinieerd als het negatieve van het quotiënt tussen transversale vervorming en longitudinale vervorming:

ν = - εt / εl 

ν = - 0,0425 / (-0.0933) = 0.4554

Er moet aan worden herinnerd dat de coëfficiënt van Poisson een positief dimensieloze getal is en voor de meeste materialen is het tussen 0 en 0,5.

Kan u van dienst zijn: Darcy Law

Oplossing D

Young's elasticiteitsmodule, aangeduid met brief E, is de evenredigheidsconstante in de wet van Hooke. Door E is de normale inspanning σl gerelateerd aan de unitaire vervorming εl, als volgt:

σl = e εl 

Normale inspanning wordt gedefinieerd als het quotiënt tussen de normale kracht (in dit geval parallel aan de as van de balk) en de dwarsdoorsnede:

σl = f / a = f / (π / 4 * d^2)

In deze oefening is Force F 612,25 kg-F, die zal worden gemaakt aan Newtons die de eenheid van geweld is:

F = 612.25 kg-f = 612.25 * 9,8 n = 6000 n = 6 kN

Van zijn kant is de dwarsdoorsnede A:

A = (π/4 * d^2) = (3.1416/4) * (20 * 10^-3 m)^2 = 3.1416 * 10^-4 m^2

Eindelijk is de normale inspanning die op de bar wordt toegepast:

σl = f / a = 6000 n / 3,1416 * 10^-4 m^2 = 19.098.593 PA = 19.098 MPA

Om de elasticiteitsmodule van de jongeren te berekenen, wissen we en van de wet van hooke σl = e εl:

E = σl / εl = 19.098.593 PA / 0.0933 = 204.7 MPA

Oplossing e

De r -rigiditeitsmodule is gerelateerd aan de EG -module van Young en de Poisson ν -coëfficiënt door deze formule:

E / (2 g) = 1 + ν 

Van daaruit kunt u G:

G = E / (2 (1 + ν)) = 204.7 MPa / (2 (1 + 0.4554)) = 70,33 MPa

Voorbeeld 2

Je hebt een kabel met 4 mm en 1 m lange diameter. Wetende dat de Copper Young-module 110000 MPa is en dat de Poisson-coëfficiënt 0,34 is, schat het uitrekken en beperken in diameter dat de draad lijdt wanneer een gewicht van 100 kg-F.

Oplossing

In de eerste plaats is het noodzakelijk om de normale tractie -inspanning te berekenen die het gewicht uitoefent op de draad, volgens deze formule:

Kan u van dienst zijn: vectoren in de ruimte: hoe u kunt grafieken, toepassingen, oefeningen

σl = f / a = f / (π / 4 * d^2)

De kracht f is 980 N en de dwarsdoorsnede is:

A = (π/4 * d^2) = (3.1416/4) * (4 * 10^-3 m)^2 = 1.2566 * 10^-5 m^2

Dan is de tractie -inspanning:

σl = 980 n / 1,2566 * 10^-5 m^2 = 77.986.000 PA

Berekening van de vervorming van unitaire draad

De elasticiteitsmodule van de jongeren, aangeduid met letter E, is de evenredigheidsconstante in de wet van Hooke die de normale inspanning σl relateert aan de unitaire vervorming εl:

σl = e εl 

Van daaruit kan de longitudinale unitaire vervorming van de koperdraad worden gewist:

εl = σl / e = 77.986 MPA / 110000 MPa = 7,09 * 10^-4

Berekening van transversale eenheidsvervorming

Aan de andere kant, om de transversale unitaire vervorming te kennen, wordt de Poisson -coëfficiënt toegepast:

ν = - εt / εl 

Ten slotte moet je een transversale unitaire vervorming zijn: 

εt = -ν εl = -0.34 * 7.09 * 10 ^-4 = -2,41 * 10 ^-4

Kabel absolute rekberekening

Ten slotte moet de volgende relatie worden toegepast om het absolute uitrekken van de kabel te kennen:

Δl = εl * l = 7,09 * 10^-4 * 1 m = 7,09 * 10^-4 m = 0,709 mm

Dat wil zeggen, met dat gewicht strekte de kabel nauwelijks 0,709 millimeter uit.

Berekening van de afname van de diameter

Om absolute krimpende diameter te verkrijgen, gebruiken we de volgende formule:

Δd = εt * d = -2,41 * 10 ^-4 * 4 mm = -9,64 * 10 ^-4 mm = -0.000964 millimeter.

Deze vernauwing in de diameter is zo klein dat het moeilijk is om te waarderen met het blote oog, zelfs de meting vereist een instrument met een hoog precisie -instrument.

Referenties

1. Bier f ... materiële mechanica. 5e. Editie. 2010. MC Graw Hill. 1-130.
2. Hibbeler R. Materiaalmechanica. Achtste editie. Prentice Hall. 2011. 3-60.
3. Gere J. Materiaalmechanica. Achtste editie. Cengage leren. 4-220.
4. Giancoli, D. 2006. Fysica: principes met toepassingen. 6e ed. Prentice Hall. 238-242.
5. Valera Negrete, J. 2005. ALGEMENE FYSICA -NOTIES. UNAM. 87-98.